
K dokonalejšímu pochopení závislosti ceny opce na pohybu podkladového aktiva vyjádřeného řeckým písmenem Delta, jak jsem jej popisoval v článku Delta je zapotřebí hlubšího ponoru do problematiky řeckých písmen, když tím nejbližším písmenem k popisované Delta je řecké písmeno Gamma. Tak jako Rumburak byl čaroděj druhé kategorie, tak také na Gamma můžeme pohlížet jako na řecké písmeno „druhé kategorie“. Proč taková degradace? Popisoval jsem dříve, že cenu opcí vypočítávají matematické modely, kde nejznámější z nich – Black-Scholesův model, využívá při stanovení ceny opčních kontraktů šest základních údajů – Cenu podkladového aktiva, Hodnotu strike, Délku života opčního kontraktu, Implied Volatilitu, současnou Úrokovou míru a hodnotu případně vyplácené Dividendy za dobu života opce. Protože z těchto šesti údajů můžeme Hodnotu strike, Úrokovou míru a zjištění, zda se vyplácí Dividenda, brát jako zjištěné konstanty, potom nám cenu opčního kontraktu určují zbylé tři neznámé, které můžeme pozorovat a přemýšlet o míře jejich vlivu na cenu opce (Cena podkladového aktiva, Délka života opčního kontraktu a Implied Volatilita). Pro posuzování těchto tří neznámých se pak vžilo označení vyjadřované řeckými písmeny. Míru vlivu změny Ceny podkladového aktiva vyjadřuje hodnota Delta, změnu Délky života opce vyjadřuje Théta a změnu Implied Volatility zachycuje Vega. Tato tři řecká písmena pak zachycují přímou míru vlivu těchto neznámých na cenu opčního kontraktu, jsou to tedy řecká písmena „první kategorie“. Všechna ostatní řecká písmena, se kterými se seznámíte v nějaké literatuře jsou odvozeninami, sloučeninami nebo vyjadřují jiné komplexnější vztahy mezi těmito základními písmeny nebo jejich vztahy k jiným matematickým veličinám spojených nějakou vazbou s cenou opčního kontraktu.
Gamma je nejznámější „odvozené“ řecké písmeno. Jeho hodnota vyjadřuje, jak rychle se mění hodnota Delta vzhledem ke změně ceny podkladového aktiva. Pro jednoduchou představu bych si k hodnotě Delta u každé opce na určitém strike mohl přišroubovat tachometr, vlastně „Gammametr“ a ten by mi ukazoval, jek rychle se bude hodnota Delta měnit v souvislosti se změnou ceny podkladového aktiva. O tom, jak se takový Gammametr vyrábí, jak funguje a jaké pak mohou být jeho hodnoty a co nám naměřené hodnoty říkají, bude dnešní článek.
Matematika Gamma
Pokud přijmu předpoklad, že cenu opcí lze vypočítat pomocí Black-Scholesova oceňovacího modelu, který pracuje s hodnotami šesti faktorů vstupujících do ceny opčního kontraktu (Cena podkladového aktiva, Hodnota strike, Délka života opčního kontraktu, Implied Volatilita, Úroková míra a hodnota případně vyplácené Dividendy za dobu života opce), tak bych měl také pomocí tohoto modelu být schopen vypočítat hodnotu všech základních řeckých písmen a popřípadě jejich odvozenin. V předešlých článcích jsem ukazoval, jak lze takový matematický model „rozklíčovat“ a využít jej k vlastnímu zjišťování hodnoty Call i Put opcí a také jak si například ve vlastním Excelu vytvořit svůj vlastní opční řetězec, v něm pak bylo možné podle jednoho z článků dopočítat také hodnotu Delta takových opcí.
Extrahováním z Black-Scholesova modelu, které můžete v literatuře najít, je hodnota Gamma vypočtena na základě tohoto níže uvedeného vzorce.
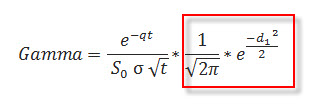 Protože vzorec nevypadá nijak zvlášť pochopitelně, lze si jej pro lepší pochopení „přeložit do češtiny“ a poté bude jeho interpretace možná jednodušší. Záměrně jsem již v tomto vzorci označil červeným obdélníkem pravou část vzorce. Tato pravá část totiž bez nějakého složitého počešťování vyjadřuje Distribuční funkci normálního rozdělení pro hodnotu d1. Tuto hodnotu jsem již zjišťoval a ukazoval její matematický tvar v článku Cena opcí, tam jsem také využíval její hodnotu při určování ceny opce. Její výpočet není složitý a Excel si s ní umí poradit.
Protože vzorec nevypadá nijak zvlášť pochopitelně, lze si jej pro lepší pochopení „přeložit do češtiny“ a poté bude jeho interpretace možná jednodušší. Záměrně jsem již v tomto vzorci označil červeným obdélníkem pravou část vzorce. Tato pravá část totiž bez nějakého složitého počešťování vyjadřuje Distribuční funkci normálního rozdělení pro hodnotu d1. Tuto hodnotu jsem již zjišťoval a ukazoval její matematický tvar v článku Cena opcí, tam jsem také využíval její hodnotu při určování ceny opce. Její výpočet není složitý a Excel si s ní umí poradit.
Co tedy uvidím, dosadím-li si za neznámé výrazy „česká slova“. Na níže uvedeném obrázku je pak vidět česká skladba vzorce výpočtu hodnoty Gamma pro opci na nějakém strike.

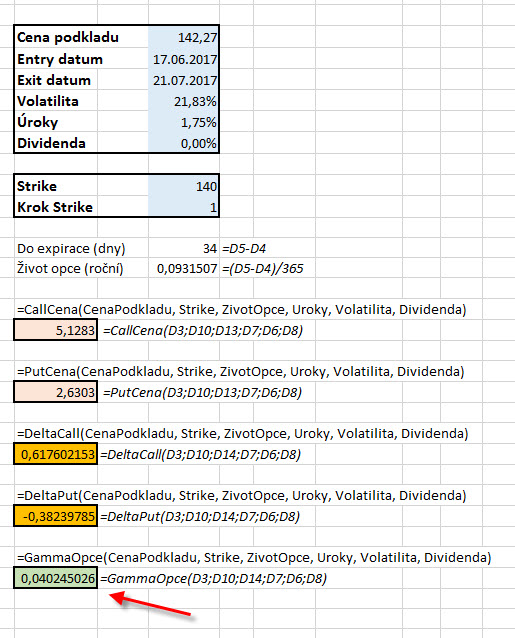
Z českého vzorce zejména vyplývá velmi zjednodušující skutečnost. V čitateli zlomku je exponenciální funkce, jejímž exponentem je součin hodnoty Dividendy a Délka života opce. Protože jsem v článcích výpočtu ceny opcí a v článcích o Dividendách uváděl, že hodnota Dividendy vstupuje do Black-Scholesova vzorce ve svém anualizovaném tvaru, můžeme se na hodnotu exponentu exponenciální funkce dívat, jako by byl téměř nulový a cokoliv téměř na nultou je téměř jedna. Celý výpočet Gamma je pak jednoduchým podílem Distribuční funkce normálního rozdělení a součinu tří „proměnných“ cenotvorných hodnot. Takovou matematickou interpretaci si lze jednoduše převést do Excelu a poté hodnotu Gamma zkoušet modelovat za různých tržních situací. Obrázek z takového Excelu je vidět níže, kdy po změnách parametrů v modrých buňkách můžete pozorovat nejen změnu ceny opcí a jejich Delta, ale také hodnoty Gamma. Funkce Gamma je pak do takového Excelu naprogramována ve VBA a lze ji kdekoliv v tomto Excelu vyvolat v jakékoli buňce jejím vyvoláním „=GammaOpce“. Jednoduchý Excel s touto funkcí je ke stážení zde. Můžete si rovněž prohlédnou její script ve VBA a tento například kopírováním volně přenášet do jiných vlastních sešitů.
Logika Gamma
Matematicky jsem tedy schopen si velikost Gamma spočítat, je to ale k ničemu, když si takové hodnoty nemůžu interpretovat a posuzovat, co mi vlastně říkají.
Gamma tedy vyjadřuje, jak se změní hodnota Delta, když se cena podkladového aktiva zvýší o jeden dolar (nebo bod u futures kontraktů). Toto je jednoduchá interpretace Gamma jako čísla.
Pokud budu mít akcii JPM, která se dnes obchoduje za 86,18 USD, tak Long Call opce na strike 86 bude mít Delta +52 (hodnota Delta Long Call je kladná) a hodnotu Gamma 13. Pokud se cena JPM zvýší o 1 USD na cenu 87,18 USD, potom bude nová hodnota Delta Long Call opce +52 + 13 = 65. Pokud cena JPM klesne 1 USD na hodnotu 85,18 potom bude nová hodnota Long Call Delta +52 – 13 = 39.
Stejný výpočet pak platí pro Put opce. Za stejných podmínek pro akci JPM, která se dnes obchoduje za 86,18 USD, tak Long Put opce na strike 86 bude mít Delta -48 (hodnota Delta Long Put je záporná) a hodnotu Gamma 13. Pokud se cena JPM zvýší o 1 USD na cenu 87,18 USD, potom bude nová hodnota Delta Long Put opce -48 + 13 = 35. Pokud cena JPM klesne 1 USD na hodnotu 85,18 potom bude nová hodnota Long Put Delta -48 – 13 = -61
Gamma lze také interpretovat jako budoucí změnu Delta v procentním vyjádření ke změně ceny podkladové akcie. Toto by mohla být druhá jednoduchá interpretace Gamma jako čísla vyjádřeného jako procento.
Pokud budu mít akcii JPM, která se dnes obchoduje za 86,18 USD, tak Long Call opce na strike 86 bude mít Delta 52 a hodnotu Gamma 13. Gamma si pak mohu vyložit jako procento změny ceny Delta při pohybu akcie JPM. Pokud se cena JPM zvýší o 2 USD na cenu 88,18 USD, potom bude nová hodnota Delta vyšší o 13% pohybu podkladové akcie JPM. 13% ze dvoudolarového pohybu na akcii JPM = 0,26 USD. Nová hodnota Delta pak bude 52 +26 = 78.
Toto je základní náhled na hodnotu Gamma. Protože hodnota Gamma vyjadřuje hodnotu změny Delta, je pak jasné, jaké hodnoty můžu čekat na „Gammametrech“ namontovaných na Delta na jednotlivých strike. Z předcházejícího článku o Delta vyplývá, že Delta opcí hluboce „v penězích“ se blíží k hodnotě 100 a tedy, že pohyb podkladu o jeden dolar bude znamenat zvýšení ceny opce také o stejnou hodnotu, cena opce tak přesně kopíruje hodnotu podkladu. Pokud tedy při ceně JPM 86.18 USD budu mít ITM Long Call opci na strike 70 (závratných 16 bodů „v penězích“), tak tato opce bude mít Delta 100 a hodnotu Gamma 0. Pokud se cena JPM zvýší o +5 USD na cenu 91.18 USD, zůstane Delta mé opce stále 100 a hodnota Gamma bude stále nula. Delta více než 100 být nemůže, protože se opce chová identicky jako podkladová akcie (podklad má vždy hodnotu Delta 100). Protože k hodnotě Delta ve výši 100 již není možné „nic dalšího přidat“, tak hodnota Gamma bude nulová. Hluboce ITM opce mají Gamma zanedbatelnou, hodnota Gamma tak klesá současně s ponořováním „do peněz“ – čím více je opce v penězích, tím má menší Gamma.
Platí to samozřejmě i naopak o velmi vzdálených opcích, které jsou „mimo peníze“. Pokud tedy při ceně JPM 86.18 budu mít OTM Long call opci na strike 110 (značně vzdálených čtrnáct bodů „od peněz“), tak tato opce bude mít Delta nula a hodnotu Gamma nula. Pokud se cena JPM zvýší o 5 USD na cenu 91.18 USD, zůstane Delta mé opce stále nula a hodnota Gamma bude stále nula. Pohyb je velmi malý vzhledem k mému velmi vzdálenému strike a cena opce vůbec nereaguje na pohyb podkladu, je to pro cenu mé OTM opce pohyb tak zanedbatelný, že nemá na cenu pražádný vliv, jako by takový pohyb vůbec nenastal. Velmi vzdálené OTM opce mají Gamma zanedbatelnou, hodnota Gamma pak roste současně s přibližováním strike opce k současné ceně podkladové akcie, čím více se blíží „k penězům“ – tím má větší Gamma.
Z výše uvedeného pozorování hodnoty Gamma na „extrémních“ strike tedy vyplývá, že nejvyšší hodnota Gamma je u opcí, které jsou „na penězích“, tedy na strikes, které jsou nejblíže současné obchodované ceny podkladového aktiva. Gamma pak klesá v obou směrech, jak se vzdaluje od těchto ATM strikes, ať už se strike „ponořuje do peněz“ nebo se od těchto „peněz vzdaluje“.
S touto první poznanou „kvalitou“ Gamma je spojena také její druhá vlastnost, která souvisí se samotnou podstatou Delta. Hodnota Delta u opcí na stejných strike ale v různých expiracích směrem do budoucnosti klesá, klesá tak samozřejmě také hodnota Gamma těchto opcí na těchto stejných strike. Na namontovaných „Gammagrafech“ bych pak směrem do budoucnosti u opcí na stejných strikes viděl jiné – nižší hodnoty. Na níže uvedeném obrázku jsou vidět hodnoty Gamma pro jednotlivé strike opcí akcie JPM, které plasticky zobrazují výše uvedené vlastnosti Gamma.
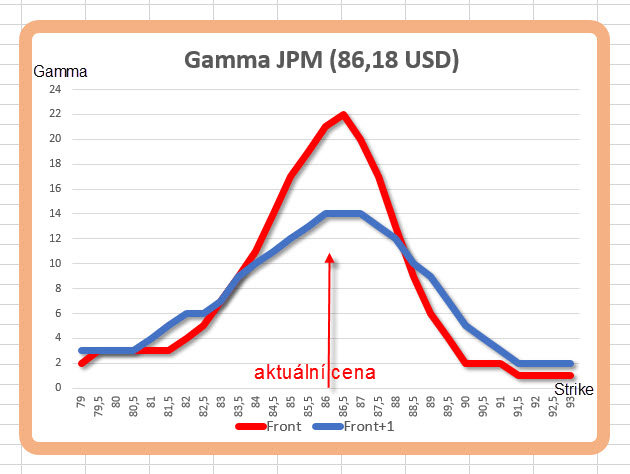
Na obrázku je znázorněná červenou šipkou aktuální hodnota akcie JPM v době tvorby grafu. Červená křivka představuje hodnotu Gamma pro jednotlivé strike opce s nejbližší expirací, modrou křivkou je znázorněná hodnota Gamma pro jednotlivé strike opce se vzdálenější expirací. Je zřetelně vidět nejvyšší hodnoty Gamma na strike co nejblíže současné ceně a také je patrné, že modrá křivka hodnot Gamma opcí se vzdálenější expirací je nižší než křivka hodnot Gamma s bližší expirací.
Stojí za povšimnutí, že Gamma je stejná pro Call i Put opce na stejném strike. Je to způsobeno tím, že absolutní hodnota součtu Delta Call i Put opcí na stejném strike je roven 100. Pokud se podklad pohne nějakým směrem, tak vždy jedna z opcí na své hodnotě přidá a druhá o stejnou hodnotu klesne, Delta jedné z opcí se zvýší, zatímco Delta druhé opce adekvátně klesne, aby pak celkový součet Delta byl stále 100. Tato Call-Put parita nám zajišťuje, že Gamma, která číselně reprezentuje takové zvyšování Delta na jedné opci a klesání Delta na druhé opci musí mít stejnou hodnotu.
Gamma Long opcí je kladná a naopak Gamma Short opcí je záporná.
Pozitivní (kladná) Gamma Long Call znamená, že pohyb podkladového aktiva směrem nahoru zvyšuje kladnou Delta těchto Long Call opcí směrem k hodnotě +100 a pokud cena podkladu klesá, tak se hodnota Delta Long Call snižuje směrem k hodnotě nula. Pozitivní Gamma Long Put opcí způsobuje, že záporná Delta těchto Long Put opcí se snižuje směrem k nule, když cena podkladu roste a naopak pokud cena podkladu padá, tak záporná Delta Long Put opcí je ještě více negativnější až k maximální hodnotě -100.
Negativní (záporná) Gamma Short Call znamená, že pohyb podkladového aktiva směrem nahoru zvyšuje negativitu Delta těchto Short Call opcí směrem k hodnotě -100 a pokud cena podkladu klesá, tak se hodnota Delta Short Call snižuje směrem k hodnotě nula. Negativní Gamma Short Put opcí způsobuje, že kladná Delta těchto Short Put opcí se snižuje směrem k nule, když cena podkladu roste a naopak pokud cena podkladu padá, tak kladná Delta Short Put opcí je ještě více pozitivnější až k maximální hodnotě +100.
Shrnutím těchto významů Gamma můžu pak použít na jednotlivé opční strategie nebo celá opční portfolia. Součtem Gamma všech opčních kontraktů pak mohu dostávat odpověď na otázku, jakému riziku vyplývajícímu z pohybu podkladu je vystaveno například celé mé opční portfolio, jak moc se změní hodnota Delta portfolia, když se změní hodnota podkladu. Obecně pak bude platit, že pokud bude součet Gamma kladný, tak pohyb „je můj přítel“ a naopak, pokud bude Gamma celého portfolia záporná, bude pohyb podkladového aktiva mít nepříznivý vliv na opční portfolio, toto všechno samozřejmě za předpokladu, že by všechny ostatní tržní okolnosti působící na naše portfolio zůstaly konstantní (volatilita a čas). Než ukážu, jak si takovou skutečnost vyhodnocovat pro celé portfolio, shrnu předcházející tvrzení o Gamma na jednotlivých ukázkách.
Na níže uvedeném obrázku je vidět ukázka dvou pozic Long Straddle, pořízených na ATM strike, každá pozice je v jiné expiraci, první má expiraci tento týden (23.7.), druhá pozice příští týden (30.7.).
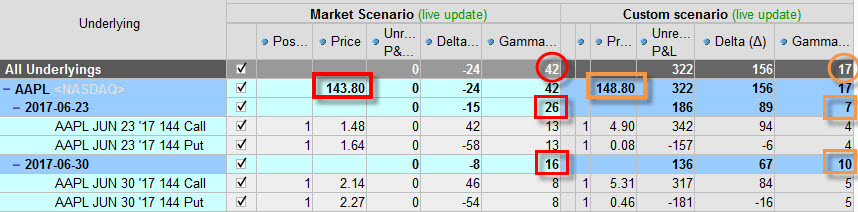
Na obrázku je vidět Gamma pořízené pozice v červených obdélnících za situace, kdy podkladová akcie AAPL se obchoduje za 143.80 USD. Je vidět, že Gamma je kladná, protože jsou pořízeny Long Call a Long Put opce tvořící ATM Long Straddle. Je také patrné, že Gamma je vyšší na bližší expiraci (+26) a nižší na vzdálenější expiraci (+16). Celková Gamma celé opční pozice dvou Long Straddle v různých expiracích je pak +42. Platí tak výše v článku uvedené, že opce na stejných strike, ale ve vzdálenějších expiracích mají Gamma nižší než na bližších expiracích. Na pravé straně obrázku je vidět simulovaná situace, kdy podkladová akcie po uptrendu posílila o +5 USD na cenu 148.80 USD. V hnědých obdélnících je pak vidět hodnota Gamma po takovém uptrendu. Gamma dramaticky poklesla u obou opcí Long Straddle. Je to proto, že obě Long Call obou Long Straddle se dostaly více „do peněz“, kdežto obě Long Put obou Long Straddle se dostaly více „mimo peníze“. Opět tak platí výše v článku uvedené, že nejvyšší Gamma je u opcí, které jsou nejblíže obchodované ceně na ATM strike a jak se opce se svými strike vzdalují od této ceny, tak hodnota Gamma klesá, ať už se jedná o pohyb „více do peněz“ nebo o pohyb „dále od peněz“. Je také patrné, jak je různá Delta po takovém pohybu u opcí s bližší expirací a vzdálenější expirací. Celá pozice je v profitu +322 USD. Nutno také podotknout, že simulace nepočítá s jinými vlivy, jako je změna Implied Volatility (Vega) a působení času (Théta).
Opačnou situaci se zápornou Gamma celého opčního portfolia a simulací pohybu můžu pozorovat na dalším obrázku, jedná se o opačnou pozici k předchozí ukázce, kdy byly pořízeny dvě pozice Short Straddle, pořízených na ATM strike, každá pozice je opět v jiné expiraci, první má expiraci tento týden (23.7.), druhá pozice příští týden (30.7.).
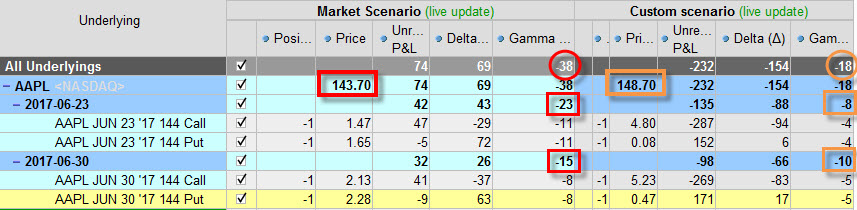
Na obrázku opět vidím Gamma pořízené pozice v červených obdélnících za situace, kdy podkladová akcie AAPL se obchoduje za 143.80 USD. Je vidět, že Gamma je záporná, protože jsou pořízeny Short Call a Short Put opce tvořící ATM Short Straddle. Je také opět patrné, že Gamma je vyšší na bližší expiraci (-23) a nižší na vzdálenější expiraci (-15). Celková Gamma celé opční pozice dvou Long Straddle v různých expiracích je pak -38. Platí tak výše v článku uvedené, že opce na stejných strike, ale ve vzdálenějších expiracích mají Gamma nižší než na bližších expiracích. Na pravé straně obrázku je vidět simulovaná situace, kdy podkladová akcie po uptrendu posílila o +5 USD na cenu 148.80 USD. V hnědých obdélnících je pak vidět hodnota Gamma po takovém uptrendu. Gamma opět dramaticky poklesla u obou opcí Short Straddle. Je to proto, že obě Short Call obou Short Straddle se dostaly více „do peněz“, kdežto obě Short Put obou Short Straddle se dostaly více „mimo peníze“. Opět tak platí výše v článku uvedené, že nejvyšší Gamma je u opcí, které jsou nejblíže obchodované ceně na ATM strike a jak se opce se svými strike vzdalují od této ceny, tak hodnota Gamma klesá, ať už se jedná o pohyb „více do peněz“ nebo o pohyb „dále od peněz“. Celá pozice je ve ztrátě -232 USD. Nutno také opět podotknout, že simulace nepočítá s jinými vlivy, jako je změna Implied Volatility (Vega) a působení času (Théta).
Gamma a Delta-Neutral
Jak takové poznatky využít pro můj vlastní trading nebo alespoň co z nich vlastně ve shrnutí vyplývá? V článku Straddle a Delta-Neutral jsem popisoval, jak zařídit, abych měl portfolio Delta neutrální a vyrobit pro daný okamžik této neutrality nezávislost pozice na pohybu podkladu. Při zapojení poznatků o Gamma se posunu o kousek dál.
Pokud vytvořím portfolio, které je Delta-Neutral, nemohu objektivně vůbec vědět, kterým směrem se vydá podkladové aktivum, zda poroste nebo bude klesat. Co však mohu zjistit je skutečnost, jaký vliv tento následný pohyb bude mít na budoucí hodnotu Delta. Tuto skutečnost mi napovídá Gamma celé komplexní opční pozice.
Gamma pozitivní
Na níže uvedeném obrázku je vidět stejná pozice dvou Long Straddle na ATM opcích ve dvou nejbližších expiracích se simulací, že cena akcie AAPL vzrostla o +5 USD. 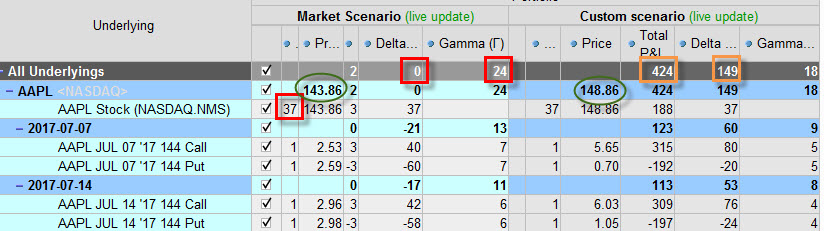
Z obrázku je patrné, že jsem k těmto dvěma Long Straddle pořídil ještě +37 Long akcií AAPL, protože opční pozice vykazovala -37 Delta. Takovou neutralizací jsem dosáhl nulové hodnoty Delta. Gamma mé pořízené Delta-Neutral pozice je kladná (+24). To je velmi důležité zjištění. Pokud cena podkladu – akcie AAPL poroste – poroste také Delta celé pozice. Protože je Delta kladná – bude kladná ještě více, její hodnota poroste, čím větší pohyb tím bude výkonnost vyšší. Protože je Delta kladná a cena podkladu roste, chová se celá pozice jako bych byl „celé portfolio Long“, a to je skvělá konstelace. Mám takové opční portfolio, které při uptrendu má Delta kladnou, takže vydělává. Na pravé straně obrázku je vidět simulace mé Delta-Neutral pozice s kladnou Gamma při uptrendu o +5 USD na akciích AAPL. Delta se vyšplhala z nuly na hodnotu +149 a celkový profit je +424 USD. Protože to je jednoduchá a čitelná pozice, tak vím, že vydělávají obě Long Call a také Long akcie, Long Put opce na hodnotě ztrácejí.
Na dalším obrázku je vidět identickou Delta-Neutral pozici dvou Long Straddle v různých expiracích s pořízenými 37 x Long akciemi, ovšem se simulací, že cena akcie AAPL klesla o -5 USD.
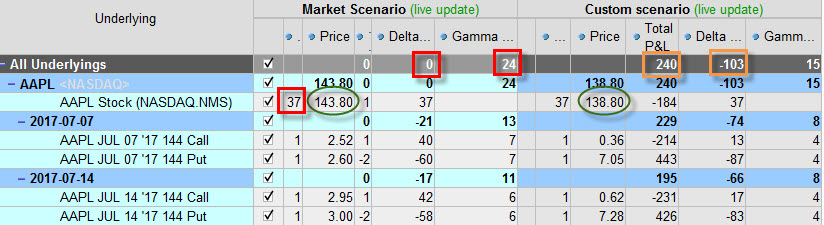
Gamma mé pořízené Delta-Neutral pozice je samozřejmě také opět kladná (+24). Pokud cena podkladu – akcie AAPL bude klesat – bude klesat také Delta celé pozice a bude se propadat do negativního pásma. Protože se stane Delta zápornou – bude se celá pozice chovat, jako bych byl „celá pozice Short“, čím větší propad – tím bude výsledek a výkonnost opčního portfolia lepší, a to také není vůbec špatné. Mám takové opční portfolio, které při downtrendu vydělává. Na pravé straně obrázku je vidět simulace mé Delta-Neutral pozice s kladnou Gamma při downtendu o -5 USD na akciích AAPL. Delta klesla z nuly na hodnotu -103 a celkový profit je +240 USD. Protože to je opět jednoduchá a čitelná pozice, tak vím, že vydělávají obě Long Put, Long akcie a obě Long Call na hodnotě ztrácejí.
Gamma Negativní
Jiný obrázek pak mohu vidět, pokud sestrojím portfolio, které bude sice Delta-Neutral také, ale bude mít ve svém součtu Gamma negativní (zápornou). Takové portfolio je vidět na obrázku, jedná se o pozice dvou Short Straddle na ATM opcích ve dvou nejbližších expiracích. Budu pak simulovat pohyb podkladové akcie směrem nahoru o +5 USD.
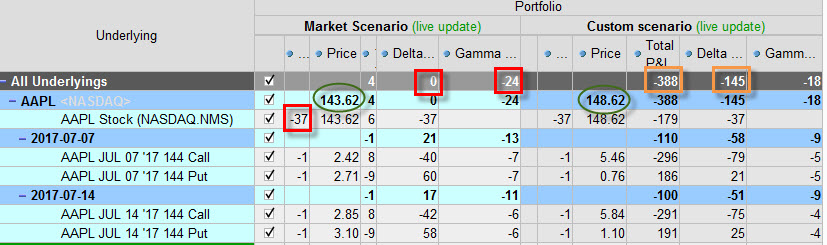
Abych opční pozici s Delta +37 neutralizoval, musel jsem pořídit -37 x Short akcie AAPL. Z levé části obrázku je pak patrné, že Delta je nulová ale Gamma je záporná na hodnotě -24. Pokud cena podkladu poroste, Delta celé pozice bude záporná, čím více poroste, tím více bude negativní. Celé portfolio se díky záporné Delta bude chovat, jako bych byl „celé portfolio Short“, a to při růstu ceny podkladu je přesně to, co nemůžu potřebovat. Na pravé straně obrázku je simulace růstu ceny akcie AAPL o +5 USD, kdy je vidět, že původně nulová Delta je nyní na hodnotě -145 a celková ztráta je -388 USD. Protože to je jednoduchá a čitelná pozice, tak vím, že sice vydělávají obě Short Put, ale prodělávají obě Short Call a také mé Short akcie.
Nejinak tomu bude při pádu podkladové akcie a Delta-Neutral pozicí se zápornou Gamma. Na níže uvedeném obrázku je vidět, jak by to dopadlo v takovém případě, kdy budu simulovat pohyb akcií směrem dolů o -5 USD.
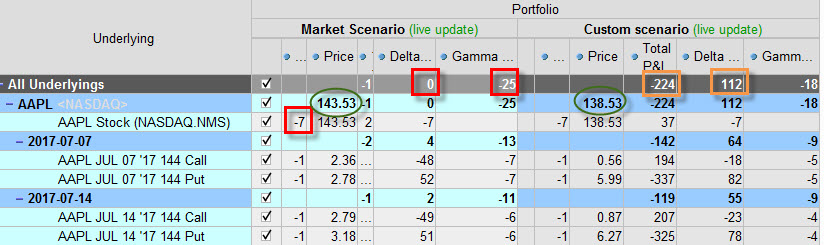
K neutralizaci pozice jsem musel použít -7 x Short akcie AAPL. Delta-Neutral vytvořená pozice na levé straně obrázku má Gamma zápornou na hodnotě -25. Na pravé straně obrázku je opět simulace pohybu ceny akcie – pádu ceny akcie AAPL o –5 USD, kdy je vidět, že Delta se z nuly vyšplhala na +112 a celková ztráta je -224 USD. Záporná Gamma způsobila, že Delta celé pozice se stává pozitivní a roste. Čím více bude cena akcie AAPL klesat, tím více bude Delta „kladnější“. Celá opční pozice se při padajícím ceně AAPL bude chovat jako bych měl pořízeno „celé portfolio Long“, a to je opravdu to, co si nemohu přát. Protože to je opět velmi jednoduchá a čitelná pozice, tak vím, že sice vydělávají obě Short Call a také mých sedm Short akcií, ale prodělávají obě Short Put.
Toto jsou velmi jednoduché příklady, kdy jsem schopen odhadnout, jaké jednotlivé pozice mám (například 2 x Long Straddle). Pokud ale mám složitější multikontraktní pozice, potom mohu vyhodnocením celkové Gamma získat kvalitnější odpověď na jednoduchou otázku, jaká je expozice takového komplexnějšího portfolia vůči pohybům na trhu podkladového aktiva. Nemusím pak být nějaký „vědec“, abych například při pohledu na větší portfolio na obrázku níže mohl ihned posoudit, že jakýkoliv výraznější pohyb takového Delta-Neutral portfolia nebude nic, co bych s nadšením uvítal, protože toto portfolio má velmi zápornou Gamma.
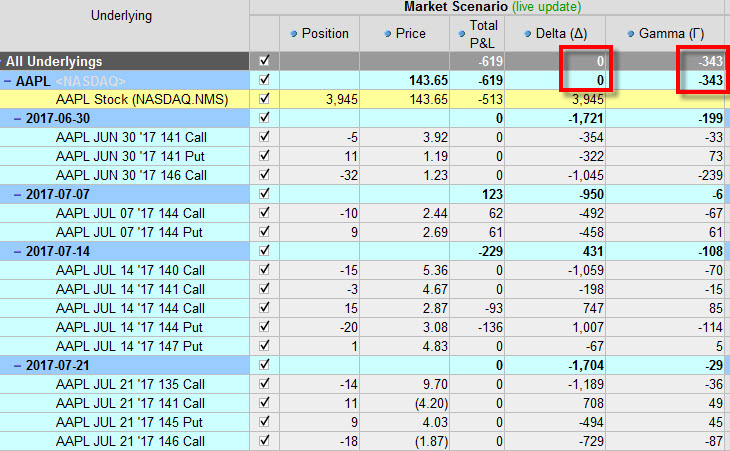
Z výše uvedených příkladů by pak měl vyplynout celkem jednoznačný závěr, že vytvářet pozice nebo portfolia se zápornou Gamma jsou k ničemu a že by pak tedy pouze stačilo být Delta-Neutral s pozitivní Gamma a nemohl bych vlastně vůbec prodělat. Není to pravda. Výše uvedené příklady jsou vytvořené „v izolaci“, kde opční pozice nebyly vystaveny jiným tržním vlivům, zejména vlivu Implied Volatility a běhu času. Pozice, které jsou sice Gamma pozitivní, jako například Long Straddle právě trpí těmito dalšími vlivy, které je nutno při jejich držení eliminovat. Nedostatek pohybu na podkladu, rozpad časové složky ceny opčního kontraktu v závislosti na zkracující se době života opce nebo pokles volatility jsou okolnosti, které takové pozice táhnou do ztrát a je třeba se naučit je eliminovat. Naopak některé jednodušší, typicky Gamma negativní pozice, jako například Iron Condor, Credit Vertical Spread mohou z takových efektů těžit. Nepohyb, pokles Implied Volatility a rozpad časové složky prémia mohou přispět k jejich možné profitabilitě :c)
Sleduj facebook, napiš e-mail nebo tweet
Ahoj Jirko,
co je to prosím Tě za software,který používáš v tomto článku?Předem moc děkuji
Zdraví Jelimán:)
zdravím, je to Risk Navigator, součást platformy TWS od Interactive Brokers. Pokud jsi jejich klient a máš platformu TWS, tak se spouští ze záložky „Analytical Tools“, je to dost intuitivní a můžeš pracovat buď se svým vlastním portfoliem nebo simulovat virtuální pozice nebo celá modelová portfolia, poté je můžeš vystavovat různým tržní situacím, změně ceny, volatility….., ahoj, Jirka