Delta je rozdíl. Delta Praha – Brno je 200 (kilometrů), o tom ale článek nebude. Bude to o Delta opčních kontraktů. Porozumění Delta je jednou ze základních dovedností, kterou by měl disponovat každý opční trader. Toto jednoduché řecké písmeno označuje míru závislosti ceny opce na pohybu podkladového aktiva. Vyjdu ze základní premisy, kterou je tvrzení o velikosti Delta podkladového aktiva. Pokud hledám závislost ceny opce na pohybu podkladu, tak musím vyjít z toho, jak je definována Delta samotného podkladu. Pokud jsou podkladovým aktivem akcie, a pokud opční kontrakt opravdu ve skutečnosti představuje spekulaci se 100 akciemi, tak hodnota Delta jedné akcie je jedna. Pokud cena akcie stoupne o jeden dolar a já mám nakoupenou jednu Long akcii, vydělám +1 USD, pokud mám nakoupeno 100 Long akcií, vydělám +100 USD, Delta 100 Long akcií je +100. Delta Long akcie je pro mě, jako držitele této Long akcie kladná. Pokud budu mít pořízené Short akcie, tak hodnota Delta jedné Short akcie je mínus jedna. Pokud cena AAPL stoupne o jeden dolar a já mám jednu Short akcii AAPL, prodělám -1 USD, pokud mám pořízeno 100 x Short akcií, prodělám -100 USD. Delta Short akcie je pro mě, jako držitele této Short akcie záporná.
Hodnotu Delta opčního kontraktu zobrazuje každá opční platforma, Delta je pak v těchto platformách zobrazována nejběžněji jako desetinné číslo, protože uvádí hodnotu Delta jedné akcie nebo bodu v případě futures kontraktu. Na otázky, kde se ale hodnota Delta vlastně bere, jak se vypočítá a co vlastně znamená bych chtěl odpovědět v tomto článku
Matematika Delta
Delta vychází z Black-Scholesova oceňovacího modelu a za jeho pomoci je také vypočítávána. Pro pořádek uvedu, že tento matematický oceňovací model k výpočtu ceny opčního kontraktu potřebuje znát šest údajů, aby takovou cenu byl schopen stanovit, těmito hodnotami jsou aktuální Cena Podkladu, Strike opce, Délka života opce, Implied Volatilita, Úroky a případná Dividenda vyplácená za života opce. Pokud tedy vychází takový model z těchto hodnot, tak tyto hodnoty také využiji k výpočtu Delta příslušného opčního kontraktu.
Matematická konstrukce výpočtu Delta je základem první a nejběžnější definice či interpretace Delta, se kterou se můžete setkat. Delta nám vyjadřuje, jak se změní hodnota opce, pokud se změní cena podkladového aktiva o jeden dolar (bod). Matematicky lze tuto jednoduchou definici popsat jako derivaci funkce hodnoty opce v závislosti na pohybu podkladového aktiva. O derivaci se tady mluví proto, že derivace vyjadřuje poměr, v jakém růst nějaké proměnné (cena podkladu) odpovídá změně nějaké jiné proměnné (cena opce) pokud platí, že obě proměnné mají nějakou měřitelnou, smysluplnou a vyjádřitelnou funkční závislost. Protože Black-Scholesův model pracuje při výpočtu ceny opčního kontraktu s funkcí Normálního distribučního rozdělení, jejímiž argumenty jsou Cena Podkladu, Strike opce, Délka života opce, Implied Volatilita, Úroky a případná Dividenda vyplácená za života opce, pak hodnotu Delta bude vždy vyjadřovat aktuální hodnota této distribuční funkce s hodnotami těchto argumentů v daný moment, proto matematicky
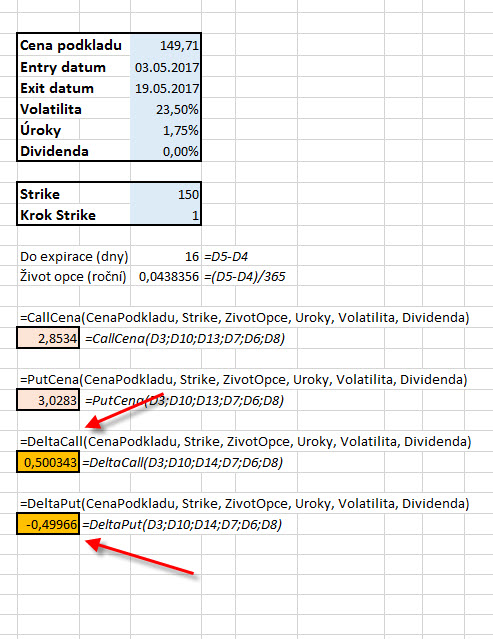
Delta Call = N(d1) a zároveň Delta Put = N(d1)-1
V článku o Cena opce jsem uvedl odkaz na excelovský soubor, který měl naprogramovány funkce výpočtu ceny opcí (CenaCall a CenaPut) podle Black-Scholesova modelu. Protože k vytvoření výpočtu cen opcí podle tohoto modelu bylo také zapotřebí vypočítat hodnotu „d1“, která je součástí matematického vyjádření Delta, nebylo vůbec obtížné si takovou exelovskou funkci pro Delta opcí Call i Put také „zprovoznit“. Tento Excel s těmito vytvořenými funkcemi si můžete stáhnou zde a také si můžete prohlédnout, jaký je jejich jednoduchý script ve VBA. Stačí doplnit šest požadovaných údajů (argumentů distribuční funkce) do modrých buněk a hodnota Delta se Vám objeví kdekoliv, kde v excelovském sešitu vyvoláte funkci DeltaCall nebo DeltaPut a zadáte do nich tyto argumenty z modrých buněk.
Delta a pohyb ceny podkladu
Z matematického pohledu výpočtu Delta Call a Put vyplývá, že Delta pro Call i Put využívají v danou chvíli výpočtu stejné argumenty distribuční funkce Normálního rozdělení, pouze u Delta Put odečítáme vypočtenou hodnotu od hodnoty jedna. Z toho logicky vyplývá, že součet Delta Call a Delta Put by měl být teoreticky vždy v absolutním vyjádření roven hodnotě jedna (nebo 100 pokud opustíme vyjádření v desetinném tvaru). Teoreticky ano, prakticky nikoliv (což je pro tuto chvíli nevýznamné), ale stejně, podívejte se na rozdíly na níže uvedeném obrázku.
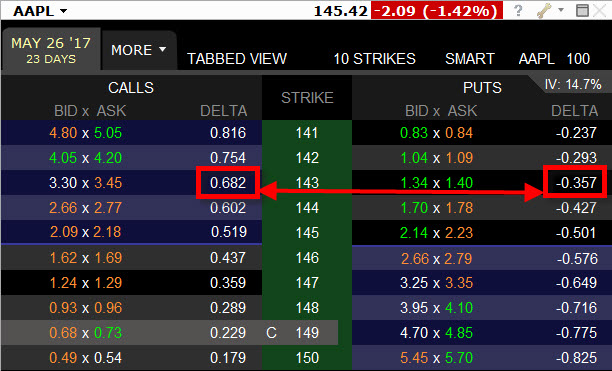
Z obrázku vyplývá, že akcie AAPL má Delta Call opce na strike 143 hodnotu 0,68 a Delta Put opce na strike 143 hodnotu 0,35. Součet není v žádném případě jedna, to ale nevadí pro praktickou interpretaci těchto dvou hodnot. Osobně se mi vyjádření Delta v desetinném tvaru moc nelíbí, protože se nejčastější souvislosti s Delta budou týkat opcí na equities, kde jeden opční kontrakt představuje 100 akcií, budu tedy používat celá čísla, v našem případě tedy Delta Call má hodnotu Delta 68 a Delta Put má hodnotu Delta 35 a samotný podklad má hodnotu Delta rovná se 1 pro každou jednotlivou drženou akcii, tedy 100 pro 100 akcií. Pokud se budeme držet definice Delta o závislosti ceny opce na pohybu podkladu, pak mohu jednoduše konstatovat, že pokud se hodnota podkladu zvýší o jeden dolar (akcie AAPL stoupne ze 145,42 USD na 146,42 USD), pak se ceny opcí na vyobrazeném strike 143 budou chovat následovně:
1/ Pokud budu mít koupenou Long Call 143 opci, tak se cena opce zvýší o hodnotu Delta, tedy o +68 USD. Opce mi vydělá +68 USD. Delta z pohledu držitele Long Call opce je kladná
2/ Pokud budu mít vypsanou Short Call 143 opci, tak se cena opce zvýší o hodnotu Delta, tedy o +68 USD. Na opci prodělám -68 USD. Delta z pohledu vypisovatele Short Call opce je záporná
3/ Pokud budu mít koupenou Long Put 143 opci, tak se cena opce sníží o hodnotu Delta, tedy o -35 USD. Na opci prodělám -35 USD. Delta z pohledu držitele Long Put opce je záporná
4/ Pokud budu mít vypsanou Short Put 143 opci, tak se cena opce sníží o hodnotu Delta, tedy o -35 USD. Opce mi vydělá +35 USD. Delta z pohledu vypisovatele Short Put opce je kladná
5/ Pokud budu mít koupený podklad, například 100 Long akcií, tak se cena mých Long akcií zvýší o hodnotu Delta, tedy o +100 USD. Na akciích vydělám +100 USD. Delta z pohledu držitele Long akcií je kladná.
6/ Pokud budu mít prodaný podklad, například 100 Short akcií, tak se cena mých Short akcií zvýší o hodnotu Delta, tedy o +100 USD. Na akciích prodělám -100 USD. Delta z pohledu držitele Short akcií je záporná.
Takový pohled na Delta z pozice držitele konkrétní opční pozice a pozice podkladu je lehce zapamatovatelný. Je dobré si jej osvojit, pokud ještě nemáte z vlastního obchodování podobné souvislosti mezi Delta a držením konkrétní pozice zažity nebo jste se takovou souvislostí doposud třeba vůbec nezabývali.
Pokud bych se vrátil ke svému článku Conversion + Reversal = Box nebo Time Spread, tak jsem popisoval, že opce Call a Put na stejných strikes vytváří akciové Syntetické Long nebo Syntetické Short pozice, tedy, že takové pozice identicky simulují pohyb podkladů podle toho, jaké opce mám na těchto strikes pořízeny. Pravdivost takových tvrzení mohu doložit například také podle hodnoty Delta takových opčních pozic. Z matematického vyjádření Delta v úvodu článku vyplývá, že součet hodnot Delta Call opcí a Put opcí na stejný strike je roven hodnotě 100 (pokud použiji vyjádření v nedesetinném tvaru). Na obrázku jsou vidět takové syntetické pozice. Short opční pozici představuje červená barva rámečku s hodnotou Delta, Long opční pozici představuje zelená barva rámečku s hodnotou Delta 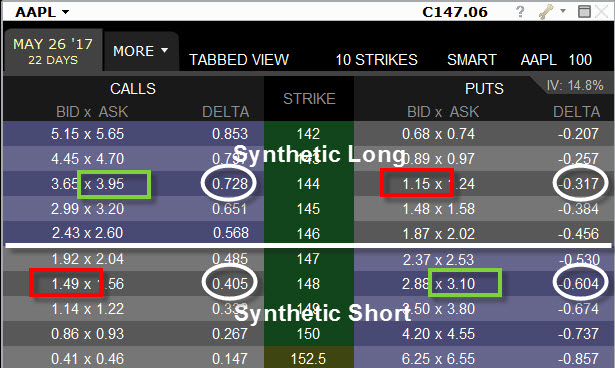
Ve světle pohledu na znaménko hodnoty Delta z pozice držitele různých typů opčních kontraktů podle předchozího odstavce pak mohu konstatovat níže uvedené skutečnosti vyobrazené na uvedeném obrázku.
V opčním řetězci podkladového aktiva akcie AAPL na strike 144 mám pořízenou Long Call 144 a Short Put 144. Z pozice držitele Long Call opce 144 je má Delta ve výši 72 kladná a z pozice držitele Short Put opce je má Delta ve výši 31 také kladná. Celá pozice má tak hodnotu Delta +103, což reprezentuje Delta 100 Long akcií. Součet Delta takových opcí na jakémkoliv stejném strike bude vždycky kladný a bude vždy +100. Mám tedy doopravdy Syntetickou pozici 100 x Long akcie AAPL.
V opčním řetězci podkladového aktiva akcie AAPL na strike 148 mám pořízenou Short Call 148 a Long Put 148. Z pozice držitele Short Call opce 148 je má Delta ve výši 40 záporná a z pozice držitele Long Put opce je má Delta ve výši 60 také záporná. Celá pozice má tak hodnotu Delta -100, což reprezentuje Delta 100 Short akcií. Součet Delta takových opcí na jakémkoliv stejném strike bude vždycky záporný a bude vždy -100. Mám tedy doopravdy Syntetickou pozici 100 x Short akcie AAPL.
Z výše uvedených ukázek by mohla vyplynout také další interpretace Delta. Pomocí Delta můžeme zjišťovat, nakolik nám opční pozice napodobuje pohyb samotného podkladového aktiva. To je také velmi užitečné zjištění. Na obrázku je vidět pět různých opčních pozic na akcie AAPL
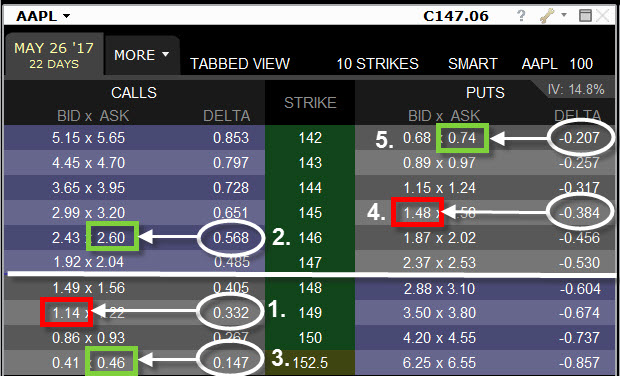
Pozice č.1 je Short Call opce vypsaná OTM na strike 149. Její Delta je 33, jako vypisovatel opce tuto pozici musím vyhodnocovat záporně, má Delta u tohoto opčního kontraktu je -33. Pokud bych opci vypsal za +114 USD, jak je patrné z obrázku, tak při vzestupu ceny podkladové akcie AAPL o jeden dolar by tato opce měla hodnotu 114 USD + 33 USD = 147 USD. Pokud bych chtěl takovou opci jako vypisovatel likvidovat, musel bych vynaložit o +33 USD více a utrpěl bych tak ztrátu -33 USD. Stejnou ztrátu bych ale také utrpěl, kdybych namísto výpisu takové Short Call opce na strike 149 prodal 33 Short akcií AAPL. Těchto 33 Short akcií by vykazovalo stejnou ztrátu -33 USD při vystoupání ceny AAPL právě o jeden dolar. Delta -33 tak znamená, že taková Short Call opce s Delta 33 se chová stejně jako držení 33 x Short akcií AAPL
Pozice č.2 je Long Call opce vypsaná ITM na strike 146. Její Delta je 56, jako držitel opce tuto pozici musím vyhodnocovat kladně, má Delta u tohoto opčního kontraktu je +56. Pokud bych opci koupil za -260 USD, jak je patrné z obrázku, tak při vzestupu ceny podkladové akcie AAPL o jeden dolar by tato opce měla hodnotu 260 USD + 56 USD = 316 USD. Pokud bych chtěl takovou opci jako držitel prodat, utržil bych +316 USD a měl tak profit +56 USD. Stejný profit bych ale také získal, kdybych namísto nákupu takové Long Call opce na strike 146 koupil 56 Long akcií AAPL. Těchto 56 Long akcií by vykazovalo stejný profit +56 USD při vystoupání ceny AAPL právě o jeden dolar. Delta +56 tak znamená, že taková Long Call opce s Delta 56 se chová stejně jako držení 56 x Long akcií AAPL
Takovou interpretací bych si mohl podle Delta vyložit každou opční pozici zvlášť. Pokud bych ale celou interpretaci sumarizoval z pohledu Delta do nějaké tabulky, tak bych mohl při těchto Delta z pohledu jejich hodnot a znamének vyplývajících z pohledu držitele těchto jednotlivých kontraktů zjistit skutečnost, jak je vyobrazena na obrázku
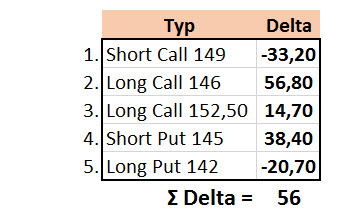
Mohu se dívat na všechny pozice ze všech možných pohledů a hledat například názvy pro jednotlivé kombinace, abych pochopil, co jsem to vlastně „pořídil za zvíře“, ale jedno mám při takovém vyhodnocení jisté. Celá pozice při pohybu ceny akcie AAPL o jeden dolar zvýší svoji hodnotu o +56 USD a chová se úplně stejně, jako bych měl nakoupeno 56 x Long akcií AAPL. Obdobně, pokud cena akcie AAPL klesne o jeden dolar, tak celá opční pozice z obrázku o těchto 56 USD ztratí na své hodnotě, a stejně tolik by ztratilo právě držených 56 x Long akcií AAPL.
Taková výsledná hodnota Delta pak může velmi efektivně podávat traderům minimálně zprávy o tom, jakou skutečnou okamžitou výkonnost má například komplexnější opční portfolio ve vztahu k pohybům cen podkladového aktiva.
Neustálý pohyb podkladového aktiva v čase způsobuje také nepřetržitou změnu hodnoty Delta. Delta se neustále mění právě v důsledku těchto pohybů. Protože ale ve svém výpočtu vychází z Black-Scholesova modelu a ten k těmto výpočtům využívá šest různých vstupních hodnot, tak je patrné, že pokud budu brát za pevné a neměnící se hodnoty vstupující do výpočtu – Strike opce, Úroky a Dividendu, pak na velikost tohoto výpočtu bude mít vliv proměnných Cena podkladu, délka Života opčního kontraktu a aktuální Implied Volatilita. Pokud mám za vysvětlené, že Delta odráží pohyb Ceny podkladu (tuto závislost jsem zachytil v předchozích odstavcích), tak musím prozkoumat, nakolik je dynamika Delta odrazem funkce délky Života opčního kontraktu a Implied Volatility.
Delta a Implied Volatilita
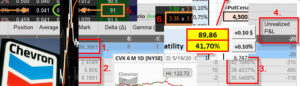
Implied Volatilita velmi podstatně ovlivňuje výši Delta opcí. Pokud je Implied Volatilita malá, tak opce, které jsou „v penězích“ (ITM) mají vyšší Delta než by měly opce, které mají Implied Volatiltu vyšší. Opce, které jsou „mimo peníze“ (OTM) mají u opcí s nízkou Implied Volatilitou nižší Delta než obdobné opce, které by měly Implied Volatilitu vyšší. Podívejte se na obrázek, na kterých jsou vidět opční řetězce akcií CVS (Chevron Corp.) a RL (Ralph Lauren Corp.). Obě stojí stejně (cca 80 USD) a opce mají stejnou expiraci. Horní řetězec akcie zobrazuje cenu opcí CVS s Implied Volatilitou ve výši 15,80% a spodní řetězec akcie RL má Implied Volatilitu 43,90% (více než dvojnásobnou).
Na obrázku jsou vyznačeny ceny stejných opcí na stejných strike. ITM opce klidnějšího a nevolatilního CVS na strike 78 (ITM) mají Delta 75, kdežto u „bouřliváka“ RL je taková Delta jen 62. OTM opce naopak u klidného CVS na strike 81 má Delta jen 31, kdežto u velmi volatilního RL je tato Delta vyšší a má hodnotu 45.
Nabízí se tak další z interpretací Delta. Delta nám sděluje, jaká je pravděpodobnost, že opce bude při expiraci v penězích. Pravděpodobnost, že opce na ITM strike 78 skončí v penězích je tak u titulu CVS 74%, kdežto u titulu RL jen 62%. Stejně tak u OTM opcí. Pravděpodobnost, že opce na OTM strike 81 skončí v penězích je u titulu CVS 31%, kdežto u titulu RL je 45%. Má to logiku. Volatilnější titul vykazuje vyšší pravděpodobnost možného budoucího pohybu a také vyšší pravděpodobnost, že bude opce nakonec někde jinde než je nyní. Klidnější akcie zůstanou klidnější a pokud je dnes sledovaný strike například „mimo peníze“ tak s větší pravděpodobností „mimo peníze“ také zůstane. U volatilnějších titulů je naopak úvaha opačná.
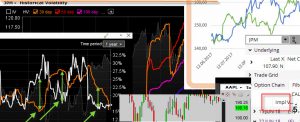
Delta a čas
Plynutí času – délka života opčního kontraktu – také ovlivňuje výši Delta tohoto příslušného opčního kontraktu. Opce s kratší dobou do expirace mají Delta ITM opcí vyšší než je Delta na stejných ITM strikes u opčních kontraktů se vzdálenější expirací. Pro Delta u opcí se strike OTM pak platí pravý opak. OTM opce s bližší expirací mají takovou Delta nižší než opce se stejným strike se vzdálenější expirací. Na obrázku je vidět opět dva opční řetězce akcie AAPL, kde jsou vyobrazeny jednotlivé Delta. Opce mají stejnou cenu (obě jsou to akcie AAPL) a téměř identickou Implied Volatilitu, liší se pouze dobou do expirace. Na prvním horním obrázku jsou opce s expirací za 8 dnů a na spodním jsou s expiraci za 15 dnů.
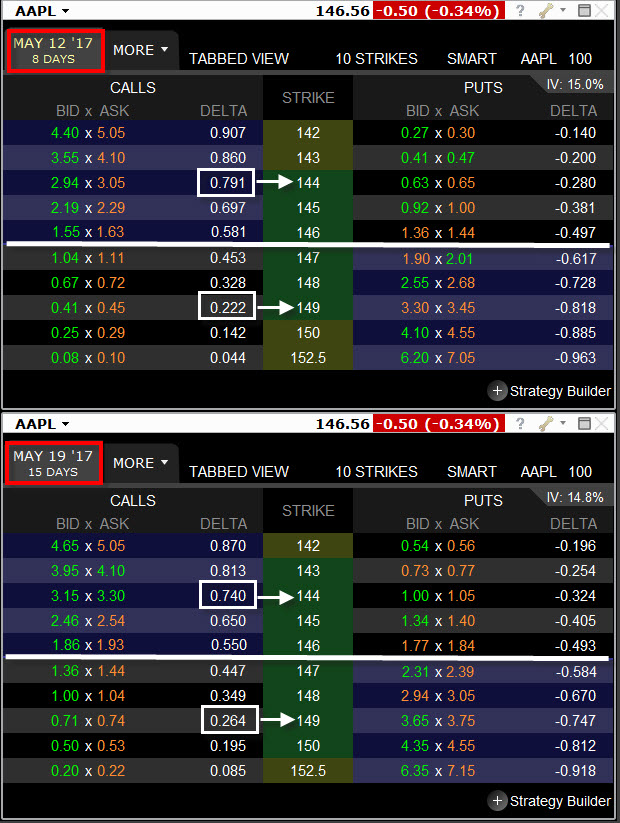
Opce s bližší expirací mají na ITM strike 144 Delta 79, kdežto na stejném strike se vzdálenější expirací je taková Delta na tomto strike jenom 74. Naopak OTM strike 149 u opce s bližší expirací má Delta pouze 22, kdežto Delta na stejném OTM strike 149 má Delta vyšší, a to na hodnotě 26.
Dynamika Delta má přímý vliv na naše opční portfolio. Určuje jeho momentální potenciál a také, a jak se tento potenciál mění v čase, a to jak působením pohybu podkladu, změnou času doby života opce směrem k její expiraci a také změnou Implied Volatility. Všechny tyto faktory působí na držené opční kontrakty současně. Porozumět takovým efektům určitě není na škodu a může poskytovat větší nadhled na stavbu, držení a řízení portfolia :c)
Sleduj facebook, napiš e-mail nebo tweet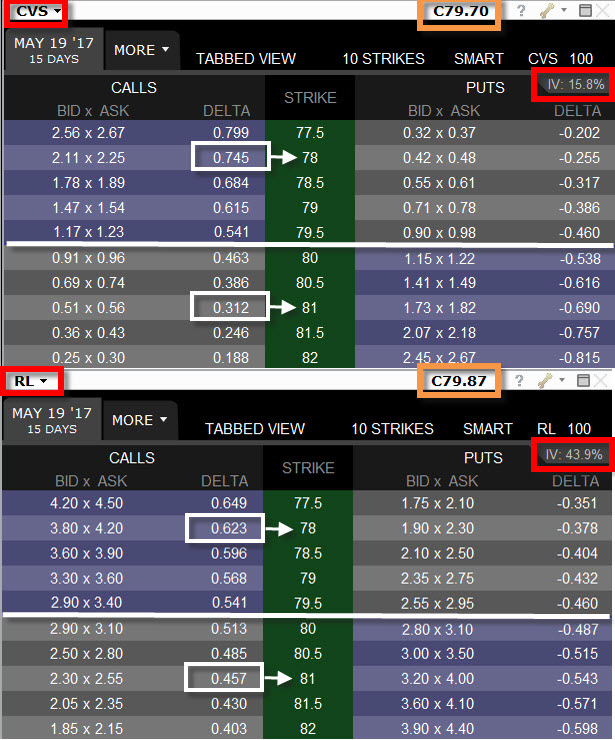
Ahoj, myslim si, ze jsem v clanku nasel chybu. U synteticke short pozice pises, ze „V opčním řetězci podkladového aktiva akcie AAPL na strike 148 mám pořízenou Short Call 148 a Long Call 148“ – Pokud synteticka long obsahuje Long Call a Short Put, nemela by pak short pozice mit Short Call a Long Put misto Long Call?
Kdyztak me prosim oprav, kdybych se mylil.
H.
Ahoj Honzo, no jasně, je to písařská chyba, chybně jsem to z obrázku přenesl do textu, díky za pozorné čtení a upozornění na chybu, Ahoj Jirka :c)
Ahoj Jirko, díky za další super článek. Kolikrát už jsem o deltě četl, na různých webech a po čase hledal znovu a říkal si, vždyť už jsem o tom četl… Teď už mám jasno, resp. už nemusím hledat, kdyžtak pro oživení vím kam kouknout 😉
Milan
Ahoj,
mohl bys mi prosím objasnit naprosté zmatení ohledně Delta a IV. Už se z toho doma stavím na hlavu 🙂
V poznámkách z minulého kurzu mám napsáno, že zhruba delta 0,16 se rovná 1.směrodatné odchylce. A trh se udrží v pásmu +- 1 směrodatná odchylka na 68 %.
Ty v článku ale píšeš „Delta nám sděluje, jaká je pravděpodobnost, že opce bude při expiraci v penězích“
Znamená to tedy, že opce s deltou 0,16 má pravděpodobnost 16 % že bude v den expirace v ITM ? Nebo těch 32 % ( 1-68).
Díky moc.
Až na tohle moje zmatení opět skvělej článek !
Ahoj,
Hodnotu Delta na úrovni 16 mohu interpretovat jako 16% pravděpodobnost, že opce skončí ITM při expiraci a tato domněnka vychází z Black-Scholesova oceňovacího modelu, je to ale velice jednoduchý a nepřesný způsob, jak si Delta vyložit. Vysvětlit návaznost takové interpretace na BS oceňovací model je ale sofistikovanější záležitost a značně by překročila rámec tohoto komentáře.
To, že se cena nějakého investičního nástroje bude pohybovat v pásmu +/- první standardní odchylky je založeno na předpokladu, že cenové pohyby jsou náhodné a jejich (například mezidenní) pohyb má Normální rozdělení, pak mohu pohybu v tomto pásmu přiřadit pravděpodobnost cca 68%. Křivka hustoty pravděpodobnosti Normálního rozdělení má tvar Gaussovy křivky a je symetrická podle střední hodnoty (meanu) a bude to znamenat, že se hodnota mezidenního pohybu bude nacházet v pásmu -34% pod střední hodnotou nebo +34% nad střední hodnotou (dohromady 68%)
Mohu se tedy podívat, jaký strike reprezentuje Delta 16 a jak je vzdálen od současné ceny, která by mohla být brána jako střední hodnota. Tuto vzdálenost strike s Delta 16 od střední hodnoty pak můžeš podrobit zkoumání, jestli je ve vzdálenosti, která tvoří hranici vytyčenou první standardní odchylkou…oba způsoby pravděpodobnosti a jejich vztah jsem popisoval v tomto článku https://dobretrejdy.com/?p=2654 na praktické ukázce …:c)
Díky moc. Nastudoval jsem si uvedený článek a už je mi to jasnější.
Ještě pro ověření 🙂 Dá se tedy říct, že pravděpodobnost přes deltu je vypočítána přes BS model, tedy přes Inmplikovanou volatilitu, zatímco pravděpodobnost přes směrodatnou odchylku je vypočítána na základě minulých pohybů, teda spíše přes historickou volatilitu?
Ahoj,
hodnota Delta je jedním z výstupů BS modelu (stejně jako zbylá řecká písmena) a všechny vstupní údaje, které do BS oceňovacího modelu vstupují, mají na Delta vliv. Implied Volatilita, jako jedna z klíčových položek výpočtu, má na Delta samozřejmě velký vliv. Pokud bych si opět představil Gaussovu křivku pro Normální rozdělení, tak Implied Volatilita má na její tvar podstatný vliv – pokud bude IV nízká, tak křivka bude úzká a hodně špičatá a bude tom znamenat, že většina hodnot se bude nacházet v nedaleké vzdálenosti od střední hodnoty, pokud bude IV vysoká – budou se hodnoty rozprostírat ve větších vzdálenostech od meanu, její tvar tedy bude plošší a bude více rozplizlý do obou stran. Z takového „grafického pohledu“ je pak jasné, že pravděpodobnost pohybu v rozsahu jedné směrodatné odchylky bude u ploššího průběhu křivky (vyšší IV) ve větší vzdálenosti od střední hodnoty (aktuální ceny) než u špičaté křivky (nižší IV). Proto také Delta u opčních strike, které jsou stejně vzdálené od aktuální ceny (OTM), bude nižší u titulů, které mají nižší Implied Volatilitu než u titulů, které mají vyšší Implied Volatilitu.
Pokud znám Implied Volatilitu (vidím ji například v opční platformě), tak tato je interpretována jako roční pravděpodobnost pohybu s pravděpodobností 68%, tedy první standardní odchylky. Toto číslo si mohu převádět na jakýkoliv jiný časový úsek, než je tento jeden rok (https://dobretrejdy.com/?p=2109) a z něj usuzovat, jak trh nahlíží na možnost pohybu s touto pravděpodobností v tomto časovém období. Základním předpokladem ale je, že cena se pohybuje náhodně, tyto pohyby mají normální rozdělení a zcela zásadní pak je, co číslo (IV%) z platformy znamená, jak se k němu její autoři dopátrali a jestli je vůbec správné (momentálně tyto úvahy formuluji do nového článku). Není tak obtížné matematicky velmi rychle zjistit, jak se aktuálně pozorovaná IV promítá do pravděpodobnosti pohybu v nějakém cenovém pásmu (+/- 2 SD, +/- 15 USD….atd.). Pokud za hodnotu IV dosadím hodnotu Historické Volatility (té co skutečně nakonec byla), tak mohu usuzovat, jak se tyto pohyby nakonec udály, jestli IV byla správně určena a jestli se tedy pravděpodobnosti naplnily. Toto pak může vést ke srovnání, jestli je aktuální cena opce vysoká nebo nízká. Stačí jen letmý pohled na grafy HV a IV a je jasné, že existují výrazné rozdíly, nesmím zapomenout, že také HV mohu vypočítávat mnoha způsoby (https://dobretrejdy.com/?p=267)….:c)