Kupuji dluhopis. První věta z minulého článku se tak opakuje, a protože jsem si v tomto předcházejícím článku udělal svou analýzu základních vlastností dluhopisu, nyní je mé rozhodování již zaměřeno na vlastní výkon zamýšlené investice. Jak změřit investici do cenného papíru s pevným výnosem je opravdu výzva a z nabízeného řešení pak vyplyne, proč jsem seriál o dluhopisech začal dvěma veskrze nudnými články s úvahami o současné a budoucí hodnotě peněz :c)

   Nákup dluhopisu pro mě představuje investici, od které samozřejmě čekám zhodnocení s přiměřeným rizikem. Od vložené částky do nákupu dluhopisu mohu očekávat dvě základní verze chování spojené s jedním (opět základním) předpokladem, které budou definovat můj celkový výnos, toto vše se pak odvíjí od dvou základních typů dluhového cenného papíru, kterými se nyní budu zabývat. Dluhopis pořídím za nějakou pořizovací cenu (Present Value) a u splatnosti (Maturity) obdržím jeho nominální hodnotu (Face Value), do splatnosti dluhopisu kasíruji vyznačené kupóny vyjádřené procentní sazbou p.a. z Face Value, to je verze představující první možnost, tedy pořízení klasického dluhopisu s kupónem. V druhé možnosti vývoje celkového výnosu z držby dluhového cenného papíru pořídím dluhopis za nějakou pořizovací cenu (Present Value) a u splatnosti (Maturity) obdržím jeho nominální hodnotu (Face Value), tyto dluhopisy jsou ale bez kupónu (tzv. „zero-coupon bonds“, „zerobonds“ či „zeroes“). Vyslovený základní předpoklad spočívá v představě, že kupóny, které obdržím při investici do dluhopisu (první verze) neutratím, ale reinvestuji a součástí celkového výnosu je pak výnos také z takto reinvestovaných kupónů, zerobondy (druhá verze) tento předpoklad postrádají, protože žádné kupóny k reinvestování nenabízejí. Ostatní typy dluhopisů, například s plovoucím (variabilním) kupónem, inflační dluhopisy apod. pak při měření výnosů budou vycházet z podobných předpokladů, výpočty budou ale těmto odlišnostem patřičně a vhodně přizpůsobeny.

   Předpoklad, vyslovený v předchozím odstavci, tedy reinvestice kupónů za dobu držení dluhopisu, nemusí být naplněn, například z rozhodnutí, že tyto nashromážděné kupóny využiji pro jinou investici nebo je prostě utratím, nebudu tak počítat s jejich reinvesticí za aktuální úrokovou sazbu. Díky absenci tohoto průběžného výnosu mohu na změření výnosu aplikovat jednoduchý početní postup.

Current Yield (Aktuální výnos)

   Absence reinvestování přijatých kupónů zjednoduší pohled na měření výnosu dluhopisu do jednoduchého vzorce.

   Poměr „kolik mi to vynese ročně“ a „kolik na to musím vynaložit“ není zapotřebí nějak významně komentovat. Poměřím kupónový výnos s nabízenou cenou za dluhopis. Mohu pak zcela konkrétně zjistit výnos dluhopisu od společnosti MSFT podle obrázku níže:

   Aktuálně mohu pořídit tento dluhopis za cenu (Ask) 942.00 USD a roční kupónový výnos (Coupon) představuje 2.40% p.a., konkrétně 24 USD ročně.

   Current Yield představuje částku 2,547% p.a. Mohu se spolehnout (jedná se „tříáčkový“ dluhopis), že tento výnos budu schopen přijímat na svůj účet za dobu jeho života vzhledem k jeho pořizovací ceně. Je patrné, že takto změřený výnos trpí základní vadou, tedy nezohledňuje kapitálový výnos/ztrátu z dluhopisové investice. Z obrázku pozoruji, že Face Value dluhopisu je 1000 USD a já jej mohu pořídit za 942.00 USD. Při držení dluhopisu do maturity přidám k výnosu také profit z rozdílu mezi pořizovací cenou dluhopisu a jeho Face Value, tento jsem totiž pořídil za diskont, tedy za méně než je Face Value. V mém konkrétním případě bych u maturity při vypořádání inkasoval navíc (-942.00 USD +1000.00 USD) částku +58.00 USD za každý držený dluhopis. Pokud bych naopak dluhopis pořídil „s prémiem“, tedy za cenu vyšší, než je Face Value, tak vypočítaný Current Yield nezohledňuje ztrátu kapitálu, kterou představuje opět rozdíl mezi pořizovací cenou a Face Value, takovou situaci mohu pozorovat například na obrázku níže:

   Dluhopis společnosti Ford nabízí kupón 66,25 USD ročně a aktuálně se nabízí za 1030.23 USD, potom:

   Current Yield bude sice činit 6.43% p.a., při jeho splatnosti ale zcela jistě utrpím ztrátu -30.23 USD na každém drženém kusu, to je totiž rozdíl mezi jeho pořizovací cenou (-1030.23 USD) a Face Value (+1000.00 USD). Přestože výpočet Aktuálního výnosu trpí vadou nezohlednění kapitálového výnosu/ztráty z držení dluhového cenného papíru, může být alespoň prvotním základním vodítkem, jak se k vyhodnocení ve smyslu „cena/výkon“ postavit.

   Kupuji dluhopis jako investici a takto s ní budu chtít také pracovat. Bude mě tak zajímat, jak mohu využít všech peněžních toků, které z pořízení dluhopisu vyplývají. Měření výnosu by pak mělo tyto všechny budoucí peněžní toky zahrnovat a výsledkem měření by pak mělo být nějaké roční procentní ohodnocení vložené investice. Přestože tedy pomýšlím na nejnovější model Ferrari, budu chtít se svou dluhopisovou investicí naložit opravdu zodpovědně a využít vše co nabízí.

   Výchozím předpokladem výpočtu zjištění ceny dluhopisu budou teoretické skutečnosti popsané v článku Dluhopisy – II.. Zjistit, jaký budu z nakoupeného dluhopisu mít výnos, mi umožní posouzení jeho vlastností, které mohu z jeho popisu odvodit. Pohledem do obchodní platformy zjišťuji, jaká je jeho aktuální cena, jaká je jeho Face Value, jaký je kupónový výnos a jaká je frekvence jeho výplaty, kdy je termín nejbližší kupónové výplaty a kdy je datum jeho poslední výplaty se splatností Face Value. Aktuální cena dluhopisu, kterou vidím ve své platformě, je vyjádřením přání prodejce dluhopisu, který do něj promítnul očekávání a stav dluhopisových trhů v kombinaci s rizikem, které držení daného dluhopisu přináší spojené s očekávaným výnosem tohoto cenného papíru do jeho splatnosti. Nemám ponětí o motivech prodejce a nechci se nyní zabývat rizikem z držení dluhopisu (o tomto v dalším článku), bude mě nyní pouze zajímat, jaký výnos do splatnosti dluhopisu mohu očekávat a jak jej mohu stanovit.

   Všechny poznané platby, které mě v souvislosti s dluhopisem čekají v budoucnosti, mohu jejich diskontováním k dnešnímu dni vtělit do aktuální ceny dluhopisu. Základním vzorcem pro zjištění současné ceny cenného papíru s pevným výnosem je modifikovaný a upravený vzorec z článku Dluhopisy – II. a mohl by vypadat takto: 

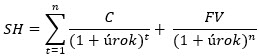
   Není třeba se takového chuchvalce obávat. Vyjadřuje vše, co mohu od dluhopisu čekat. SH je současná hodnota dluhopisu, C je kupónová výplata za vyznačenou periodu, FV je Face Value – částka nominálu splatná k Maturity Date (dni splatnosti) a úrok je sazba, kterou diskontuji všechny budoucí platby k dnešnímu dni. Každou kupónovou výplatu (jednu až do hodnoty n – podle toho, kolik jich je) diskontuji k dnešnímu dni (zjišťuji, jejich aktuální hodnotu) a nakonec diskontuji Face Value k dnešnímu dni, abych součtem těchto diskontovaných hodnot zjistil současnou cenu dluhopisu. V modelovém případě dluhopisu se splatností za čtyři roky s Face Value 1000 USD, ročním kupónem 50 USD a při úrokové sazbě 4% p.a., mohu zjistit současnou hodnotu tohoto dluhopisu takto:

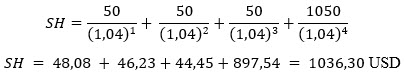
   Z výpočtu mohu vypozorovat, že tento dluhopis by měl mít za zadaných výpočetních podmínek současnou hodnotu 1036.30 USD. Tento vzorec a postup výpočtu pak budiž základním stavebním kamenem další úvahy o měření výkonu dluhopisů 

Yield To Maturity (Výnos do splatnosti)

   Výnos do splatnosti (Yield To Maturity – YTM) je považován za nejběžnější měřítko výnosu dluhopisu. Je vyjádřen procentní sazbou za rok (% p.a.) a ukazuje s jakou mírou výnosnosti mohu u dluhopisu počítat. Jak se k ní dobrat je základní premisou k pochopení její interpretace a spolehlivosti. V předchozím odstavci jsem popsal základní teoretický vzorec výpočtu současné ceny dluhopisu při zjištěných předpokladech – velikosti kupónu, frekvenci kupónů, době do splatnosti a úrokové sazbě, z těchto poznaných údajů pak vypočítám současnou cenu dluhopisu. K čemu mi to ale je, když současnou cenu dluhopisu znám? Mohu se na ni podívat do obchodní platformy a nemusím ji složitě počítat! Proto si musím položit jinou otázku. Kde se vzala ta úroková sazba v mém výpočtu, která mi „to celé“ diskontuje na současnou cenu? To je ta správná otázka, ptám se totiž na úrokovou sazbu, která mi ze všech možných plateb, které diskontuji, vytváří současnou cenu dluhopisu, na kterou se dívám. Tato poptávaná a hledaná úroková sazba, která mi „nadiskontuje“ budoucí platby do současných hodnot tvořících aktuální cenu dluhopisu je právě výnos do splatnosti, tedy Yield To Maturity (YTM).

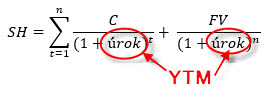
   Pokud budu chtít dostat z výše uvedeného vzorce hodnotu úroku (YTM) pomocí všech ostatních poznaných hodnot, čeká mě nelehký úkol spojený s iterací, popsaný v článku Dluhopisy – II., který však velmi jednoduše zvládnu pomocí Exelu. Přestože mi Excel poskytuje velmi dobrý a elegantní nástroj na výpočet tohoto YTM, hledám totiž Vnitřní Výnosové Procento (funkce =IRR) série budoucích cash flow, musím své hledání YTM konfrontovat s existencí různých typů dluhopisů, vytvořit pro pochopení YTM správné předpoklady, a nakonec zohlednit při výpočtu různé technické detaily.

     Zerobonds

   Pořídit dluhopis bez kupónu není nic neobvyklého. Naopak, jedná se o velmi běžnou investici například do Treasury Bills, které nemají žádný kupón, ale prodávají se s diskontem k Face Value. Neexistence kupónu pak přináší značné zjednodušení výpočtu YTM.  

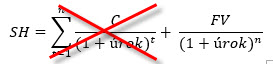
   Z celého vzorce pro výpočet současné hodnoty SH zerobondu totiž odpadá velmi pracná pasáž s diskontováním kupónových plateb a zůstane pouze část, která vyjadřuje diskontování Face Value. Bezkupónové dluhopisy totiž žádný kupón nenabízí, není tak co diskontovat :c). Nákupem zerobondu mě čeká pouze jediné budoucí cash flow a tím je jeho budoucí prodej nebo vypořádání ve výši Face Value při splatnosti, v mém případě druhá možnost, protože hledám výnos „do splatnosti“ dluhopisu. Potom, při vyloučení části vzorce označené červeným křížkem reprezentující diskontování průběžných kupónů, mohu pozorovat:

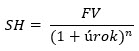
    Hledání výnosu do splatnosti se tak velmi příjemně smrsklo do jednoduché algebry, kde budu chtít vyhledat hodnotu úrok z výše uvedeného vzorce, bude to hodnota takové úrokové sazby, která způsobuje, že budoucí Face Value má současnou hodnotu SH:

   Po příslušných úpravách, mohu vypozorovat, že se mi podařilo „vyseparovat“ hodnotu úrok do velmi dobrého formátu pro stanovení výnosu do splatnosti (YTM) jakéhokoliv zerobondu takto:

   Nákup zerobondu se splatností za čtyři roky s Face Value 1000 USD a aktuální cenou 880 USD, by pak přineslo tento výsledek při vyhledání YTM:

   Tímto jednoduchým výpočtem bych pak mohl zjistit, že takto nabízený zerobond by poskytoval výnos 3.24 % p.a. Za jakých podmínek? Zerobond poskytuje tento výnos za jediné podmínky, tedy musí být držen do splatnosti, kdy obdržím při vypořádání Face Value ve výši 1000 USD, tento úrokový výnos mi tak již nikdo při splnění této podmínky nevezme. Odpadá tak vliv pohybu jeho ceny, pokud bych se rozhodl tento dluhopis prodat před jeho splatností a nemusím se zabývat otázkou reinvestování kupónů, jako u klasického kupónového dluhopisu.  

   V praktické ukázce a s potřebou více výpočet výnos ze zerobondu plastičtěji přiblížit, je na obrázku níže patrné, že jsem 29.12.2022 nakoupil na obchodní účet 50 ks zerobondů – Treasury Bills APR25 2023.

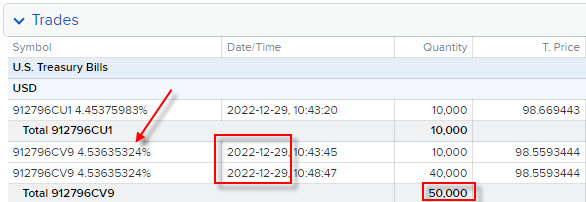
   Jednalo se o dluhopisy se splatností 25.4.2023 a za tyto dluhopisy jsem po započtení komisí zaplatil 98,5793% jejich Face Value, tedy nakoupil jsem jeden kus za 985.793 USD, tato cena je zobrazena na obrázku z obchodní platformy TWS níže červenou šipkou:  

  Protože se jedná o dluhopisové cenné papíry držené kratší dobu než jeden rok, musím provést mírnou úpravu vzorce pro výpočet YTM tak, aby vyjadřovala právě takovou dobu do splatnosti kratší než kalendářní rok. V článku Dluhopisy – I. jsem popisoval, jak mohu vypočítat hodnotu peněz pro období kratší nebo delší než jeden rok, budu aplikovat tento postup také na své zerobondy. Nákup zerobondů 29.12.2022 se splatností 25.4.2023 určuje dobu do splatnosti těchto zerobondů ve výši 117 kalendářních dnů. Mohu pak na výpočet YTM těchto dubnových zerobondů aplikovat vzorec:  

   Pořízením těchto zerobondů mě výnos do splatnosti (YTM) ve výši 4.565 % p.a. nemine. Mohu tak porovnat tuto hodnotu s obrázkem z výpisu účtu výše, kde červenou šipkou je odhadovaná výše YTM u tohoto zerobondu také vyznačena podle výpočtu mého brokera.

   Mohu toto vše samozřejmě svěřit excelovskému sešitu, kde budu mít celý výpočet okamžitě k dispozici. Na níže uvedeném obrázku je v ukázce excelovského sešitu popsán způsob výpočtu YTM nakoupeného zerobondu společně s možností modelovat výnos do jakékoliv požadované pořizovací ceny.

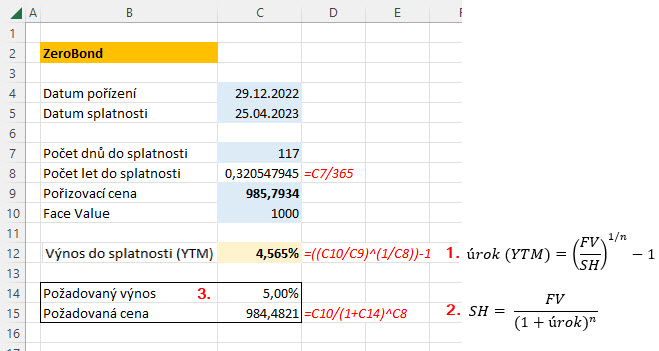
   Výpočet YTM zerobondu (1) je prostým převedením vzorce popsaného výše do excelovského vzorce. Mohu ale také, za použití původního vzorce pro hledání požadované současné hodnoty dluhopisu podle zadaného úrokového výnosu (2), modelovat situaci, kdy budu chtít nakoupit za určitou cenu, která bude charakterizovat požadovaný výnos. Pokud bych tedy chtěl po nakupovaném zerobondu dne 29.12.2022 se splatností 25.4.2023, aby mi přinesl vyšší výnos například 5% p.a. (3), musela by být jeho pořizovací hodnota nižší, tedy na úrovni nejvýše 984,4821 USD. Změnou požadované úrokové sazby pak mohu tento úrok měnit a pozorovat, jak se promítá do požadované ceny nakupovaného zerobondu.

   Dluhopisy s kupónem

   Stanovit výnos dluhopisu vyplácejícího kupón v pravidelných intervalech je úkol, který by měl řešit již vzpomínaný vzorec pro výpočet současné hodnoty cenného dluhového papíru diskontováním budoucích peněžních toků.

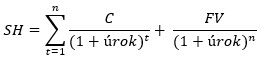
   Už bylo naznačeno, že proměnná úrok je hledaný YTM a že výpočet není jednoduchý, pokud bych chtěl použít tužku a papír, nicméně pomocí Excelu toto problém není. V „rozložené“ formě tohoto vzorce je pak patrné, že pro stanovení YTM bude stačit znát pořizovací cenu dluhopisu, Face Value, výši vypláceného kupónu a jeho periodu, a nakonec počet period do splatnosti dluhopisu. Potom, za předpokladu použití vhodného výpočetního nástroje, budu moci stanovit YTM pozorovaného dluhopisu. Na obrázku níže je opět zobrazen dluhopis společnosti Ford se základními údaji:

   Pokud bych nyní tento dluhopis nakoupil za 1042.50 USD, tak mohu inkasovat kupón ve výši 6.625% p.a. v pravidelných půlročních intervalech ve výši +33,125 USD až do jeho splatnosti, tedy do 15.2.2028. Protože do splatnosti dluhopisu ode dnešního dne je pět let, čeká mě deset výplat kupónů – počet period je tak 10. Toto mi postačí ke zběžnému výpočtu výnosu do splatnosti pomocí excelu.   

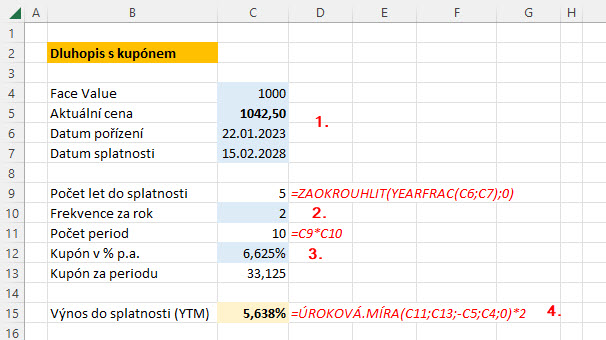
   V excelovské tabulce vyplním modré buňky, vše ostatní obstarají výpočty. Zadání Face Value, aktuální ceny, data pořízení a data splatnosti dluhopisu netřeba významně komentovat (1.). Datum pořízení a datum splatnosti mi vygeneruje počet let do splatnosti dluhopisu (hodnota 5 let). Protože se jedná o dluhopis s frekvencí připisování kupónů pololetně, je v buňce „Frekvence za rok“ uvedeno číslo 2 (2.). Počet period je automaticky vypočten na hodnotu (5*2) 10. Poslední, co zadám do připravené tabulky je kupónová sazba dluhopisu, tak jak je vyznačena v platformě, v mém případě u dluhopisu Ford činí 6,625 % p.a. (3.). Výpočet mi ukazuje, že pravidelný pololetní kupón (Kupón za periodu) bude činit 33,125 USD. Celkovou kalkulaci mi umožní excelovská funkce =ÚROKOVÁ.MÍRA (4.), jejímiž argumenty jsou (počet period; kupón za periodu; aktuální cena se znaménkem mínus; Face Value; 0). Toto zadání mi vypočítá YTM, tedy výnos do splatnosti dluhopisu podle mého velmi zjednodušeného zadání. Mohu tak konstatovat, že pokud nakoupím tento dluhopis Ford skutečně za cenu 1042,50 USD, mohl bych, při kupónových platbách, které budu reinvestovat (tedy neutrácet), vydělat na tomto držení dluhopisu do jeho splatnosti částku představující zhodnocení vložené investice na úrovni 5,638% p.a.

   Je to zcela přesné? Ne zcela, proto jsem také výše uvedl, že se jedná o zběžný výpočet YTM a opravdu mohu ve zcela hrubých obrysech takto o výnosu uvažovat. Problémem, se kterým tato úvaha nepočítá, je rozložení kupónových plateb s přihlédnutím k datu pořízení dluhopisu. Pohledem do analytické platformy mohu zjistit, že kupóny se vyplácejí v těchto termínech:

   Je 25.1.2023 a nejbližší výplata kupónu dluhopisu Ford je 15.února 2023, tedy za 21 dnů. Předchozí „zběžný“ výpočet počítal s tím, že jsem kupón obdržel přesně za půl roku od nákupu dluhopisu, další kupón za rok atd.., toto je však nepřesná nebo velmi zjednodušená úvaha, protože do výplaty prvního kupónu mi zbývá pouze 21 dnů (nikoliv tedy zjednodušeného půl roku) a další kupónová platba se uskuteční 15.8.2023, poté budou následovat další pravidelné platby kupónů až do maturity dne 15.2.2028. Co tím chci naznačit? Inkasovat vyznačený kupón má ten držitel dluhopisu, který je jeho vlastníkem v okamžiku rozhodném pro jeho výplatu. Nákupem dluhopisu, který má půlroční frekvenci vyplácení, si dnes, jedenadvacet dnů před nejbližší výplatou, zajistím jeho inkaso v plné výši, přestože jej budu držet jen 21 kalendářních dnů, a nikoliv celý půlrok jako ve zjednodušeném výpočtu výše. Bylo by ale asi podivné, kdyby se prodejce dluhopisu zbavoval těsně před jeho výplatou a daroval tak téměř celou kupónovou půlroční výplatu novému vlastníkovi. Jak to tedy funguje?

Accrued Interest a Clean Price

   Výše popsaná situace, tedy nákup kupónového dluhopisu mezi periodami výplaty kupónu, je samozřejmě ošetřena. Nemůžu se tedy spoléhat, že zachytračím a takticky nakoupím dluhopis před výplatou kupónu, slíznu smetanu a prodejce dluhopisu vyjde naprázdno. Jak to funguje ukážu na zcela praktickém příkladu, kdy jsem na svůj obchodní účet nakoupil právě tento dluhopis společnosti Ford. Na obrázku níže je vidět aktuální cenovou nabídku ze dne 25.1.2023.

   Mohu pozorovat, že aktuálně mohu dluhopis pořídit za 104,75% Face Value, tedy za 1047,50 USD za jeden kus. Na obrázku níže je zadaný příkaz k nákupu za Ask cenu.

   Pro každý dluhopis je definovaná jiná velikost nejmenšího lotu, který mohu pořídit, v případě dluhopisu Ford mohu nakoupit nejméně pět kusů (červená šipka). Takto zadávám příkaz do platformy, aby jeho výsledkem bylo pořízení těchto dluhových cenných papírů.

   Výsledkem je pořízení pěti dluhopisů společnosti Ford, každý s průměrnou cenou se započítanými poplatky za obchod ve výši 1048,50 USD. Pokud jsem tedy zaplatil za nákup každého dluhopisu -1.00 USD na komisích, opravdu jsem dluhopis nakoupil za Ask cenu 1047.50 USD, tak jak jsem požadoval.

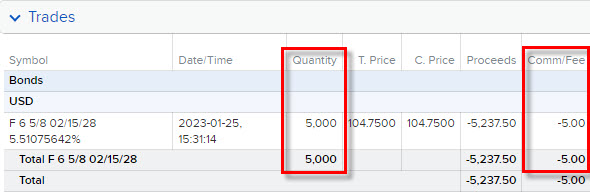
   Na obrázku výše celá situace ze statementu mého obchodního účtu, pět dluhopisů, zaplacených pět dolarů poplatků, opravdu jsem tedy pořídil tyto dluhopisy za -1047.50 USD každý. Této ceně se říká Clean Price. Tato cena ale nepředstavuje všechny náklady, které mě tento dluhopis stál, je totiž očištěna právě od nahromaděné částky úroků z nejblíže splatného kupónu, která mi nepatří a která náleží prodejci dluhopisu. Je pravdou, že za 21 kalendářních dnů (15.2.2023) inkasuji celou pololetní kupónovou výplatu ve výši +33.125 USD, budu totiž v danou chvíli držitelem dluhopisu, nicméně valná část této sumy mi nepatří, protože předcházející vlastník dluhopisu jej držel téměř po celou dobu této výplatní periody, tedy konkrétně (16.8.2022 – 25.1.2023) dobu v délce 162 dnů. Naběhlý úrok za období, kdy dluhopis nevlastním, bývá označován termínem Accrued Bond Interest a je po zobchodování dluhopisu jeho novému nabyvateli zaúčtován a patřičně sražen, aby byl předán jeho předchozímu držiteli. Na obrázku níže je vidět jeho celková hodnota pro mnou pořízených pět dluhopisů Ford:

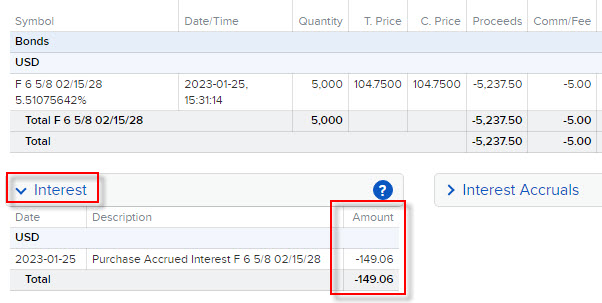
   Mohu vypozorovat, že mi bylo z mého účtu strženo -149,06 USD s komentářem Purchased Accrued Interest, tedy zaplatil jsem za pět dluhopisů jeho předcházejícímu držiteli tyto peníze a představují částku (-149,06 USD/5) ve výši -29.812 USD na jeden dluhopis Ford. Platí, že Clean Price + Accrued Interest = Dirty Price, takto se pak označuje konečná pořizovací cena dluhopisu, která představuje cenu, kterou nevidím ve své obchodní platformě, protože k ní musím připočítat ještě hodnotu naběhlých úroků, které mi nepatří a které budu muset předchozímu vlastníkovi odevzdat. Pokud bych tento dluhopis prodával, mohu pak se stejnou logikou očekávat, že kromě prodejní ceny obdržím na svůj účet také část úroků, které odpovídají době, po kterou jsem dluhopis držel a měl nárok na příslušnou část kupónového úroku.

   Jak byla hodnota Accrued Interest stanovena lze vypočítat poměřením délky kupónové periody a délky nároku na odpovídající úroky. V mém konkrétním případě je délka periody pololetí, takže při konvenci 30/360 (rok pro korporátní dluhopisy má 360 dnů, pololetí 180 dnů) činí tato délka 180 dnů. Nenáleží mi kupónový úrok za období, kdy jsem nebyl vlastníkem dluhopisu, tedy za období od předcházející výplaty do dne pořízení dluhopisu (16.8.2022 – 25.1.2023), tedy konkrétně za 162 dnů (počítá se ode dne následujícího po výplatě předcházejícího kupónu 15.8.2022, v mém případě tak od 16.8.2022). Potom, při kupónové výplatě +33.125 USD připadající na celé toto pololetí, mi nepatří částka (+33.125 USD/180)*162 = 29.8125 USD pro každý nakoupený dluhopis Ford. Pro pět nakoupených dluhopisů je mi pak strženo (5*29.8125 USD), což je částka -149,0625 USD, tedy přesně stržená suma, která je k vidění výše na obrázku z výpisu z mého obchodního účtu. Mohu tak ve shrnutí konstatovat, že jsem za každý dluhopis zaplatil o 29,8125 USD více, nekoupil jsem jej tak za cenu Ask (-1047,50 USD), kterou jsem zadal do obchodní platformy, ale kompletní pořizovací cena (Dirty Price) je tak (-1047,50 USD cena Ask – poplatek 1.00 USD – odevzdané úroky -29.8125 USD) celkově ve výši -1.078,313 USD.

   Můžu tak svůj výpočet YTM více upřesnit a použít k němu excelovskou pomůcku pro výpočet vnitřního výnosového procenta, tak jak bylo popsáno v článcích dříve. Excelovský výpočet je na obrázku níže.

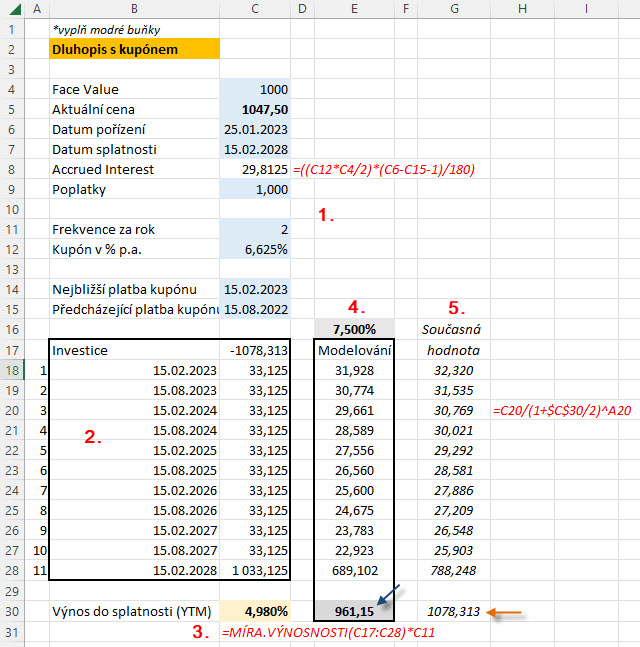
   V části (1) jsou zadány do modrých buněk parametry dluhopisu, tak jak je mohu vypozorovat z obchodní platformy. Je zde vypočítána na řádku č.8 hodnota naběhlého úroku (Accrued Interest), která mi nepatří. V části (2) jsou zapsány všechny budoucí peněžní toky spojené s držením dluhopisu, v řádku „Investice“ je již spočítána celá vstupní investice do dluhopisu, tedy Clean Price + poplatek za pořízení + Accrued Interest. Následují všechny kupónové platby, které přijmu na svůj účet společně s výplatou Face Value u maturity. Všechny tyto položky jsou sumarizovány pomocí excelovské funkce =MÍRA.VÝNOSNOSTI (3) do hodnoty Vnitřního Výnosového Procenta, které stanoví hodnotu očekávaného výnosu do splatnosti (YTM), protože se jedná o pololetní frekvenci budoucích toků, je vypočítaná hodnota YTM v tomto vzorci násobena počtem period za rok (hodnotou 2). Mohu tak vypozorovat, že vypočítaný YTM je 4.980% p.a., takové zhodnocení bych pak mohl od svého dluhopisu očekávat při splnění podmínek, které výpočet respektuje. V sekci označené (4) a popsané jako „Modelování“ mohu zadávat do šedě podbarvené buňky hodnotu YTM, kterou bych si přál dosáhnout a při jaké pořizovací ceně (modrá šipka) by se mi toto vyplnilo. Pokud bych tedy chtěl od tohoto dluhopisu Ford, aby mi vynesl 7.5 % p.a., musel bych jej pořídit za -961.15 USD. Část (5) označená jako „Současná hodnota“ je pak kontrolním výpočtem, který diskontuje všechny budoucí peněžní toky k datu výpočtu YTM do současné hodnoty dluhopisu, musí tedy platit, že součet těchto diskontovaných cen (hnědá šipka) se musí rovnat hodnotě mé investice do pořizovaného dluhopisu vyznačeného v řádku „Investice“. Celý tento Excel si můžete stáhnout v diskuzním fóru ve vlákně k tomuto článku.

   Výpočet zhodnocení mé investice do její splatnosti (YTM) je tak +4.980% p.a. Jak mohu tuto skutečnost interpretovat a jakým způsobem ji dosáhnu? Dosáhnout takového zhodnocení vyžaduje splnění třech základních podmínek a z jejich dodržení vyplyne, že vypočítaný YTM je pouze hodnotou, která odráží očekávání takového zhodnocení a nikoliv jeho přesného určení tak, jak ve skutečnosti v budoucnosti nastane. Pro dosažení hodnoty zhodnocení ve výši +4.980% p.a. musí být splněno:

   1/ Budu držet dluhopis až do jeho splatnosti. Nebudou mě tak zajímat cenové pohyby způsobené tržními vlivy (pohyb úrokových sazeb na dluhopisových trzích apod.). Je patrné, že pokud bych prodal dluhopis před jeho splatností za vyšší cenu než jsem jej koupil, mohu utržit mimo již přijaté kupóny další kapitálový výnos a hodnotu projektovaného YTM mírně vylepšit a naopak, při jeho prodeji za nižší než pořizovací cenu toto YTM snížit.

   2/ Budu reinvestovat všechny obdržené kupóny, a to okamžitě po jejich obdržení.

   3/ Reinvestice kupónů se bude provádět s úrokovou sazbou rovnající se vypočítanému YTM (+4.980%). Nemohu odhadnout, jaké budou aktuální příležitosti úročení na trzích pevně úročených cenných papírů v horizontu několika let, které představuje držení mého dluhopisu Ford se splatností v roce 2028. Jedno je jisté, pokud by se mi podařilo inkasované kupóny zhodnocovat vyšší sazbou než +4.980% p.a., dosáhnu celkově vyšší zhodnocení mého dluhopisu než jsem si nyní vypočítal a naopak, pokud se mi toto postupné zhodnocování nebude dařit za podmínek vypočítaného YTM, dosáhnu celkově nižšího zhodnocení, než jsem si svým výpočtem určil.  

   Z daného popisu podmínek je jasné, že splnění první z nich není nic nemožného, druhá podmínka je otázkou obchodní techniky, ovšem třetí podmínka je zcela zásadní při vyhlídkách na dosažení očekávaného výnosu. Z popsaného vyplývá, že ačkoliv nakoupím dluhopis jako „cenný papír s pevným výnosem“, nemohu jednoznačně prohlásit, kolik na této investici vydělám optikou tohoto přístupu. Není tak zcela určující, za kolik cenný papír nakoupím, jakou má hodnotu kupónu a za jak dlouho je jeho splatnost, přestože toto jsou základní faktory tvořící základ budoucího výnosu, musím ještě, při přesvědčení, že dluhopis budu držet do splatnosti, počítat s aktuálním vývojem úrokových sazeb na trzích, které určí další (a podstatný) výnos z přijatých budoucích cash flow.

YTM, kupón a cena dluhopisu

   K jednoduché interpretaci a vztahu vypočítaného YTM k aktuální ceně dluhopisu s definovaným kupónem mohu, ve světle předcházející výpočtů, zaznamenat základní pravidla, která mi pomohou se základní interpretací YTM.

   A/ Pokud je YTM nižší než hodnota kupónové sazby dluhopisu, musím očekávat, že cena dluhopisu bude vyšší než Face Value, v mém případě je vypočítaná hodnota YTM +4.980% p.a. a kupónový výnos představuje 6.625% p.a.       

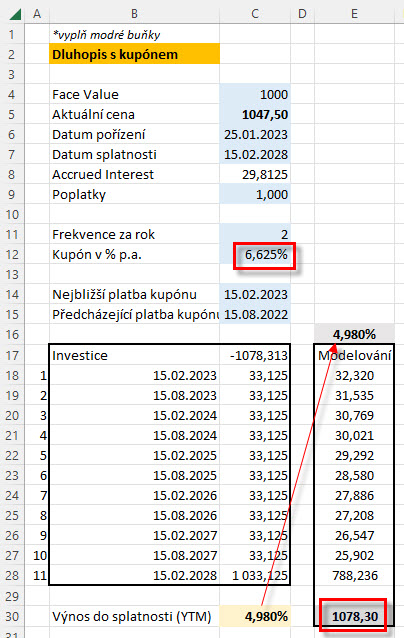
  Tato situace odpovídá mému konkrétnímu obchodu. Vysoký kupón (+6.625% p.a.) způsobuje, že se nemohu divit, že nakupuji za hodnotu vyšší než Face Value, tedy za -1.078,313 USD. Mohu také konstatovat, že pokud je cena dluhopisu vyšší než Face Value, bude YTM nižší než vyznačený úrok vyplývající z kupónu.

    B/ Pokud by hodnota YTM byla stejná, jako je hodnota kupónové sazby dluhopisu, tedy pokud by kupón měl sazbu +6.625% p.a. a stejná by byla hodnota YTM +6.625% p.a., pak bych měl tento dluhopis být schopen nakoupit přesně za Face Value.

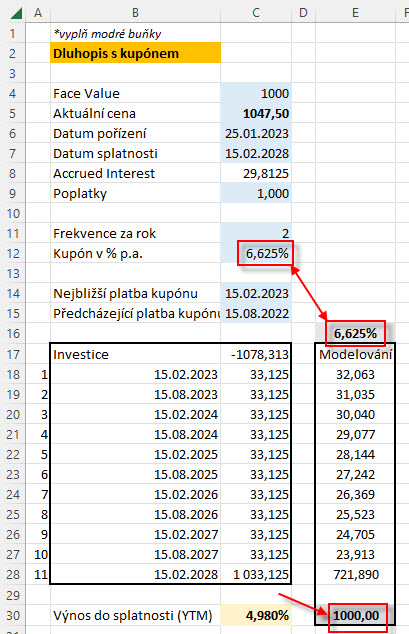
   Jinými slovy, pokud se dluhopis nabízí za Face Value, jeho YTM bude rovna úrokové sazbě odpovídající vyznačenému kupónu.

   C/ Pokud je YTM vyšší než hodnota kupónové sazby dluhopisu, musím očekávat, že cena dluhopisu bude nižší než Face Value, v mém případě si mohu namodelovat vypočítanou hodnotu YTM například na +8.00% p.a. při kupónovém výnosu představujícím +6.625% p.a.       

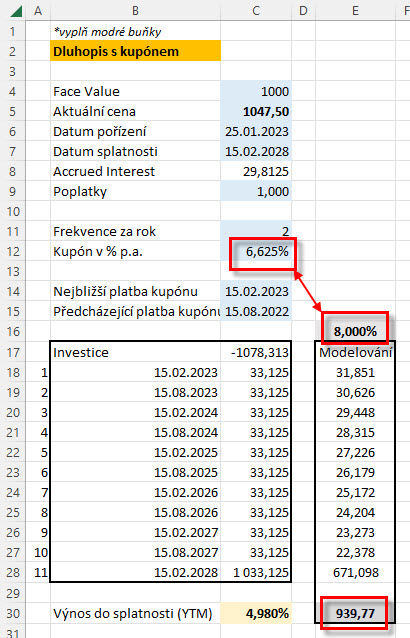
   Opět by mělo platit, že pokud budu pozorovat cenu sledovaného dluhopisu a tato bude nižší než Face Value, mohu očekávat YTM vyšší, než je vyznačená kupónová sazba. V konkrétním modelovém příkladu je při kupónu +6.625% p.a. a vypočítaném modelovém YTM na úrovni +8.00% p.a. patrné, že dluhopis by měl stát méně než 1.000 USD, konkrétně pouze 939,77 USD.

   Změřit výnos dluhopisu je celkem výzva a nabízejí se nejrůznější metody, jak se k takovému výpočtu postavit. Mohu si samozřejmě vymyslet jiné způsoby, jak se k celkovému výnosu dobrat, důležité ale z mého pohledu je pochopit základní princip takového ocenění a tento pak dále rozvíjet. Mohu využít vysoce sofistikované cenové modely, mohu využít publikované internetové kalkulátory nebo si vymyslet svůj vlastní výpočet například pomocí VBA skriptu zdokonalujícího uvedený excelovský výpočet, mohu celý výpočet svěřit vlastnímu naprogramovanému řešení, základní úvaha a principy budou ale patrně vycházet ze stejných základů, které byly popsány výše…:c)       

   Komentáře a příspěvky k tomuto článku prosím směrujte do Diskuzního fóra do tohoto vlákna, zde také najdete ke stažení excelovský sešit, ze kterého jsou ukázky k tomuto článku  :c)