V hrnci dluhopisových trhů to začíná pěkně bublat. Pryč jsou doby nevýznamných výnosů či dokonce záporných úrokových sazeb, investoři začínají větřit zajímavé příležitosti a po dlouhá léta přehlížený segment cenných papírů s pevným výnosem začíná nabírat na zasloužené pozornosti. Následující řádky dalšího dílu dluhopisového seriálu pak budou o projasnění některých problémů spojených s pořízením dluhových cenných papírů a snad pomůžou vyřešit alespoň některá základní dilemata, se kterými může dluhopisový investor při vstupu na toto velkolepé investiční tržiště zápasit.
Nepochybuji, že investor do dluhových cenných papírů má svůj základní náhled na vývoj úrokových sazeb, který vychází z alespoň zevrubného poznání aktuálního tvaru výnosové křivky dluhopisů, které jsou benchmarkem pro trh, na kterém chce svou investici umístit. To, jestli jsou aktuální výnosy vyšší u dluhopisů s kratší splatností než u dluhopisů se vzdálenější splatností (méně častý jev viz článek Dluhopisy – X.) nebo běžnější tvar výnosové křivky, kde jsou výnosy vyšší ve vzdálenějších splatnostech než ve splatnostech kratších (stoupající nebo plochý tvar křivky), by mělo být základní výbavou pro rozhodování, jak budu svou investici do dluhopisů koncipovat. Poznání tvaru výnosové křivky a náhled na vývoj úrokových sazeb by pak měl být základním předpokladem, jak k takové investici přistoupit a mohl by se promítnout do prvního „rozhodovacího problému“.
Najednou nebo nadvakrát…?
Pohledem na dluhopisový trh s nabídkou nejrůznějších splatností, výnosů a kupónů mohu začít přemýšlet, jak se zamýšlená investice bude vyvíjet v budoucnosti, zejména například s ohledem na charakter a stav aktuálních výnosů odrážející tvar výnosové křivky benchmarkových cenných papírů. Mé základní dilema by pak mohlo být například takový tvar: „Mám investovat do ročního dluhopisu s výnosem 5% p.a. nebo se mi vyplatí investovat do dluhopisu s půlroční splatností s výnosem 4.8% a poté investovat do dalšího půlročního dluhopisu?“ Tato základní obchodní úvaha vychází z předpokladu, že neznám vývoj výnosů do budoucnosti a mohu tak předpokládat, že výnosy porostou a budu moci při investici do kratšího dluhopisu tuto reinvestovat za vyšší výnosy po jeho splatnosti nebo naopak přijmu riziko, že při poklesu výnosů se mi již nepodaří za aktuální výnosy v budoucnosti mou investici zhodnotit, toto vše při sázce na „drobení investice“ do kratších časových intervalů. Mohu ale také usoudit, že zafixovat si výnos na delší dobu volbou dvojnásobně dlouhou investicí za pevně stanovený aktuální výnos je pro mě lepší volbou, jsem totiž přesvědčen, že výnosy již dále neporostou, a naopak mohou v horizontu do splatnosti dluhopisu naopak klesnout. Jak mohu tento proces kvantifikovat? Bude mě zajímat, jaký budoucí výnos za půl roku bude pro mě „BreakEven“ pro krátkodobější dluhopisovou investici za půl roku, aby zaručoval výnos vyšší než dlouhodobější roční investice.
Pokud investuji do dluhopisu s půlroční nejběžnější frekvencí připisování úroků, tak mohu u investice do ročního dluhopisu s výše uvedeným výnosem 5% p.a (yrok). konstatovat, že tento výnos bude (viz postup v článku Dluhopisy – I.):
![]()
Mocnina „na druhou“ pak reflektuje skutečnost, že doba připisování výnosu nastala v daném období dvakrát, specifikoval jsem, že se jedná o dluhopis s půlroční frekvencí inkasa vyznačeného kupónu. Ve stejném duchu pak investice do půlročního dluhopisu s výnosem 4.8% p.a.(ypůlrok) bude mít tento tvar:
![]()
Pokud budu chtít vyhodnotit, jaký výnos musí po uplynutí půlročního období splatnosti půlročního dluhopisu být na trzích k dispozici, abych získal stejný výnos jako při investici do ročního dluhopisu, musím obohatit vypočítané půlroční zhodnocení o hledání výnosu, který mi bude reflektovat zhodnocení investice v dalším půlroce na takové úrovni, abych dosáhl na zhodnocení stejné jako při investici do jednoročního dluhopisu:
![]()
Hledání hodnoty výnosu (z) potřebného za půlroku k tomu, abych dosáhl zhodnocení alespoň takového, jako je přímá investice do jednoročního dluhopisu, je pak jen otázka jednoduché algebry:
![]()
Pokud je hodnota investice (Investice) stejná, je potom hledanou hodnotou potřebného výnosu (z) tento konečný upravený tvar výše uvedené rovnice:
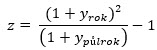
Konkrétně v mém modelovém příkladu, výnos půlroční investice s ročním výnosem 4.8% p.a. představuje zhodnocení 2.4% (ypůlrok). Roční výnos 5% představuje půlroční zhodnocení 2.5% (yrok), potom:
![]()
Zhodnocení dalšího půlroku (z), tak musí představovat výnos nejméně 2.60009%, což představuje investici do druhého půlročního dluhopisu s vyznačeným ročním zhodnocením ve výši nejméně 5.20018% p.a. potřebného k tomu, abych dosáhl rozložením investice do dvou pololetí na stejné zhodnocení, jako v případě investice na jeden rok.
Pokud tedy nyní pozoruji výnosy jednotlivých dluhopisů podle jejich splatnosti, měl bych ve světle výše uvedeného výpočtu předpokládat, že pro dosažení vyššího výnosu z krátkodobých půlročních investic potřebuji, aby výnosy půlročních dluhopisů přinesly vyšší výnos (5.20018% p.a.) než nyní (4.8% p.a.) a mohly tak přinést stejné nebo vyšší zhodnocení, jako představuje investice do ročního dluhopisu. Pokud bych byl vystaven takto strukturovanému dilema o investici do krátkodobých nebo dlouhodobějších dluhopisů, mé predikce úrokových sazeb by se pak měly odvíjet od výše uvedeného zjištění.
Průměrná doba do splatnosti a Durace
Výnosy dluhopisů v době, kdy píšu tento článek, závratně rostou a s tímto růstem také odpovídajícím způsobem roste počet otázek, jak takový růst zobchodovat. Odpověď je celkem jednoduchá – mnoha způsoby :c). Stejně jako investor do akcií, stojí před dluhopisovým investorem úkol vyhodnotit, do jakých titulů má aktuálně investovat a co od takové investice očekávat. Odpovědi na tyto otázky pak budou patrně ležet na investorově rozpoložení, povaze a pohledu na podstatu provedené investice. Originalita každého obchodníka se patrně stejně originálně projeví také v investičním přístupu, bude tak podstatné, jaké primární očekávání je s touto investicí spojeno a jak může výběr dluhového investičního nástroje pomoci toto očekávání splnit. Pokud se rozhoduji pořídit dluhopis, musím patrně provést nějaký vnitřní rozhodovací proces, jak by mělo toto pořízení vypadat a které dluhopisy mi pomohou tento rozhodovací proces vyřešit.
Chci dluhopisový výnos, který vyplyne z držení dluhopisu do splatnosti bez ohledu na okolnosti, které budou na trzích panovat nebo chci pojmout dluhopisovou investici jako spekulaci spojenou s pohybem ceny tohoto cenného papíru? Zajímá mě pravidelné kupónové cash flow nebo chci všechny nevýhody spojené s tímto přístupem nahradit investicí do bezkupónového dluhopisu? Chci být v investici velmi dlouhou dobu nebo je mi vlastní krátkodobé reinvestování do dluhopisů s ultrakrátkou dobou do splatnosti? Jistou porci odpovědí na tyto otázky lze nalézt v článku Dluhopisy – VIII., pokusím se nyní tam popsaná zjištění nyní znovu formulovat do odpovědí na výše popsané otázky a vyřešit tak dilemata, které tyto otázky navozují.
Kupónový dluhopis
K nákupu kupónového dluhopisu za určitou cenu mě může vést rozhodnutí vyplývající z vyznačeného výnosu do splatnosti (YTM). Podstata jeho výpočtu je popsána v článku Dluhopisy – V., když základním poznáním podstaty tohoto výpočtu je zjištění, že se na něj nemohu zcela spolehnout. Přestože by výnos do splatnosti měl být jedním ze základních rozhodovacích prvků, jeho podstata trpí zejména reinvestičním rizikem.

Na obrázku je příklad dluhopisu společnosti Metlife (MET) (1) se splatností 15.12.1936 nesoucí kupón ve výši 6.4% p.a. (2), který je splatný pololetně (3) a jeho CUSIP je 59156RAP3 (4). Tento dluhopis mohu pořídit za Ask cenu 96,1540% z Face Value (při investici 1.000 USD vynaložím 961.540 USD) (5) a pořízení za tuto Ask cenu odpovídá Yield To Maturity (dále jen „YTM“) ve výši 6.846% p.a. (6). Tento (nebo vyšší) výnos do splatnosti během třináct let jeho držení obdržím ale pouze v jediném případě, a to za podmínky, že se mi podaří utržené kupóny reinvestovat ihned po jejich inkasu s úrokem ve výši YTM, tedy alespoň za 6.846% p.a. Splnění této podmínky je ale nejisté, protože nemohu nijak předpokládat, že se mi podaří takový úkol úspěšně realizovat, třináctileté období je dostatečně dlouhé na to, abych mohl úspěšně předpokládat, že na trzích budou příležitosti takto stanoveného zhodnocení. Musím tedy zaměřit pozornost na takové parametry nakupovaného dluhopisu, které nebudou závislé na budoucím vývoji úrokových sazeb a budou vhodně popisovat dluhopis bez tohoto základního reinvestičního rizika spojeného s YTM.
Mohu tak nyní přesně pouze vědět, že dluhopis MET pořídím za 961.54 USD a tento dluhopis mi přinese každého půl roku kupón (6.4%/2) ve výši 3.2% z hodnoty Face Value. Rozložení kupónových plateb mohu odečíst z bond screeneru mého brokera:
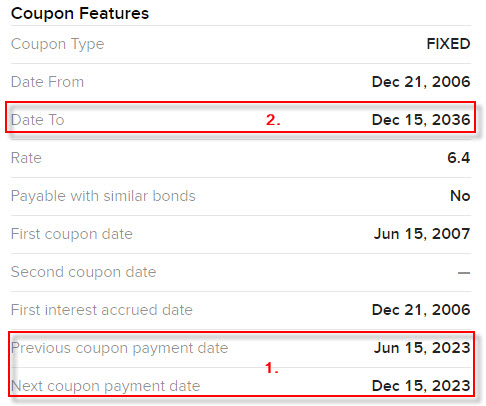
Dluhopis vyznačený kupón vyplácí každého 15.7. a 15.12. doby do splatnosti dluhopisu (1), poslední splátka kupónu je u maturity dluhopisu, tedy 15.12.2036 (2), pracuji tedy s třináctiletým kupónovým dluhopisem.
Bez ohledu na YTM mohu nyní z údajů o tomto dluhopisu vyčíst, že tento bude pro mě zdrojem příjmů z kupónů a dluhopis kupuji za cenu nižší, než je Face Value. Protože průběžné kupónové platby nejsou malé, ale představují příjem 32 USD každý půlrok držení dluhopisu a navíc jsem dluhopis koupil s diskontem k Face Value, mohu ve zjednodušení konstatovat, že dluhopis se mi „splatí dříve“, než v den jeho splatnosti, návratnost vynaložených prostředků tak teoreticky nastane dříve než u Maturity Date. Výpočet průměrné doby, do které mohu mluvit o splatnosti dluhopisu, je určením tzv. „průměrné doby do splatnosti dluhopisu“ a mohu již nyní, bez ohledu na techniku výpočtu odhadnout, že pokud bude mít dluhopis vysoký kupón, bude tato průměrná doba do splatnosti nižší (dostanu své vložené peníze zpět dříve) než by tak bylo u stejného dluhopisu s podstatně nižším kupónem. Průměrná doba do splatnosti dluhopisu je vypočtena jako součet váhy každé budoucí platby kupónu a závěrečné splátky Face Value v jejich současných hodnotách. Pokud jsem se ve výpočtu v článku Dluhopisy – V. snažil najít hodnotu YTM, tedy hledat takovou úrokovou sazbu, která diskontováním všech budoucích cash flow z dluhopisu a jejich následným součtem vygeneruje aktuální cenu dluhopisu, potom, pokud jsou všechny tyto budoucí cash flow platby zváženy podle jejich hodnoty a poměřeny s aktuální hodnotou dluhopisu – tento výpočet vypočítá právě průměrnou dobu do splatnosti dluhopisu. V článku Dluhopisy – VIII. je tento postup výpočtu popsán a označen za tzv. Macaulayovu Duraci, jedná se tak o stejný početní postup, jenom bych mu nyní dopřál větší pozornosti. Macaulayova Durace a průměrná doba do splatnosti dluhopisu je tedy stejná věc, poměřuji součet budoucích diskontovaných cash flow s aktuální cenou dluhopisu, z daného poměru pak vyplývá, že kratší průměrnou dobu do splatnosti (nižší Macaulayovu Duraci) bude mít dluhopis, který má (při jinak stejných parametrech) vyšší kupón. K důkazům této závislosti jsem použil vlastní excel, který je schopen simulovat tyto (a další později v článku popisované) situace:
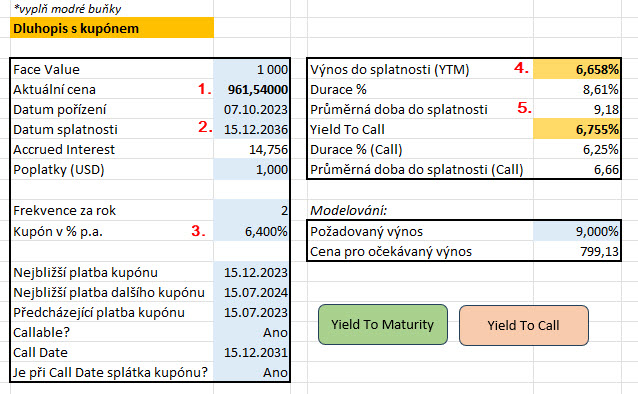
Při aktuální ceně 961.54 USD (1) má dluhopis se splatnosti třináct let (2) a kupónem 6.4% p.a. (3) vypočítaný výnos do splatnosti (YTM) ve výši 6.658% p.a. (4) a průměrnou dobu do splatnosti 9.18 let (5). Výpočet získám zadáním údajů do modrých buněk excelu a po stisknutí tlačítka „Yield To Maturity“ se spustí makro, které vytvoří „budoucnost dluhopisu“ a provede potřebné výpočty:
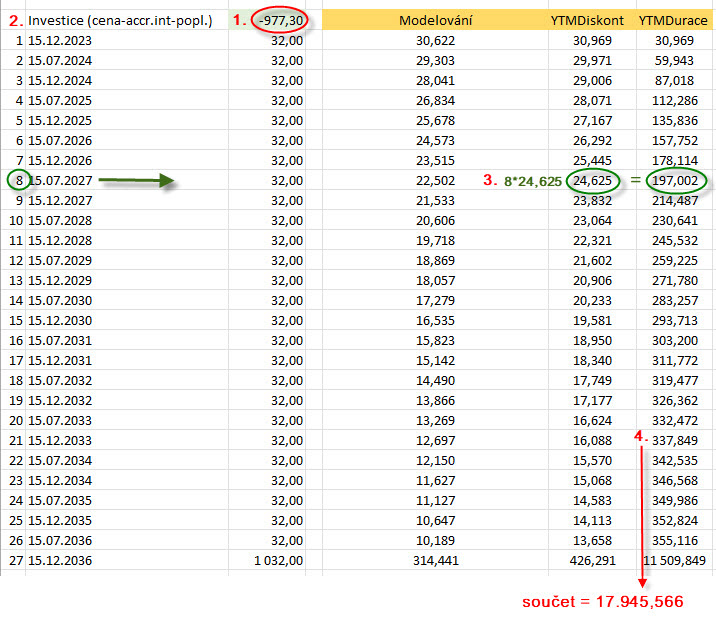
K pořizovací ceně dluhopisu se přičte hodnota úroku z kupónu za období, po které nejsem jeho vlastníkem (Accrued Interest) a komise mého brokera, takže skutečná pořizovací cena je nyní -977.30 USD (1). V prvním sloupci excelu (2) mohu vidět, že nakoupený dluhopis mi připraví celkem 27 budoucích peněžních toků z kupónových plateb po 32.00 USD a konečné splátky Face Value ve výši 1.000 USD. Mohu pak ve sloupci YTMDiskont pozorovat vypočítané diskontované hodnoty jednotlivých budoucích plateb podle vypočítaného výnosu do splatnosti, například v případě osmého toku v pořadí označeného zeleným kroužkem činí dnešní diskontovaná hodnota kupónu ve výši 32 USD splatná 15.7.2027 částku 24.625 USD (3). Pro potřeby výpočtu průměrné doby do splatnosti je této částce přisouzená váha svého budoucího pořadí (tedy hodnota 8) a touto vahou je takto diskontovaný kupón vynásoben. Součet všech takto zvážených diskontovaných částek je pak 17.945,66 (4). Nezbývá pak, než tento výsledný součet (4) porovnat s pořizovací cenou dluhopisu (1) a zjistit (17.945,66/977.30 = 18.36), že průměrná doba do splatnosti tohoto dluhopisu (výsledek musím dělit dvěma – jedná se o pololetní připisování kupónů) je opravdu (18.36/2) deklarovaných 9.18 let. Z uvedeného výpočtu je pak jasně patrné, že při nižším kupónu (diskontované cash flow bude mít v jednotlivých položkách vyšší hodnoty) budu poměřovat s aktuální cenou dluhopisu (977.30 USD) vyšší částku v čitateli výpočtu a celková průměrná doba do splatnosti se tak bude zvyšovat. Mohu tak například při stejných okolnostech zadat výpočet průměrné doby do splatnosti dluhopisu pro zadaný třináctiletý dluhopis MET kupón pouze ve výši 2% p.a. a pozorovat, jak se prodlouží průměrná doba do splatnosti takto upraveném, sníženém kupónu:
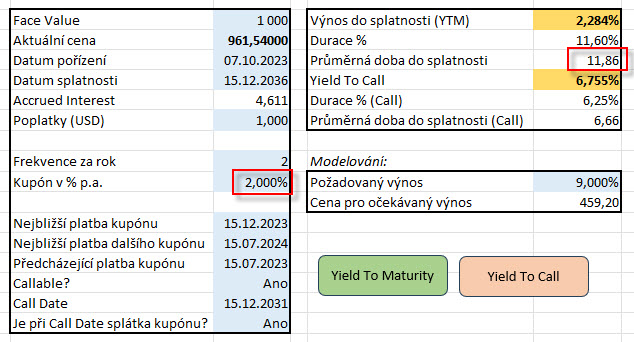
Nižší kupón znamená menší budoucí cash flow a prodlužující se průměrnou dobu do splatnosti, mohu pak pozorovat, že kupón ve výši 2% p.a. způsobil prodloužení průměrné doby do splatnosti na 11.86 let.
Zdá se, že je to logické zjištění a pokud jsem rozhodnutý držet dluhopis do splatnosti, je mi celkem jedno, jaká je průměrná doba do splatnosti. Proč to tedy vlastně hraje nějakou významnou roli? Význam průměrné doby splatnosti je směrodatná hodnota, která určuje citlivost dluhopisu na změnu úrokové sazby, a to je hlavní podstata nutnosti jejího vnímání. V článku Dluhopisy – VIII. jsem již popisoval, že pokud poměřím hodnotu Macaulayovy Durace (tedy vlastně průměrné doby do splatnosti) s aktuálním výnosem dluhopisu, mohu získat tzv. Modifikovanou Duraci, obecně popisovanou pouze jako „duraci“, tedy kvantifikování reakce změny ceny dluhopisu na změnu jeho výnosu.
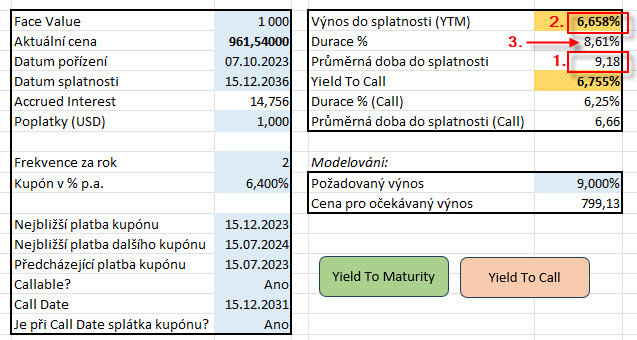
Poměřením průměrné doby do splatnosti dluhopisu, tedy Macaulayovy Durace, ve výši 9,18 (1) s vypočítaným výnosem do splatnosti ve výši 6.658% p.a. (2) zjistím duraci mého třináctiletého dluhopisu (9.18/1.06658) s hodnotou 8.61% (3). Mám tak zjištěno, že pokud se změní výnos dluhopisu o +1.00%, potom klesne cena mého dluhopisu o -8.61%. Pochopení této souvislosti je jedno z nejpodstatnějších k pochopení, jak vybírat dluhopis v souvislostí s očekávanou změnu výnosů dluhopisů. Protože citlivost dluhopisů na změnu úrokových sazeb a potažmo výnosů dluhopisů (durace) je dána podílem průměrné doby do splatnosti a výnosem dluhopisu, je z charakteru podílu zřejmé, že čím delší bude průměrná doba do splatnosti dluhopisu, tím bude citlivost na změnu výnosu (durace) vyšší. Na změnu výnosů (například růst) tak budou reagovat více dluhopisy s delší průměrnou dobou do splatnosti (jejich cena více klesne) než bude reakce dluhopisů s kratší dobou do splatnosti. Pokud budu mít na svém účtu pořízeny dva dluhopisy se stejnou dobou do splatnosti a přibližně stejnou pořizovací cenou, citlivější na změnu výnosů (vyšší duraci) budou mít dluhopisy s nižším kupónem, protože ten dluhopis, který má stejné parametry, ale nižší kupón, má delší průměrnou dobu do splatnosti, tato průměrná delší doba do splatnosti pak vstupuje do popisovaného vzorce durace, do jeho čitatele, s vyšší hodnotou při stejném jmenovateli a způsobuje tak vyšší hodnotu vypočítávané durace.
Mohu si opět provést demonstraci s třináctiletých dluhopisem MET, kterému při stejných parametrech snížím kupón na úroveň 2% p.a.,
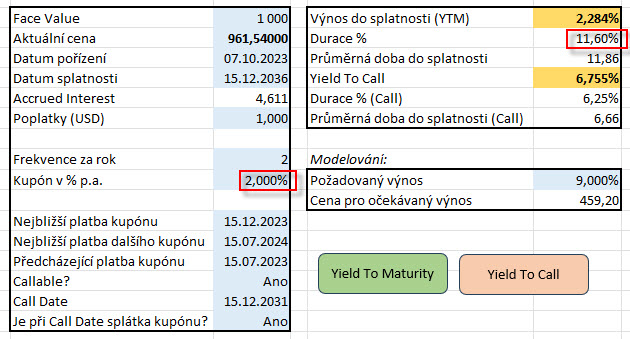
Snížení kupónového výnosu ze 6.4% p.a. na úroveň 2% p.a. způsobilo nárůst durace dluhopisu z 8.61% na 11.60%. Musím tak počítat, že jedno procento růstu výnosu dluhopisu srazí jeho cenu o -11.60%. Mohu se tak nyní pokusit vyřešit první dilema, kterým by mohlo být váhání, jakou investici s dluhopisem vlastně provést. Pokud budu chtít pojmout dluhopisovou investici jako dlouhodobou záležitost a je mi celkem jedno, jestli se cena dluhopisu bude nějak pohybovat, potom se mohu při investici do dluhopisu drženého do splatnosti zaměřit na jeho výnos a tento si připravit investicí do dluhopisu za dobrou cenu s odpovídajícím kupónem. Pokud chci dluhopisovou investici pojmout jako investici do ceny dluhopisu a požadovat z tohoto obchodu kapitálový výnos spojený se změnou jeho ceny, měl bych se zaměřit na dluhopisy s vyšší durací, toto by mělo, v případě pohybu úrokových sazeb s odpovídající změnou výnosu drženého dluhopisu, přinést kýžený pohyb ceny samotného dluhopisu a přinést kapitálový výnos vyplývající z této změny.
Pro ilustraci mohu ukázat čtyři třicetileté americké vládní dluhopisy s položením otázky, který z nich se nejvíce hodí na dlouhodobé držení nebo spekulaci na pohyb jeho ceny:

Čtyři třicetileté dluhopisy byly emitovány postupně v květnu 2020, 2021, 2022 a 2023. Přestože je splatnost každého z nich vždy o jeden rok delší a mají téměř identický YTM ve výši kolem 5% p.a. (zelený rámeček), zcela diametrálně se liší jejich aktuální cena. Mohu pozorovat, že první dluhopis se splatností v roce 2050 a s kupónem pouze 1.25% p.a. se dá pořídit za 44.888% z Face Value, dluhopis s nejstarší splatností o tři roky později v roce 2053 již nese kupón 3.625% p.a. a jeho aktuální cena představuje 79.246% z Face Value, pořizovací ceny jsou uvedeny v červeném rámečku. Jak vypadají průměrné doby do splatnosti a durace jednotlivých dluhopisů po výpočtu v mém excelu je patrné níže:
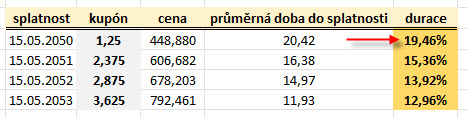
Přestože je rozdíl mezi splatností pouhé tři roky, je rozdíl v duracích dramatický a je způsoben výši vypláceného kupónu. Zatímco „nejmladší“ třicetiletý dluhopis s kupónem pouhých 1.25% p.a. má duraci 19.46%, nejstarší dluhopis s trojnásobným kupónem ve výši 3.625% p.a. má duraci 12.96%, případný pád výnosů na třicetiletých dluhopisech o -1% p.a. povede k růstu ceny dluhopisu s nejvyšší durací o závratných +19.46%. Na otázku, který z nich bych si vybral pro spekulaci na pohyb jeho ceny, je tak jasná odpověď – dluhopis s nejnižším kupónem. V případě požadavku na pořízení třicetiletého dluhopisu s cílem omezit jeho cenový pohyb do splatnosti na co nejnižší úroveň by pak patrně padla volba na dluhopis s nejvyšším kupónem.
Zerobondy
Zobecnění předchozích řádků by mohly vyznít tak, že průměrná doba do splatnosti kupónového dluhopisu je vždy kratší než doba do splatnosti tohoto dluhopisu. Přijímané cash flow v podobě kupónových plateb pak dobu do splatnosti zkracují a toto má vliv na volatilitu dluhopisu způsobenou změnou úrovně výnosů, kterou mohu měřit durací. Zerobondy, jako bezkupónové dluhopisy, ale nemají do své splatnosti žádné cash flow, pouze jediné – u splatnosti dluhopisu je investorovi splacena Face Value tohoto dluhopisu. Průměrná doba do splatnosti zerobondu je tak rovna době do splatnosti tohoto dluhopisu. Pětiletý zerobond bez kupónu má průměrnou dobu do splatnosti pět let, žádné diskontování a součet vážených diskontů poměřený s cenou dluhopisu, tento výpočet odpadá. Jak se projeví neexistence průběžného cash flow u zerobondu do durace a jeho citlivosti na změnu výnosů v praktické ukázce:

Ze screeneru v aplikaci TWS mého brokera mohu vybrat dva americké vládní dluhopisy se stejnou dobou do splatnosti, a to k 15.5.2030. Tyto zhruba šestileté dluhopisy se liší pouze tím, že první dluhopis nese kupón 6.25% p.a. (1) a jeho pořizovací cena je 1081.29 USD, kdežto druhý dluhopis je zerobond (2), který nenese žádný kupón a jeho pořizovací cena je 732.73 USD. Pro prozkoumání kupónového dluhopisu mohu použít níže uvedený obrázek:
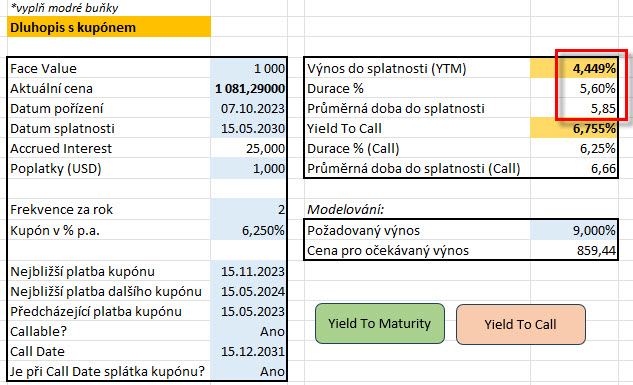
Průměrná doba do splatnosti dluhopisu s kupónem je 5.85 let a poměřením s vypočítaným výnosem do splatnosti ve výši 4.449% mohu konstatovat, že tento dluhopis bude mít duraci (5.85/1.04449) ve výši 5.60%. Citlivost na pohyb výnosu o jedno procento bude doprovázena pohybem ceny dluhopisu o +/-5.60%. Pomocí stejného excelu na listu „Zerobond“ mohu vypočítat parametry druhého dluhopisu (zerobondu):
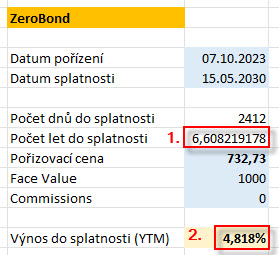
Doba do splatnosti je 6.61 roků (1) a při vypočítaném výnosu do splatnosti 4.818% p.a. (2) mohu konstatovat, že vypočítaná durace (6.60/1.04818) tohoto zerobondu bude 6.32%. Každý pohyb výnosu o jeden procentní bod pak bude doprovázen změnou ceny zerobondu +/-6.2%. Absence kupónových plateb pak způsobuje, že pokud budu chtít spekulovat na pohyb ceny dluhopisu, bude pro mě zerobond vhodnější volbou, jeho vyšší volatilita mi zaručuje lepší cenové reakce na změnu úrovně výnosů. K rozhodnutí držet zerobond do splatnosti díky „zafixování“ výnosu při jeho pořízení odejmutím reinvestičního rizika popsaného v minulém článku tak mohu připočítat jeho další vlastnost k využití – jeho vyšší citlivosti (vyšší duraci) na změnu výnosu ke spekulaci na cenový pohyb zerobondu.
Accrued Interest a poplatky
Pořízení dluhopisu s cílem dlouhodobější investice musím zařídit tak, abych na této investici co nejvíce vydělal. Přestože to vypadá, že je to nepodstatné zaobírání se detaily, musím do svých kalkulací nakládání s dluhopisem zahrnout také skutečnost, že pořízením dluhopisu v období mezi výplatou kupónů musím část naběhlých úroků z kupónu odevzdat bývalému vlastníkovi dluhopisu a také musím přihlédnout ke skutečnosti, že za dluhopis zaplatím nějaký poplatek svému brokerovi. To, že se nejedná o zanedbatelné částky, které se mohou propsat do budoucí výkonnosti mohu ukázat opět na dluhopisu MET.

Nákup dluhopisu MET (1) s kupónem 6.4% p.a. (2) prostřednictvím platformy mého brokera za cenu Ask ve výši 961.54 USD (5) avizuje výnos dluhopisu (YTM) ve výši 6.846% p.a. (6). Přestože do konstrukce a zobrazení tohoto výnosu v platformě mého brokera vstupuje ještě další skutečnost popsaná později v článku, mohu vypozorovat, že pokud si nasimuluji svůj vlastní výpočet YTM pomocí své excelovské aplikace, dostanu jiný výsledek:
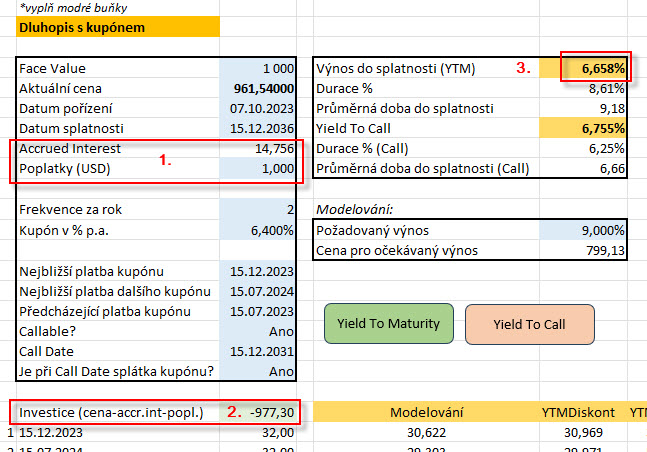
Především musím do pořizovací ceny, výdaje na nákup dluhopisu, zakomponovat náklad na část kupónové platby, která mi nepatří a poplatek, který zaplatím za dluhopisovou transakci (1). Protože kupuji dluhopis 7.10.2023 a další kupónová platby je 15.12.2023, musím odevzdat část tohoto prvního kupónu, který inkasuji, majiteli dluhopisu, od kterého jej pořizuji. V článku Dluhopisy – V. je popsáno, jak výpočet takové položky vypadá, v mém případě odevzdávám předchozímu vlastníkovi část budoucího kupónu ve výši 32 USD za období od jeho poslední výplaty 15.7.2023 do okamžiku, kdy jsem dluhopis pořídil, tedy k dnešnímu datu 7.10.2023. Z obrázku mohu vypozorovat, že tato částka činí 14.756 USD. Společně s komisí za provedený obchod ve výši 1.00 USD tak nepořizuji dluhopis za cenu uvedenou v mé platformě ve výši 961.54 USD, ale celková pořizovací cena je nyní (-961.54 USD – 14.756 USD -1.00 USD) ve výši -977.30 USD (2). Pokud do výpočtu výnosu zahrnu tyto platby, je celkový výnos do splatnosti ve výši 6.658% p.a. (3) a liší se od YTM zobrazovaného v platformě o -0.135%. Mohu pak pro zajímavost ukázat, nakolik se výpočet přiblíží hodnotě z platformy TWS, pokud do svého výpočtu Accrued Interest a poplatky vůbec nezahrnu:
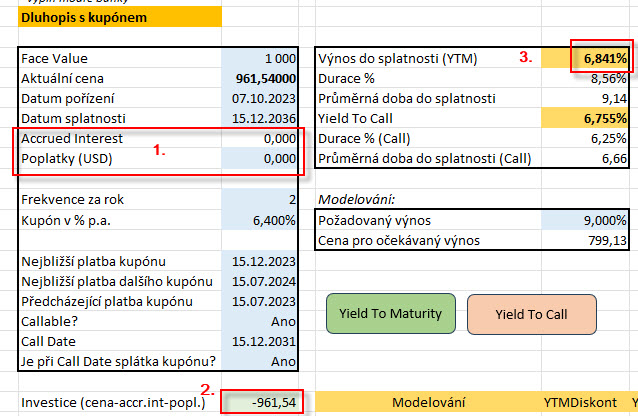
Nulový Accrued Interest a poplatky za obchod (1) způsobují, že do svého výpočtu zahrnuji opravdu pořizovací cenu -961.54 USD, kterou vidím ve své obchodní platformě (2), tyto hodnoty pak navyšují výnos do splatnosti na hodnotu 6.841% p.a. (3), což je YTM, který mi TWS aktuálně zobrazuje (6.846% p.a.).
Musím si tak uvědomit, že nákup dluhopisu podle hodnot, které mi zobrazuje má obchodní platforma, je pouze orientační a skutečné parametry provedeného obchodu se od skutečnosti, které jsem chtěl dosáhnout mohou mírně lišit. Mohu si tak pouze povzdechnout nad telefonátem jakéhosi finančního poradce, který mi nabízel dluhopisy nejmenované společnosti a za případně uzavřenou transakci „by si tedy naúčtoval 4% poplatek z objemu obchodu“….:c).
Call a detaily se svoláváním emisí
Možnost svolat emisi dluhopisu (nebo její část) svým emitentem před datem splatnosti dluhopisu jsem již popisoval v článku Dluhopisy – VII. Přestože jsem tuto problematiku již popsal, chtěl bych se zaměřit na některé její další nuance. Základním sdělením do začátku tohoto problému je konstatování, že americké vládní dluhopisy jsou dluhové cenné papíry, které nejsou „Callable“ a jejich pořízení a následné držení mi nikdo nemůže překazit, emitent – americká vláda – nemůže tyto vydané emise svolat zpět. Ve světě korporátních a municipálních dluhopisů je ale tato možnost předčasného svolání natolik významný faktor, že je nutné s ním při investici do „callable“ dluhopisů počítat. Tato „investiční komplikace“ je navíc investorovi ztížena skutečností, že musí při zamýšlené investici do dluhopisu s možností předčasného svolání emise zevrubně prozkoumat parametry této události, zejména to pak znamená, že musí prozkoumat prospekt dluhopisové emise, kde by měly být podmínky a termíny takového předčasného svolání podrobně popsány. S odvoláním na minulé články připomenu, že svolání emise nebo její části je téměř vždy výhodné pro emitenta, protože je založeno na předpokladu, že se v budoucnosti mohou na trzích vyskytnout situace, kdy bude pro něj vhodné emisi „nakoupit zpět“ a získat nové finance vydáním nové emise, toto se pak stane v situaci, kdy jsou na trzích nižší výnosy, než je kupón svolávané emise, tedy než byly při jejím emitování. Emitenti tedy mohou vyměnit starší emisi s vyšším kupónem za novou emisi s nižším kupónem. Jakých „základních tvarů“ mohou nabývat tato předčasná svolávání emisí:
Svolání emise v určitém okamžiku v budoucnosti za danou cenu (Call Date)
Zkoumání dluhopisu MET z pohledu Call mohu zahájit v platformě svého brokera, kde mohu v popisu tohoto finančního nástroje vypozorovat upozornění na možnost svolání emise.
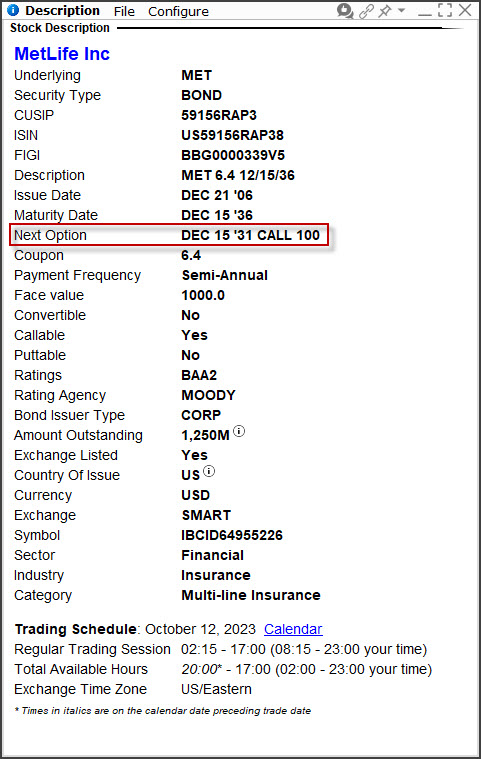
Přestože by mohlo toto zjištění Call data stačit, bude patrně vhodnější prozkoumat tuto okolnost detailněji v dokumentech týkajících se této emise. Prozkoumáním prospektu dluhopisu MET se splatností 15.12.2036 mohu zjistit, že emitent může provést níže uvedené transakce:

Pokud pořídím nyní dluhopis MET se splatností 15.12.2036, mohu zjistit, že emitent opravdu může svolat emisi nebo její část 15.12.2031 (1), tedy pět let před splatností tohoto dluhopisu. V odstavci se dále uvádí, že při svolání emise bude držitelům dluhopisů vydána hotovost v hodnotě „par redemption amount“. Mohu také zjistit, že celá emise nebo její část může být svolána kdykoliv před 15.12.1931 v případě, že nastane událost označená jako „tax event“ nebo „rating agency event“ (2). Mohu tak usoudit, že 15.12.2031 je tzv. First Call Date, pokud nenastanou ve společnosti MET Life události popisované jako „tax event“ a „rating agency event“, jejichž definice je dále v prospektu přesně popsána. Bude mě pak zajímat, co vlastně od emitenta obdržím, pokud bude emise svolána zpět, když toto plnění se v prospektu označuje za „par redemption amount“. V textu prospektu mohu zjistit následující:

V případě svolání obdržím opravdu Face Value mé investice (principal amount) plus úroky, které mi ke dni svolání náleží (myšleno úroky z následující kupónové výplaty, pokud je Call Date v termínu mezi výplatami kupónů). Mohlo by mě zajímat, jakým způsobem případné svolání emise zasáhne do výnosu nakoupeného dluhopisu, protože jeho pořízení bylo spojeno s očekáváním určitého výnosu a předčasné ukončení života mé investice svoláním se na plánovaném výnosu pravděpodobně projeví. Pomocí mého excelu mohu modelovat také tuto situaci podle obrázku níže:
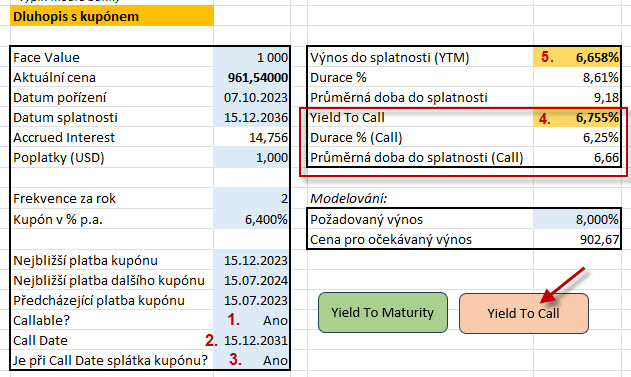
Kliknutí na tlačítko „Yield To Call“ mohu iniciovat výpočet výnosu do data svolání emise za podmínky, že mám vyplněny buňky „Callable?“ (1), „Call Date“ (2) a „Je při Call Date splátka kupónu?“ (3), vyplnění těchto buněk je z rozevíracích seznamů. Mohu potom pro daný dluhopis nechat skriptem vygenerovat pouze diskontované kupónové platby a splátku Face Value do Call Date a z nich stanovit výnos právě k tomuto datu – Yield To Call (4). Mohu pak po výpočtu konstatovat, že Yield To Call je ve výši 6.755% p.a., je tedy mírně vyšší než výnos do splatnosti (YTM), který je vypočten na úrovni 6.658% p.a. (5). Yield To Call je vždy mírně vyšší než YTM, protože je v něm promítnuta skutečnost, že obdržím splátku Face Value dříve, než bych na tuto skutečnost čekal do řádného termínu splatnosti dluhopisu a tato skutečnost mi umožňuje tyto dříve získané peníze dále zhodnocovat jinými způsoby. Přestože je toto poznání pro investora příjemné, je toto zjištění o vyšším výnosu mírně zavádějící. Emitent k předčasnému svolání emise totiž přikročí vždy pouze v případě, že to bude pro něj výhodné a to je v situaci, kdy svolávanou emisi nahradí novou emisí s nižším kupónem. Toto se pak stane za situace, kdy jsou na trzích nízké výnosy, to ale pro držitele dluhopisu znamená, že získané prostředky na trzích bude dále zhodnocovat s nižšími výnosy. Vyšší výnos vyplývající s Yield To Call tak trpí reinvestičním rizikem.
Svolání emise za cenu dle aktuální situace na trzích (Make-Whole Redemption)
Stanovené datum First Call Date a jasný výpočet ceny, kterou obdrží držitel dluhopisu může být nahrazena mírně složitější konstrukcí, která kombinuje výpočet „výkupného“ při svolání emise z aktuální ceny dluhopisu s přihlédnutím k aktuální situaci na dluhopisových trzích. Mohu tuto konstrukci demonstrovat na dluhopisu Walmart Inc. (WMT).

Společnost WMT emitovala dluhopis se splatností 8.7.2029, který nese kupón 3.25%m p.a., kupónové splátky jsou splatné vždy 8. ledna a 8. července každého roku do splatnosti, dluhopis mohu aktuálně pořídit za 916.67 USD. Pokud si zobrazím informace o nabízeném dluhopisu v mé obchodní platformě, mohu vypozorovat níže uvedené informace týkající se Call Date.
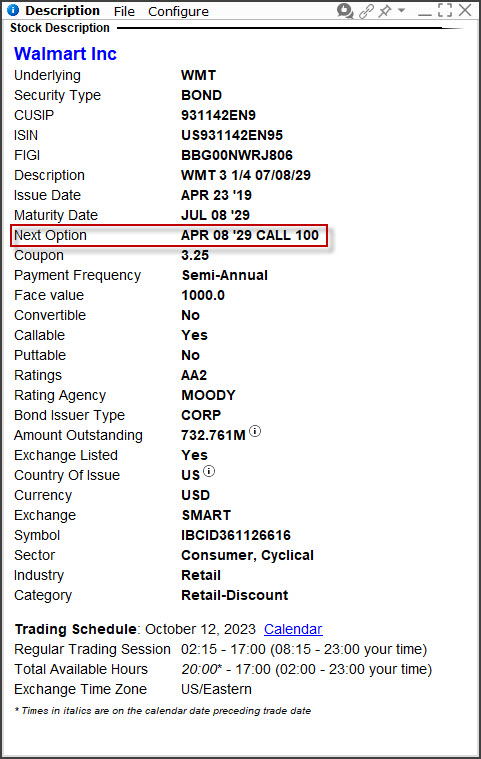
Ze zobrazeného vyplývá, že Call Date je stanoven na 8.4.2029, tedy tři měsíce před splatností dluhopisu. Pokud ale nahlédnu do prospektu dluhopisu WMT, je situace s předčasným svoláním jiná:

Žádné datum spojené se svoláním dluhopisové emise zde není stanoveno. V praxi to znamená, že emitent může dluhopisy svolat a vyplatit kdykoliv, kdy to bude pro něj výhodné, o tomto svém kroku informuje držitele dluhopisů oznámením v měsíčním předstihu. Mohu pak z prospektu vyčíst, že WMT emitoval v roce 2019 celkem tři emise dluhopisů s různými kupóny a s různou dobou do splatnosti (2.850%/2024, 3.050%/2026 a 3.25%/2029), analyzovaný dluhopis je pak variantou s nejdelší splatností v roce 2029 a kupónem 3.25% p.a.. Z textu v obrázku pak mohu vyčíst, že WMT může kdykoliv svolat emisi do 8.4.2029 za nějakých podmínek, datum 8.4.2029 z mé obchodní platformy tak není Call Date, ale den, od kterého už žádné svolání nehrozí, což je celkem významný faktický rozdíl.
Z textu dále vyplývá, že při svolání emise dostane držitel dluhopisu plnění, které je aktuálně vyšší hodnotou ze dvou nabízených variant: (1) obdrží Face Value a úrok, který naběhne držiteli dluhopisu z jeho kupónu ke dni svolání emise, den svolání emise se do výpočtu nezapočítává nebo (2) obdrží součet současné hodnoty všech „Remaining Sheduled Payments“ a opět úrok, který naběhne držiteli dluhopisu z jeho kupónu ke dni svolání emise. Při zjišťování současné hodnoty „Remaining Sheduled Payments“ svolavatel vypočítá jejich hodnotu diskontováních těchto budoucích plateb pomocí aktuálně obchodovaného výnosu amerického vládního dluhopisu se splatností jako je splatnost svolávaného dluhopisu, ke které přičte spread (v případě svolávané emise se splatností v roce 2029) ve výši +12.5 bazického bodu (+0.125%). Takto stanovenému výpočtu ceny dluhopisu k výplatě při svolání emise se říká „make-whole call provisions“.
Způsob výpočtu první varianty, tedy výplata Face Value a naběhlého úroku ke dni svolání je již asi jasná a je stejná, jako u předchozího příkladu s dluhopisem MET a pevně stanoveným Call Date. Druhá varianta je komplikovanější, nicméně není složité ji porozumět. Mohu si tak představit, že je na dnešní den (7.10.2023) ohlášeno předčasné svolání dluhopisu WMT se splatností v roce 2029 a s kupónem 3.25% p.a. Výpočet ceny dluhopisu k výplatě pak bude sestávat z několika kroků podle popisu v prospektu:
1/ Prvním krokem je stanovení všech budoucích plateb, které mi ke dni svolání emise (k dnešnímu dni) zbývají do splatnosti a které jsem očekával, že nastanou. Budou to tedy všechny pololetní kupónové platby a závěrečná splátka Face Value ke dni splatnosti, tedy k 8.7.2029. Tyto platby na obrázku níže:
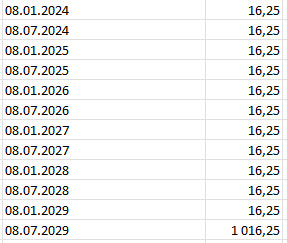
Dluhopis při kupónu 3.25% p.a. vyplácí 16.25 USD v pololetních termínech. Remaining Sheduled Payments je tak právě tato řada budoucího cash flow. Nyní bude zapotřebí, podle prospektu, získat jejich současnou hodnotu diskontováním každé této položky a provést jejich součet.
2/ Provést diskontování jednotlivých položek této řady plateb k dnešnímu dni není žádný problém, problémem je nalézt výnos, podle kterého budeme diskontovat. V prospektu je uvedeno, že výnos, kterým budeme diskontovat se bude rovnat aktuálnímu výnosu vládního dluhopisu s dobou splatnosti odkupovaného dluhopisu (8.7.2029) a k tomuto výnosu bude připočten spread ve výši 0.125%.

Hledání odpovídajícího vládního dluhopisu se splatností v červenci 2029 by mohl odpovídat dluhopis z obrázku výše, který má aktuální výnos ve výši 4.734% p.a. Pokud by byl vybrán k výpočtu tento dluhopis (způsob výběru a osoby, která jej vybírá, je v prospektu popsán) musel bych k tomuto výnosu přičíst definovaný spread (+0,125%), konečný výnos pro diskontování by tak činil (4.734% + 0.125%) konečných 4.859% p.a. Takto sečtený výnos pak bude použit pro sestavení součtu diskontovaných hodnot mých budoucích cash flow, tento výpočet pak mohu opět zařídit ve svém excelu.
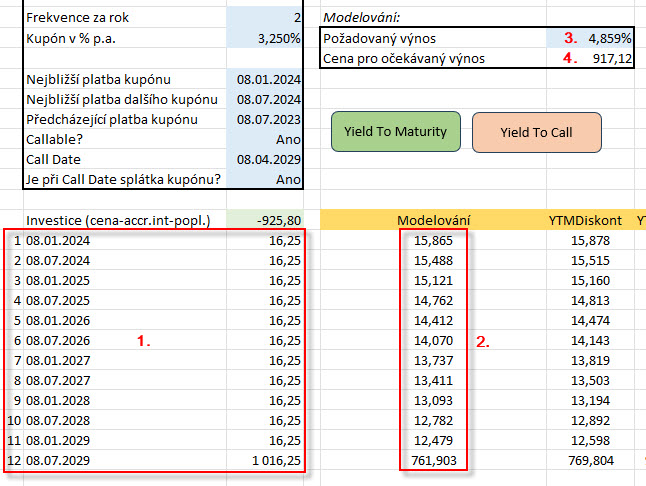
Jakýkoliv výpočet výnosu do splatnosti jakéhokoliv dluhopisu je hledání takového výnosu, který všechny budoucí peněžní toky z analyzovaného dluhopisu ve svém součtu diskontuje na aktuální cenu tohoto dluhopisu, musím tedy tyto toky nejdříve sestavit (1) a potom mohu hledat, jaký výnos mi tyto budoucí peněžní toky nadiskontuje do aktuální ceny. Mohu ale také tento výpočet obrátit a hledat pro požadovaný výnos odpovídající cenu dluhopisu, která jej pro danou řadu cash flow reprezentuje. Toto mohu pozorovat v diskontovaných cash flow ve sloupci „Modelování“ (2), kde jsou všechny peněžní toky diskontovány na současnou hodnotu výnosem 4.859% p.a. (3) (tento před výpočtem mohu do modře podbarvené buňky excelu na řádku „Požadovaný výnos“ zadat), což reprezentuje aktuální výnos vybraného vládního dluhopisu s přirážkou stanovenou v prospektu. Mohu pak vypozorovat, že tento součet pak dává číslo 917.12 USD (4), jako cenu, kterou bych mohl obdržet podle výpočtu v prospektu (v této ceně pak není ještě započítána drobná částka připadající na úrok z kupónu od dnešního dne do výplaty nejbližší kupónové platby). Pokud by tedy emitent přikročil nyní ke svolání emise, musel by držitelům dluhopisů vyplatit vyšší částku z hodnot a) hodnoty Face Value + úroku, který naběhne držiteli dluhopisu z jeho kupónu ke dni svolání emise – což je částka mírně vyšší než 1.000 USD, b) hodnoty 917.12 USD (s malou přirážkou za úrok do splatnosti nejbližšího kupónu). Obdržel bych tak plnění podle první možnosti a pokud by se mi podařili pořídit dluhopis za cenu nižší než je Face Value, obdržel bych na svolávaném dluhopisu zajímavý kapitálový výnos z rozdílu mezi touto pořizovací cenou a jeho výkupní cenou.
Sinking Fund
Vydání dluhopisu emitenta zavazuje k pravidelné výplatě kupónu a ke splátce Face Value u data splatnosti. Jedná se tak o „malé částky“ za života emise (kupónové platby) a velký výdaj u splatnosti dluhopisu (platba Face Value). Takový postup může emitentovi způsobit v budoucnosti (u splatnosti) značný nápor na jeho hotové peníze, a protože budoucnost nelze nijak zodpovědně předjímat, nemusí se s takovou záležitostí nakonec také úspěšně vypořádat. Na trh uváděnou emisi tak může emitent doprovodit vytvořením tzv. „Sinking Fund“, na který bude pravidelně odkládat prostředky ze své činnosti a z těchto prostředků pak bude v pravidelných intervalech skupovat zpět části vydané dluhopisové emise. Princip sinking fondu mohu demonstrovat na jednoduchém modelovém příkladu:
Společnost XYZ vydá desetileté dluhopisy za 100 milionů dolarů. Současně zřídí Sinking Fund, tedy jakýsi „Umořovací účet“, který nechá spravovat třetí stranou, na který se zaváže posílat každý rok trvání emise prostředky podle svých vlastních možností, například 10 milionů dolarů. V prospektu pak deklaruje, že po pěti letech života emise bude každý rok provádět Call ve výši 20% emise, na které využije prostředky se Sinking Fund. Pokud takto bude postupovat zbylých pět let do splatnosti dluhopisu, zbude mu na Maturity Date k vyplacení pouze 20% vydaných dluhopisů. Variant na strukturování příspěvků do Sinking Fund a možností časování využití takto nashromážděných prostředků je mnoho. Oddělení prostředků na svolávání části emisí pomocí takto zřízeného separátního účtu řízeného třetí osobou pak dává investorovi větší jistotu, že obdrží své prostředky vložené do dluhopisu zpět.
Napsat článek o dluhopisech tak, aby to byla zábava, je obtížné. Investování do cenných papírů s pevným výnosem není pravděpodobně tak dynamické, jak by si „akčně“ založený investor přál, nicméně může skrývat úskalí, která nejsou na první pohled patrná. Je tak jasné, že rozhodnutí vložit své prostředky do dluhových cenných papírů musí předcházet alespoň zevrubná analýza, která může odhalit případná úskalí takové investice. Rozhodovací procesy při nákupu takových cenných papírů by pak mělo doprovázet zamyšlení, jaké cíle svou investicí sleduji, co od ní očekávám a nakolik je pro mě vhodná. Doufám, že výše napsané řádky alespoň mírně přispěly k řešení některých myšlenkových procesů, spojených s dluhopisovým investováním.
Analytický excel popisovaný v tomto článku je k dispozici v diskuzním fóru ve vlákně k tomuto článku, obsahuje VBA skript, který lze volně kopírovat nebo upravovat podle vlastních potřeb.
Komentáře a příspěvky k tomuto článku prosím směrujte do Diskuzního fóra do tohoto vlákna :c)
Sleduj facebook, napiš e-mail nebo tweet