„Poznání nezabírá místo“ (La Casa De Papel, Berlin) byla narážkou na nutnost teoretické přípravy při vyloupení španělské státní tiskárny peněz a jako motto má nepochybně svůj vlastní půvab. Studium starších a poctivých knih o opčním tradingu, které jsou prošpikovány teoretickými úvahami spojenými s tradingem těchto derivátů může pomoci poodhalovat nejenom neviděné souvislosti, ale také dát odpovědi na nejjednodušší otázky nebo nacházet způsoby řešení věcí, které by mohly být nakonec prakticky využitelné. Listování pasážemi těchto publikací pak bylo inspirací k napsání těchto řádků.    

   Zabývat se Volatilitou by nemělo pro opčního obchodníka představovat ztrátu času. Přestože si to pravděpodobně začínající opční obchodník dostatečně neuvědomuje, je pozorování a pochopení principů volatility v souvislosti s chováním opčních kontraktů podstatou opčního tradingu. Mohu si myslet o jednotlivých přístupech, technikách a strategiích cokoliv, ale jednoduše vypozorovat, že vypisovat Short Call opce se ziskem +100 USD Prémia ve vzdálenosti 10% od současné ceny nebo 30% od současné ceny mi umožňuje jiná úroveň Implied Volatility zahrnutá do ceny vypisovaného opčního kontraktu, není nic nepochopitelného a světoborného s čím by se i opční začátečník nebyl schopný ztotožnit. Vyšší Volatilita představuje vyšší opční ceny je velmi jednoduchá souvislost, které patrně žádnému opčnímu traderovi nemohla uniknout.

   V článcích Volatilita a cenový pohyb – I.  a Volatilita a cenový pohyb – II. jsem se již zabýval některými aspekty Implied Volatility společně s praktickými způsoby, jak si její hodnoty mohu aplikovat na své obchody nebo alespoň na pozorování historických cenových dat, které bych pro své obchody mohl využít. V dnešním článku bych chtěl popustit uzdu teoretizování a úvahám nad základními problémy Volatility a cenami opčních kontraktů, skoro by se pak mohlo zdát, že jsem tento článek měl napsat jako první v pořadí této tříčlánkové minisérie.

   Jsem developerská společnost a stavím bytové komplexy. Vyřídit všechna povolení, nakoupit vhodné pozemky, zaplatit projektovou dokumentaci, řídit vlastní stavbu, nakupovat materiál a proplácet provedené stavební a související práce jsou náklady, které mohu velmi jednoduše sumarizovat do pravděpodobně velmi jednoduché excelovské tabulky. Ukončením projektu pak mohu jednoduše zjistit, že jsem na výstavbu deseti bytových jednotek utratil 10 milionů korun, a protože jsou všechny bytové jednotky stejné (pro jednoduchost), mé náklady na jednu bytovou jednotku činí jeden milion korun. Protože jsem se rozhodl prodávat jednotlivé jednotky na volném trhu, mé základní obchodní povědomí pak tvoří základní premisa, že hodnota jedné prodávané jednotky nesmí klesnout pod BreakEven bod mé transakce, tedy pod jeden milion korun. Spuštěním prodejní kampaně s cenou 1,000.000,- Kč za jeden byt mohu zjistit tržní reakce účastníků realitního trhu a vyhodnocovat, nakolik je moje nabídka realistická, jinými slovy, jaká je pravděpodobnost, že se vystavěných bytových jednotek zbavím alespoň za náklady výstavby. Pokud bude poptávka obrovská a nabídky na uzavření kupní smlouvy se jen pohrnou, bude to znamenat, že má nabídka je podhodnocena. V případě úrovně BreakEven ceny jeden milion korun, kterou jsem si vypočítal jako součet opravdu vynaložených nákladů, mohu o této cenové úrovni hovořit jako o Teoretické Ceně a mohu pak při pozorovaném převisu poptávky po mnou vystavěných bytech nad jejich nabídkou hovořit o skutečnosti, že z pohledu kupujících se má nabídka patrně pohybuje pod aktuální tržní cenou a Teoretická Cena představuje investici do podhodnoceného aktiva. Nebude patrně problémem na realitních serverech zjistit, že se obdobné byty prodávají za 1,500.000,- Kč a výše, takže nákup této nemovitosti bude představovat patrně dobrou investiční příležitost. Může ale naopak nastat opačná situace, kdy se realitní trh může dostat pod výrazný tlak způsobený nějakou externí ekonomickou událostí a má cenová jednomilionová nabídka se nesetká se zájmem investorů a zůstane nevyslyšena. Nezájem o tento typ investice si pak mohu jednoduše vysvětlit tak, že má Teoretická Cena je oproti aktuální tržní ceně značně nadhodnocena a tento typ investice pak bude pravděpodobně velmi rizikovou investicí s problematickou návratností.

   Ve skutečnosti by ale situace nebyla tak černobílá, potácející se mezi zájmem o všechno a nezájmem o nic, protože by ji pravděpodobně doprovázelo povědomí prodejce o aktuální úrovni cen na realitním trhu za současné alespoň obecné znalosti kupců o možných nákladech na výstavbu nabízených bytových jednotek. Mohl bych pak svůj příklad s výstavbou modifikovat do situace, kdy přidám k teoretické ceně bytové jednotky nějaký její další díly (například +500.000,- Kč, 700.000,- Kč…) a za cenu 1,500.000,- Kč, 1,700.000,- Kč… se je pokoušet prodat. Vzhledem k aktuální ceně na realitním trhu, která by této ceně mohla odpovídat, mohu pak celý problém „zmatematizovat“ na výpočet Očekávaného výnosu z mé developerské činnosti, když toto očekávání ohodnotím pravděpodobností, s jakou se mi podaří prodat vystavěné byty za předem stanovenou cenu. Mohu pak například předpokládat, že pět bytů (50%) prodám ihned za její nabízenou cenu 1,500.000,- Kč a toto bude představovat pravděpodobný profit (5 x 500.000,- Kč) ve výši 2,500.000,- Kč při nákladech 1,000.000,- Kč na jeden byt, tři byty (30%) prodám za částku 1,700.000,- Kč  a toto bude představovat pravděpodobný profit (3 x 700.000,- Kč) ve výši 2,100.000,- Kč a zbylé dva byty (20%) prodám za částku 1,800.000,- Kč a toto bude představovat pravděpodobný profit (2 x 800.000,- Kč) ve výši 1,600.000,- Kč. Sestavením výpočtu podle jednotlivých pravděpodobností pak mohu vypočítat: (50% x 2,500.000) + (30% x 2,100.000) + (20% x 1,600.000) = 1,250.000,- Kč + 630.000,- Kč + 320.000,- Kč = 2,200.000,- Kč. Můj očekávaný výnos pak bude právě tato suma.

   V jednoduchém příkladu pak mohu vypozorovat čtyři důležité faktory, když tři z nich vygenerovaly nějakou konkrétní očekávanou hodnotu a které samy o sobě nesou stigma mírné neurčitosti – Očekávaný výnos, Pravděpodobnost a samotný Výpočet. Je asi zcela jasné, že Očekávaný výnos může mít různou velikost, protože je bezprostředně určen stanovením Pravděpodobnosti možností, které mohou v mém počínání nastat, a nakonec Výpočet nemusím provádět pouhým zvážením jednotlivých pravděpodobností, ale mohu nasadit více či méně sofistikované výpočetní modely, které si s výpočtem mohou lépe poradit. Čtvrtým faktorem vstupujícím do těchto úvah je pak Teoretická Cena, která je vypočtena přesnou kalkulací přesných čísel (v mém příkladu součet všech nákladů souvisejících se stavbou bytů).  

Očekávaný výnos

   Provedení ojedinělého obchodu nebude patrně vyžadovat nijak astrální traderské úvahy o tom, jak a za jakých podmínek se takový obchodní pokus realizuje. Pokud však chci svému obchodování vtisknout podobu systematičnosti a pragmatičnosti, nemohu se ubránit alespoň základnímu a obecnému nadhledu nad svým obchodním konáním. K následujícím řádkům si vypůjčím příměr, který popisuje téměř každá tradingová publikace nebo kniha o základech statistiky a pokusím se jej aplikovat na můj ukázkový příklad s bytovou problematikou, který si pro tuto ukázku upravím. Mých vybudovaných deset bytů pak nebude stát stejně, protože budou nestejně velké a jejich hodnota bude taková, že byt číslo jedna bude mít hodnotu jeden milion korun, byt číslo dvě bude oceněn na dva miliony korun, za byt číslo tři budu požadovat tři miliony korun atd. …až nakonec byt číslo deset bude mít cenu deset milionů korun. Budu předpokládat, že budu mít značné množství investorů, kteří budou ochotni zaplatit za každý nabízený byt mnou určenou částku a deset z nich si pak sezvu v jeden den na jedno místo a učiním jednoduchý pokus přidělení nabízeného bytu náhodně vybranému investorovi na základě náhodného výběru. Zařídím to jednoduše, do připraveného kyblíku vhodím deset míčků, každý s označením ceny jednoho bytu, budu mít tedy připraven jednomilionový až desetimilionový míček. Každý z těchto deseti investorů pak bude mít možnost vytáhnout jeden míček a bude mít povinnost mi zaplatit určenou cenu za míčkem reprezentovaný byt. Co mohu od každého takového pokusu očekávat, tedy kolik průměrně obdržím za každý takový pokus? Součet všech cen míčku v kyblíku je (1 milion +2 miliony +3 miliony +…+10 milionů) = 55 milionů, při deseti míčcích mohu očekávat, že průměrně budu moci očekávat příjem za každé vytažení míčku (55 milionů/10) částku 5.5 milionů korun, toto je můj průměrný Očekávaný výnos z každého jednotlivého pokusu. Při deseti vytaženích míčků bych tak v součtu dostal očekávanou cenu, kterou jsem nakonec také požadoval, to je velmi jednoduchá matematická úvaha, která nepotřebuje žádný další komentář. Mohu však tuto úvahu rozšířit do teoretické roviny, kdy budu moci předpokládat, že budu mít neomezené množství pokusů vytáhnout míček z kyblíku, zapsat si jeho cenu a vrátit jej zpět k dalšímu možnému vytažení spolu se zbylými míčky. Mohu pak zorganizovat soutěž, kdy po investorech budu požadovat, aby mi zaplatili za možnost každého vytažení míčku nějakou určenou částku. Na základě znalostí o počtu míčků v kyblíku, jejich jednotlivé ceně a nahodilosti výběru, mohu pak označit investory, kteří mi nabízejí za svůj pokus částku nižší než je 5,5 milionů korun, jako jedince, kteří mi nabídli menší než Teoretickou Cenu a kteří si vytvořili velmi dobrý předpoklad pro to, aby mohli na svých pokusech profitovat. Při nekonečném množství pokusů vytahování a vracení zpět by pak měli jistotu, že rozdíl mezi částkou 5.5 milionů korun a jimi nabízenou nižší cenou je jejich profit, tedy Očekávaný výnos. Systematické pořizování pod Teoretickou Cenou by pak mělo vést k Očekávanému výnosu, by mohla být velmi zjednodušená formule, kterou netřeba opět nijak dramaticky komentovat, nicméně je to jenom teorie. V takovém ideálním světě by pak sumarizace všech nekonečně mnoha pokusů vedla ke zjištění, že částka 5.5 milionů korun je střední hodnota (mean) a výsledky ostatních pokusů by pak byly rozptýleny s nějakou pravděpodobností kolem této střední hodnoty, ve výsledku bych pak mohl zjistit, že zjištěné hodnoty mají Normální rozdělení a mohu na ně aplikovat pravidlo „tří sigma“, tedy zjištění, s jakou pravděpodobností se jednotlivé výsledky nacházejí vzhledem ke střední hodnotě, tyto úvahy jsem pak podrobněji rozebral v článcích Volatilita a cenový pohyb – I.  a Volatilita a cenový pohyb – II.  a není tak zapotřebí tyto základy opakovat.         

   Ve skutečnosti však s byty neobchoduji a nemám žádný pomyslný kyblík s míčky, nekonečně pokusů a nekonečně mnoho investorů. Jsem opční obchodník a s myšlenkou nakupování za méně než Teoretickou cenu s výpočtem Očekávaného výnosu si tak mohu pouze teoreticky pohrávat na bázi matematických operací a jejich interpretací a na toto bych se pokusil zcela obecně zaměřit. Teoretická cena a Očekávaný výnos jsou propojené hodnoty, protože v základní logice každého obchodu by pro mě mělo být výhodné zjistit alespoň přibližně teoretickou cenu, která se bude promítat do očekávaného výnosu, čím lépe do obchodu vstoupím, tím lepší očekávaný výnos mohu požadovat. Velmi jednoduchý „obchodní axiom“, jeho podstatu je však nemožné racionálně naplnit, protože zjistit, co je skutečně dobrá vstupní cena (Teoretická Cena) je nemožné, je totiž zcela závislá na subjektivních pohledech účastníka obchodu, a je nakonec i jedno, jestli si tento parametr nastaví podle svého vlastního názoru a rozhodnutí nebo jej vtělí do vytvořeného algoritmu nějakého automatizovaného systému. Pokud bych se pokusil o modelování Očekávaného výnosu náhodně vybraného opčního obchodu, mohl bych vyjít s nejjednodušší představy o Teoretické ceně, kterou bych vtiskl do následující úvahy. Na obrázku níže je opční řetězec akcie GS (Goldman Sachs) s expirací za 30 kalendářních dnů. Z obrázku vyplývá, že se akcie GS aktuálně pohybuje kolem ceny 180 USD a já bych chtěl pořídit například Long Call na strike 180. Za kolik bych ji měl pořídit, abych zjistil, jaká je její Teoretická cena a jaký by měl být Očekávaný výnos, pokud nemám žádné povědomí o matematickém modelování?

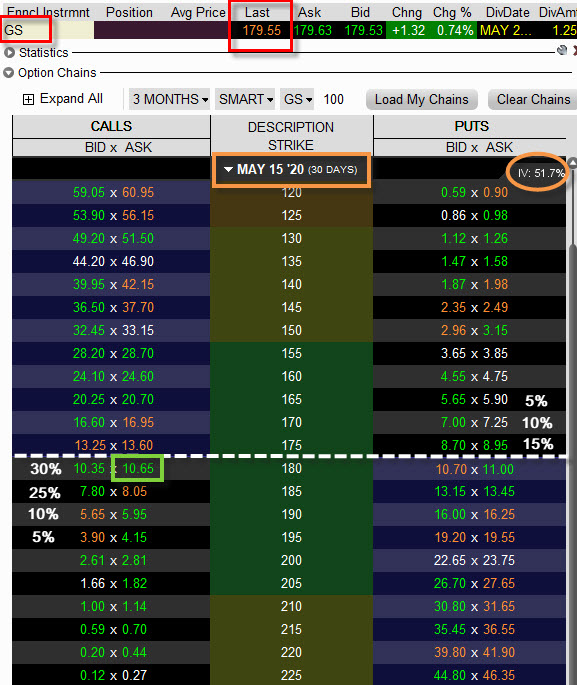
   Zelený obdélník představuje uvažovanou GS Long Call 180 pozici k pořízení. Její cena je nyní -1.065 USD a má základní otázka nyní zní – je to dobrá cena? Je velmi obtížné na první pohled zjistit, zda je toto dobrá nebo špatná cena, jestli se pohybuje pod/nad nějakou Teoretickou cenou a jestli je její nákup pro mě nakonec výhodný. Mohu ale takovou úvahu poměřit s Očekávaným výnosem takové investice a zjistit, nakolik je výdej peněz na tento nákup pro mě efektivní. Stanovit hodnotu takového výnosu musím, chtě nechtě, spojit se stanovením pravděpodobnosti, s jakou mohu očekávat určitý výnos. Jsem optimista a věřím, že cena akcie GS bude spíše růst než aby klesala, proto jsem podle obrázku přiřadil jednotlivým strike pravděpodobnost jejího dosažení vyjádřenou v procentech. Mohu tak zcela konkrétně vypozorovat, že při expiraci Long Call 180 předpokládám, že na 30% bude cena akcie GS stejná, jako při vstupu do obchodu, tedy přibližně 180 USD. S 25% pravděpodobností pak počítám, že cenu u expirace bude 185 USD a méně pravděpodobné (10%) pak bude dosažení ceny 190 USD. 5% pravděpodobnost pak přiřazuji možnost dosažení ceny 195 USD. Podobná očekávání pak mohu vyznačit také pro případný pokles ceny akcie GS do expirace, s 15% pravděpodobností předpokládám pokles na cenu 175 USD, 10% pravděpodobnost přiřazuji cenovému poklesu na hranici 170 USD a s 5% pravděpodobností očekávám pokles na úroveň 165 USD. Takto různě stanovené pravděpodobnosti pak budou pro mou jednoduchou opční GS Long Call 180 pozici znamenat různě stanovené Očekávané výnosy. Pokud cena poroste na hodnotu 185 USD, bude to znamenat, že má Long Call 180 bude mít při expiraci hodnotu +5 bodů (+500 USD) – této možnosti jsem přiřadil pravděpodobnost 25%. V případě, že cena naroste do expirace na hodnotu 190 USD, má Long Call 180 bude mít hodnotu +10 bodů (+1.000) USD a této možnosti přiřazuji pravděpodobnost 10%, významnému uptrendu na úroveň 195 USD do expirace pak dávám šanci z 5% a znamenalo by to, že má Long Call 180 bude mít hodnou +15 bodů (+1.500 USD). V opačném případě stagnace a poklesu ceny akcie GS to pak bude znamenat, že v případě, že cena zůstane na hodnotě 180 USD, klesne na 175 USD, klesne níže na 170 USD nebo se propadne na 165 USD – bude má Long Call opce bezcenná a očekávaný výnos bude nulový, těmto možnostem jsem pak přiřadil výše popsané pravděpodobnosti (180 USD/30%, 175 USD/15%/ 170 USD/10% a 165 USD/5%). Protože jiné možnosti nepřipouštím, je součet všech pravděpodobností 100%. Co tedy mohu očekávat? V jednoduchém výpočtu přiřazení jednotlivých výnosů při stanovených pravděpodobnostech jejich očekávání zjišťuji:

(1.500 USD*5%) + (1.000 USD*10%) + (500 USD*25%) + (0 USD*30%) + (0 USD*15%) + (0 USD*10%) + (0 USD*5%) = 75 USD + 100 USD +125 USD + 0 USD + 0 USD+ 0 USD+ 0 USD = +300 USD

   Při nabízené ceně 1.065 USD za GS Long Call 180 z burzovní platformy mého brokera se zdá mnou vypočítaná cena 300 USD několikanásobně nižší. Co je špatně? Můj broker mi nabízí značně přemrštěnou cenu nebo jsou má očekávání zcela mimo realitu? Jedno nebo druhé, ale také obojí současně, aniž bych si to totiž uvědomil, vytvořil jsem jednoduchý matematický model ocenění mého uvažovaného opčního GS Long Call 180 opčního kontraktu a poměřil ho s obchodní realitou. Zcela jistě se jeho výstup – vypočítaná Teoretická nákupní cena neshoduje s aktuální tržní situací a mohl bych pak svůj postup řešení hledání vhodné Teoretické ceny rozdělit na dva základní problémy. Zvolil jsem špatný matematický model nebo jsem do správného matematického modelu vložil nesprávná data nebo také mohou obě možnosti současně být špatně?

   Přestože jsem vytvořil velmi primitivní výpočetní metodu, mohu si být zcela jistý, že jakákoliv jiná a sofistikovanější metoda výpočtu ceny opce bude vždy záviset na nějakém předpokladu a očekáváních, která v budoucnosti nastanou a tuto budoucnost tyto metody také nějakým specifickým způsobem oceňují. Trvalá přítomnost nejistoty pak odebírá těmto výpočetním metodám, reprezentovaných více či méně dokonalými matematickými modely, stigma absolutní dokonalosti, a to je pravděpodobně to, co dělá trading tak neuvěřitelně zajímavým a pozoruhodným. Pokud bych připustil ve své fantazii existenci absolutně dokonalých a efektivních trhů, nemohl bych pak na takto dokonalých trzích vůbec fungovat, protože by všechna budoucí očekávání již byla do cen investičních nástrojů (opcí nevyjímaje) beze zbytku započtena na základě absolutně dokonalých cenových modelů. Mé fungování na trzích pak vychází z jednoduchého předpokladu, že mé budoucí očekávání je jiné, než je očekávání celých trhů a z těchto rozdílů pak mohu poskládat filozofii mého obchodního přístupu.  

   Své očekávání pohybu cen akcie GS do doby expirace opčního kontraktu GS Long Call 180 jsem samozřejmě zvolil „od pasu“ a nemá to nic společného se skutečností, s kterou bych se mohl ztotožnit. Mnou stanovené pravděpodobnosti počítaly pouze s velmi omezeným scénářem stanovení její výše při dosažení určitých kulatých hodnot reprezentovaných jednotlivými strike pod a nad současnou cenou a neřešily situace, kdyby cena zakončila na zcela jiné ceně a také jsem své očekávání vměstnal pouze do možnosti pohybu +/-15 USD od současné ceny, větším pohybům jsem pak nepřidělil pravděpodobnost žádnou – fatální pokles nebo euforický nárůst jednoduše nepatřil do mého scénáře. Toto jsou první a zjevné nedostatky mého ocenění, které vyústily ve značně rozporuplný výpočet férové ceny mé zamýšlené investice. Navíc jsem více pravděpodobnosti „přihodil“ na stranu možného růstu ceny titulu GS než jsem vyhodnotil možnost, že cena akcie GS může do expirace mé opce také klesnout. Jak tedy mohu takovou pravděpodobnost více přizpůsobit náhledu účastníků trhů, více ji rozdrobit do jednotlivých možnosti cenových pohybů a vyvarovat se nesymetrickému očekávání možností růstů vůči poklesům?       

Rozdělení, Implied Volatilita a pravděpodobnost (zase…:c)

   V článku Je opce levná nebo drahá? jsem se pokoušel zjistit, jestli je aktuální nabídka cen opčních kontraktů vysoká nebo nízká a v článku Volatilita a cenový pohyb – II. jsem se zabýval mimo jiné otázkou, jaké predikce budoucího cenového pohybu mohu rozluštit z hodnoty Implied Volatility zjištěné z obchodní platformy nebo odvozené z ceny opčního kontraktu. Protože si mohu hodnotu aktuální Implied Volatility vyložit zejména jako pravděpodobnost očekávaného pohybu, pokusím se toto ještě dále rozvést do praktičtějšího pohledu na cenu opčního kontraktu, na jeho férovou cenu a na celkové očekávání výnosu z případného opčního obchodu. Můj výše vyznačený procentní odhad pravděpodobnosti dosažení strike ceny akcie GS byl patrně velmi neobratný a ve výsledku zpracovaném mým „opčním cenovým modelem“ nabídl zcela nesmyslnou částku jako hodnotu pořizované opce se strike „na penězích“. V obrázku s opčním řetězcem akcie GS mohu v pravém horním rohu zjistit, s jakou přibližnou hodnotu Implied Volatility pracovala obchodní platforma při zobrazených cenách opčních kontraktů, které mohu na obrázku vypozorovat. Protože je stanovení této hodnoty Implied Volatility proprietární záležitostí a není možné se dozvědět, jakým způsobem je tato hodnota vypočtena a dokonce co vlastně přesně znamená, mohu z její hodnoty odtušit pouze základní očekávání trhů v budoucnosti. Drtivá většina obchodního software používá tuto hodnotu pro demonstraci přesvědčení, jaká je Implied Volatilita samotného podkladu a je odvozována z cenového ohodnocení opčních kontraktů na ATM strike a v jeho těsné blízkosti, a protože do těchto výpočtů nevidím, mohu s rozmrzelostí pozorovat, že se liší (nepatrně, ale liší) u každého jednotlivého brokera. Číslo, které reprezentuje takovou Implied Volatilitu v mém konkrétním případě akcie GS pro opční kontrakty s expirací za 30 kalendářních dnů je v mé obchodí platformě na úrovni 51.70%.   

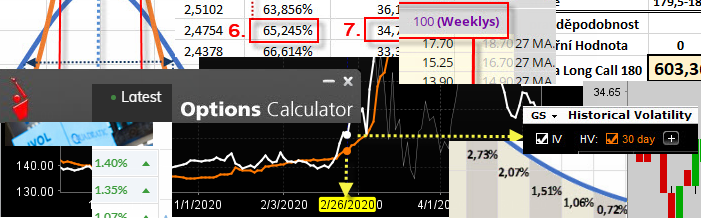
  Z četby mého webu mohu nyní jednoduše odvodit, že číslo 51.70%, jako hodnota Implied Volatility, znamená, že s pravděpodobností náležející první standardní odchylce (68.20%) se za rok bude cena akcie GS nacházet mezi hodnotou představující +/- 51.70% současné ceny akcie GS (179.55 USD). Předpokladem tohoto tvrzení je skutečnost, že se cenové pohyby akcie GS budou uskutečňovat zcela náhodně a tyto pohyby pak budou mít charakter Brownova pohybu (…úplně živě nyní vidím našeho tělnatého fyzikáře, jak vhodil do kádinky s vodou zrnka hypermanganu, které klesaly ke dnu zanechávajíce za sebou načervenalé chaotické stopy trasy, kterou si klestily ke dnu nádoby se slovy „tak toto je mojí milí demonstrace Brownova pohybu“…). Náhodnost pohybu padajících zrnek a nevyzpytatelnost jejich pohybu je pak vlastní pozorování, jehož naměřené hodnoty by mohlo mít Normální Rozdělení. Pokud připustím tento předpoklad, mohu se věnovat jednotlivým pravděpodobnostem podle tohoto rozdělení a toto aplikovat na moje velmi zjednodušené modelování ceny GS Long Call 180 opce na ATM strike. Prvním zádrhelem je ale skutečnost, že mě nebude zajímat, kde se bude s nějakou pravděpodobností nalézat cena akcie GS za rok, ale jakou by mohla mít cenu při expiraci mého opčního kontraktu, tedy za jeden měsíc. V článku Volatilita a cenový pohyb – I. jsem popisoval způsob, jakým lze převádět hodnotu Implied Volatility z jejího ročního tvaru na jednodenní bázi pomocí odmocniny času. Za předpokladu, že kalendářní rok má 252 obchodních dnů, mohu získat denní hodnotu Implied Volatility vydělením roční Implied Volatility druhou odmocninou z čísla 252. Pokud tedy pozorovatelná hodnota Implied Volatility GS je na úrovni 51.70%, mohu prostým vydělením zjistit, že 51.70%/15.87 = 3.25%. Tuto jednodenní Implied Volatilitu pak mohu aplikovat na různě dlouhé časové periody do budoucnosti a extrapolovat pravděpodobnosti, s jakou mohou nastávat možné cenové pohyby. Takové „pravděpodobnostní prognózy“ pak vypočítám jako hodnoty denní Implied Volatility (3.25% v mém případě) vynásobené druhou odmocninou času, za který chci tyto pravděpodobnosti získávat. Má sledovaná GS Long Call 180 opce má expiraci za měsíc (30 kalendářních dnů), proto mě bude zajímat, jaká bude pravděpodobnost pohybu podle Implied Volatility právě za těchto třicet dnů, tedy při expiraci mé nakoupené GS Long Call 180 opce, této pak přísluší expirace k 15.5.2020. Obrázek jsem pořídil 15.4.2020, spočítám si tak, kolik obchodních dnů toto bude představovat do expirace 15.5.2020, konkrétně pak tomuto období přísluší čtyři víkendy, takže obchodních dnů bude 22. Mohu proto jednodenní Implied Volatilitu 3.25% vynásobit druhou odmocninou z 22, abych zjistil (3.25%*4.69), že získávám měsíční Implied Volatilitu na úrovni 15.24 %. Mohu tak toto číslo interpretovat jako 68% pravděpodobnost (první standardní odchylka), že za měsíc se bude cena akci GS pohybovat na úrovních +/- 15.24% aktuální hodnoty. Toto odvození jednodenní Implied Volatility a její převod na jiné časové úseky má svou logiku, nemohu se však ubránit pocitu, že toto číslo měsíční Implied Volatility je „vytrženo z kontextu“. Hodnota roční Implied Volatility 51.70% počítá s 365 dny v roce, 52 týdny představující 104 dnů, kdy se neobchoduje a s 9 dny svátků, které představují Exchange Holidays (dny, kdy se na burze neobchoduje), proto je celkové roční číslo (365 – 104 – 9) obchodních dnů 252, má počítaná měsíční perioda ale například žádné svátky neobsahuje, takže může docházet k mírnému zkreslení vypočtené měsíční Implied Volatility. Tuto konstrukci mohu nahradit jiným přístupem k výpočtu, a to počítáním budoucí pravděpodobnosti pohybu v nějakém časovém rámci zvolením počtu period, představující počet opakování této sledované periody v období jednoho roku. Pokud tedy pozoruji a chci vypočítat měsíční Implied Volatilitu, zjišťuji, že měsíční perioda se opakuje v v jednom kalendářní roce 12x bez ohledu na délku měsíce, počet dnů víkendů a svátků, mohu pak vydělit roční Implied Volatilitu 51.70% druhou odmocninou čísla 12 (počet opakování periody za rok) a obdržet měsíční Implied Volatilitu za takto se opakující periodu (51.70%/3.46), která činí 14.94%. Rozdíl je oproti předchozímu výpočtu o 0.30 procentního bodu odlišný a při ceně akcie GS na 179.55 USD to činí něco málo přes půl dolaru. Připadá mi, že tento výpočet je k pravděpodobnosti spravedlivější, než vytržený konkrétní měsíc (bez svátků) jako v příkladu výše.

   Vypočítaná hodnota +/-14.94% tak jednoduše znamená, že do expirace mohu s pravděpodobností 68.20% očekávat, že se cena bude pohybovat v intervalu +/-14.94% od aktuální ceny akcie GS na aktuální úrovni 179.50, což v absolutním vyjádření znamená, že cenový pohyb s touto pravděpodobností činí +/- 26.79 USD, v dolarovém vyjádření pak mohu konstatovat, že existuje 68% pravděpodobnost, že se cena akcie GS za měsíc bude nacházet v oblasti 152.71 USD – 206.29 USD. V jiné oblíbené interpretaci stejného zjištění pak mohu také se stejnou vážností předpokládat, že v 68% procentech času do expirace se bude cena akcie GS pohybovat v tomto cenovém rozpětí. Toto vše již na tomto webu bylo popsáno a není to nic závratného. Grafické vyobrazení této pravděpodobnosti je na obrázku.

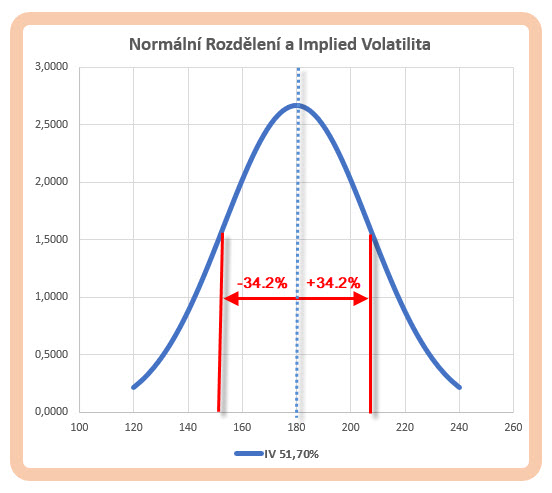
   Vysoká roční Implied Volatilita na úrovni 51.70% a 14.94% přepočtených na měsíční bázi je dosti vysoká a dává tak pravděpodobnosti 68.20% celkem široký prostor k pohybům. Gaussova zvonovitá křivka je tak výrazně zploštělá a mám ji vynesenu na cenové ose 120 USD až 240 USD možného měsíčního pohybu akcie GS. Vlastnostmi těchto křivek a jejich srovnáním jsem se zabýval v článku Volatilita a cenový pohyb – II., v detailech se nyní k tomu již vracet nebudu. Je tak patrné, že výpočet měsíční Implied Volatility dělením její roční hodnoty odmocninou z dvanácti (tedy konstantou) bude znamenat, že pokud se hodnota roční Implied Volatility bude snižovat, bude se snižovat cenový rozsah se stejně vypočítanou pravděpodobností, například 68.20% náležející první směrodatné odchylce. Na obrázku níže je pak stejná situace na akcii GS, ale hnědou Gaussovou křivkou je vykresleno rozložení s měsíční Implied Volatilitou na úrovni pouze 30%.

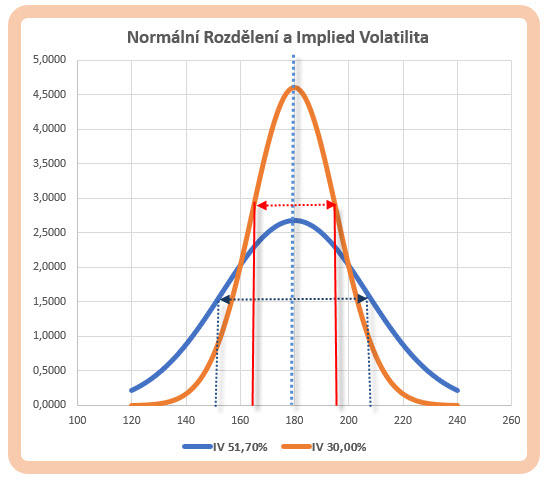
   Křivka je výrazně špičatější a vyšší a znamená, že s větší pravděpodobností se budou cenové pohyby rozprostírat kolem aktuální ceny (střední hodnoty) na úrovni 179.55 USD než v případě stejného předpokladu s vyšší Implied Volatilitou. Pohyb reprezentovaný pravděpodobností 68.20% vyznačený červeně je tak ve výrazně užším pásmu a představuje měsíční pohyb +/- 15.55 USD.

   Pokud jsem tedy schopen vypočítat, že s pravděpodobností 68.20% se uskuteční měsíční pohyb akcie GS při Implied Volatilitě 51.70% o velikosti +/-14.94%, a že to v dolarovém vyjádření představuje +/- 26.79 USD, nebude patrně problém tento výpočet aplikovat na jakoukoliv jinou vzdálenost od aktuální ceny v měsíčním horizontu a této vzdálenosti také přiřadit odpovídající pravděpodobnost (podotýkám za předpokladu existence Normálního Rozdělení pohybu ceny akcie GS). Budu potom moci aplikovat tyto výpočty na zjištění férové ceny mnou zkoumaného GS Long Call 180 opčního kontraktu, kde mě budou zajímat hledané pravděpodobnosti dosažení určitých cenových úrovní (například hodnoty strike „mimo peníze“) a tyto dosadit do mého velmi primitivního cenového modelu.

   K nalezení takových údajů (měsíční pravděpodobnost hledaného pohybu) mi ovšem neposlouží obyčejná trojčlenka, ale musím si takovou hodnotu zjistit mírně sofistikovanějším přístupem, který je zabudovaný (naštěstí) do Excelu. Jednotlivé pravděpodobnosti jednotlivých výskytů u Normálního rozdělení totiž „neleží na přímce“, ale jejich hodnoty tvoří křivku, jejíž tvar se budu pokoušet nalézt a z těchto bodů na křivce pak budu moci odezírat jednotlivé pravděpodobnosti pro jednotlivé pohyby. Takovou křivku vykresluje Kumulativní Distribuční Funkce a jednotlivé body na této křivce znamenají pravděpodobnost, že nějaká náhodná hodnota (pohyb akcie GS v horizontu jeden měsíc) bude menší než hodnota, kterou aktuálně chci výpočtem získat. Zní to podivně, ale interpretace je jednoduchá, jak vyplyne z dalšího textu. Jednotlivé hodnoty kumulativní distribuční funkce zjistím v Excelu pomocí předdefinovaného vzorce výpočtu =NORM.DIST. Tento ke svému výpočtu pravděpodobnosti, že náhodné budoucí pohyby budou mít pravděpodobnost menší než pro hledanou cenovou úroveň, potřebuje dva základní vstupní údaje popisující Normální Rozdělení, a tím je hodnota Střední Hodnoty (meanu) a hodnotu Standardní Odchylky, o výpočet se pak Excel postará sám. Za střední hodnotu mohu považovat současnou cenu akcie GS (179.55 USD) a hodnotu standardní odchylky pak mám určenou hodnotou Implied Volatility (převedenou na měsíční bázi). Na obrázku níže je pak obrázek excelovského sešitu, kterým jsem hledal odpovídající hodnoty kumulativní distribuční funkce.

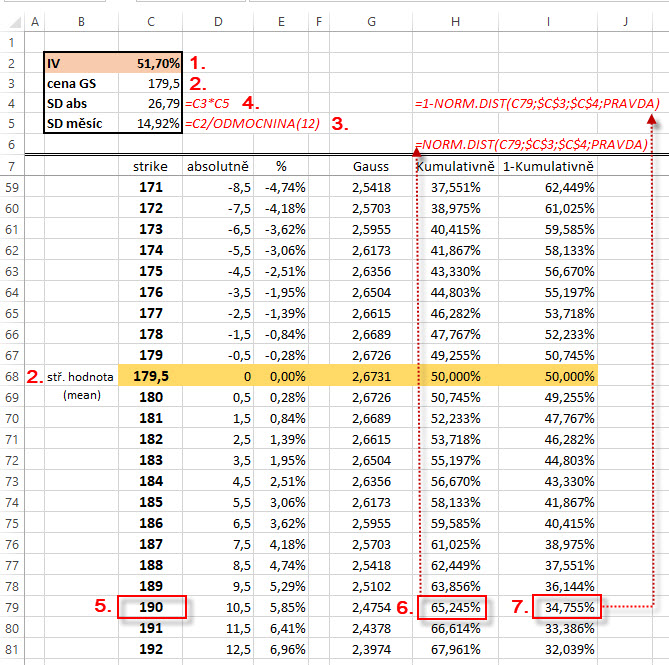
   V excelovském sešitu mám pro výpočet zadánu hodnotu Implied Volatility, kterou mohu odezírat ze své obchodní platformy, když v den provádění výpočtu byla hodnota Implied Volatility ve svém ročním tvaru na úrovni 51.70% (1). Střední hodnota Normálního Rozdělení, tedy výskytu budoucích hodnot bude aktuální cena akcie GS, která je na hodnotě 179.50 USD (2), kolem této hodnoty mě pak bude zajímat způsob rozptýlení budoucích hodnot, protože při této ceně chci investovat své peníze  do opčního kontraktu. Převod roční Implied Volatility na měsíční bázi provedu vydělením hodnoty roční Implied Volatility odmocninou čísla 12, která činí 14.92% (3). Zjištěnou měsíční Implied Volatilitu převedu na hodnotu dolarového pohybu podle aktuální ceny akcie GS, tato hodnota je 26.79 USD a představuje +/- měsíční pohyb ceny s pravděpodobností 68.20% první standardní odchylky (4).

   Pro pravděpodobnost měsíčního pohybu ceny GS z aktuální ceny 179.50 USD do oblasti 190 (5) provedu výpočet =NORM.DIST (hledaná hodnota; střední hodnota; standardní odchylka; PRAVDA), tedy v konkrétním tvaru =NORM.DIST(190; 179.50, 26.79; PRAVDA). Výsledkem je hodnota 65.245% (6). Ve vedlejším sloupci jsem provedl výpočet, který mi dopočítal kolik chybí zjištěnému procentu ve vedlejším sloupci do 100%, proto je jeho hodnota 34.755% (7). Co se mi vlastně pro hodnotu strike 190 s vypočítaným procentem 65.245% zobrazilo?

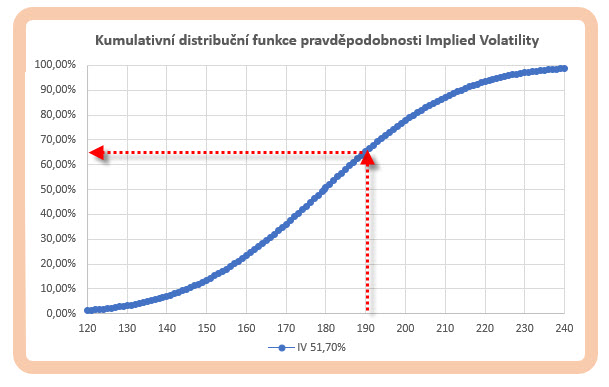
   Vygenerováním všech hodnot pro strike možných opčních kontraktů s hodnotami od 120 do 240 pro zobrazení křivky kumulativní distribuční funkce mohu vynést do grafické podoby a zjistit, že jednotlivé pravděpodobnosti opravdu nejsou v lineárním vztahu a křivka disponuje zakřivením, což se ostatně dá očekávat. Hodnota pravděpodobnosti 65.245% mi pak sděluje, že právě s touto pravděpodobností mohu očekávat u náhodných pohybů jejich rozsah do této hodnoty (190 USD) v horizontu jednoho měsíce. Se zbylou pravděpodobností (vypočtenou ve sloupci (7) excelovského sešitu) pak mohu předpokládat opak, tedy že hodnota bude za jeden měsíc vyšší než je 190 USD s pravděpodobností 34.755%. Na Gaussově křivce pak mohu pro tuto Implied Volatilitu pravděpodobnost pohybů v časovém úseku jeden měsíc graficky rozložit jako na obrázku níže.

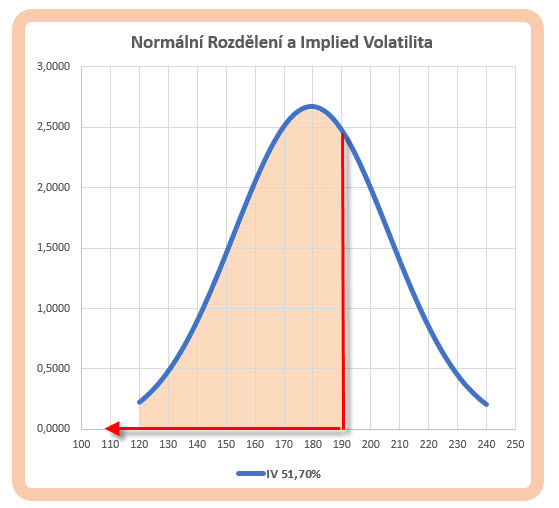
   Značně rozlehlejší oblast pohybů s větší pravděpodobností 65.245% reprezentuje možnost, že cena akcie GS ze současné ceny 179.50 USD bude klesat, stagnovat nebo růst do ceny 190 USD, naopak menší pravděpodobnosti 34.755% je pak přidělena možnost ceny akcie GS vystoupat na cenu 190 USD a vyšší. Toto vše při Implied Volatilitě na roční úrovni z mé platformy ve výši 51.70%. Mohu si s kumulativní distribuční funkcí samozřejmě také zaexperimentovat a mohu si ji nechat zobrazit při jiné výši Implied Volatility a pokoušet se přečíst její hodnoty a zobrazit její křivku, toto jsem vyzkoušel pro srovnání s roční Implied Volatilitou na úrovni 30%. Výsledek je na obrázku níže.

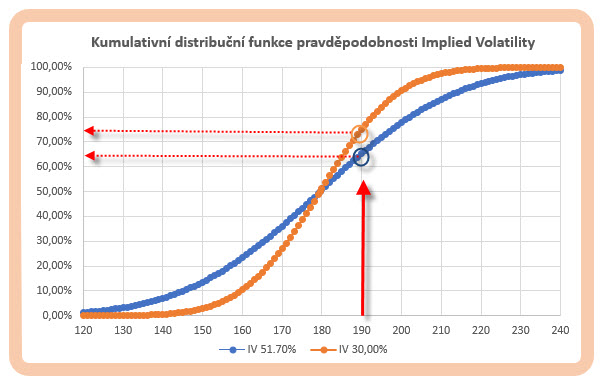
   Křivka nižší hodnoty roční Implied Volatility ve výši 30% a převedené na měsíční očekávané pohyby má výrazněji strmější průběh, který ostatně odpovídá také užší a ostřejší Gaussově křivce v textu výše. Nahuštění kolem střední hodnoty se tak projevuje právě tímto způsobem a signalizuje, že více hodnot se bude nacházet blíže střední hodnotě než u situace s vyšší Implied Volatilitou na úrovni 51.70%. Mohu si tak srovnat hodnoty pro strike 190 a zjistit, že pokud při vyšší Implied Volatilitě na úrovní 51.70% byla pravděpodobnost, že této ceny nebude dosaženo 65.24%, potom za nižší Implied Volatility na úrovni 30% činí tato pravděpodobnost 75.03%. Mohu tak použít i opačnou interpretaci, a to, že pro roční Implied Volatilitu ve výši 51.70% je na 34.755% pravděpodobné, že cena bude za měsíc vyšší než 190 USD, což je zcela jistě více pravděpodobné než pro roční Implied Volatilitu ve výši 30%, kdy je možnost proražení ceny 190 USD pravděpodobná pouze z 24.97%.

   Tyto výpočty pak definují pravděpodobnosti, kterých se mi nedostávalo při sestavení Teoretické ceny pozorované měsíční GS Long Call 180 opce na ATM strike a které si nyní mohu velmi pohodlně zjistit ve svém výpočetním excelovském sešitu a nejen to, mohu si také podle celkového obrazu Implied Volatility takové ceny jednoduše modelovat změnami jejich úrovně podle mých představ a nespoléhat se tak pouze na úsudek trhů. Jak se tedy mohu dopátrat pravděpodobností možných výskytů budoucích cen akcie GS v horizontu jednoho měsíce? Podle prozatím popsaných předpokladů, kterými jsou existence Normálního rozdělení cenových pohybů (fluktuace cen je zcela náhodná) se střední hodnotou 179.55 USD a hodnotou první standardní odchylky představující pohyb +/- 26.80 USD mohu za využití excelovské funkce zjišťovat pravděpodobnosti, s jakou se bude vyvíjet cenový pohyb do určité sledované hodnoty (oblasti). Pro mou zamýšlenou investici do GS Long Call na strike 180 při ceně akcie GS 179.55 USD pak bude pro mě klíčové definovat pravděpodobnosti v oblastech strike, které budou „mimo peníze“, tedy nad ATM strike na aktuální úrovni 180.

   Pro návod, jak takové pravděpodobnosti vlastně zjistit se současným potvrzením, že jsou mé výpočty a úvahy správné, se budu snažit zjistit, jaká je pravděpodobnost, že se za jeden měsíc bude cena akcie GS s předdefinovanou roční Implied Volatilitou ve výši 51.70% podle mé obchodní platformy pohybovat mezi strike 155 a 205. Proč zrovna tyto strike? Z výpočtu převodu roční Implied Volatility na její měsíční bázi jsem zjistil, že očekávaný pohyb s pravděpodobností náležející první standardní odchylce (68.20%) náleží rozsah pohybu +/-14.92%, což při aktuální ceně akcie GS 179.55 USD činí dolarový pohyb +/- 26.80 USD. Toto odpovídá rozpětí cen (179.55 USD +/- 26.80 USD) z cenového pásma 152.75 USD až 206.35 USD v horizontu jednoho měsíce a těmto mezním hodnotám pak nejblíže odpovídají strike 155 a 205. Mohu si pak svůj excelovský sešit poupravit pouze na sledování pravděpodobností hodnot podle zadaných strike (vymažu tedy řádky cenových úrovní mezi těmito strike, kde nejsou listovány opční kontrakty) a k nim přiřadit pravděpodobnosti s již poznanou funkcí jejího vyhledání =NORM.DIST                        

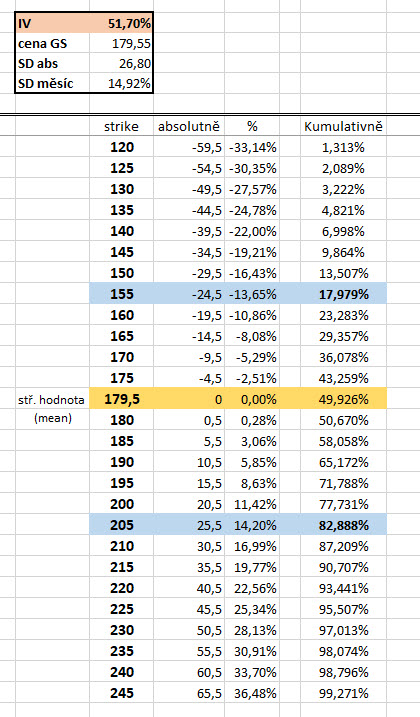
   Ve vypočítaném excelu s pravděpodobnostmi mohu zjistit, pokud použiji funkci =NORM.DIST, že s pravděpodobností 82.88 % budou ležet za měsíc možné cenové pohyby pod cenovou úrovní 205 USD. Graficky pak mohu tuto skutečnost zobrazit takto

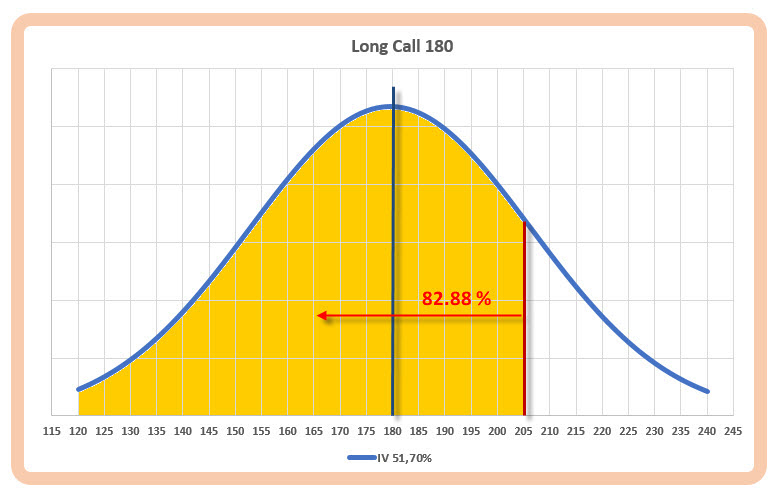
   Obdobně pak mohu výpočtem zjistit, pravděpodobnost pohybu za jeden měsíc do hodnoty 155 USD je 17.98%, stejně obdobně graficky pak mohu tuto skutečnost zobrazit takto  

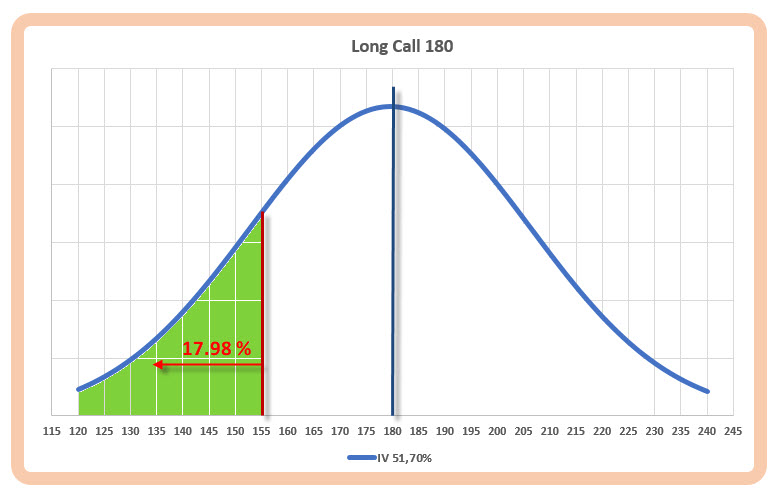
   Pokud tedy budu hledat pravděpodobnost, s jakou se mohou za měsíc ceny nacházet pod hranicí 205 USD a nad hranicí 155 USD, „odečtu od sebe obě tyto oblasti“ vyznačené v obrázcích výše.

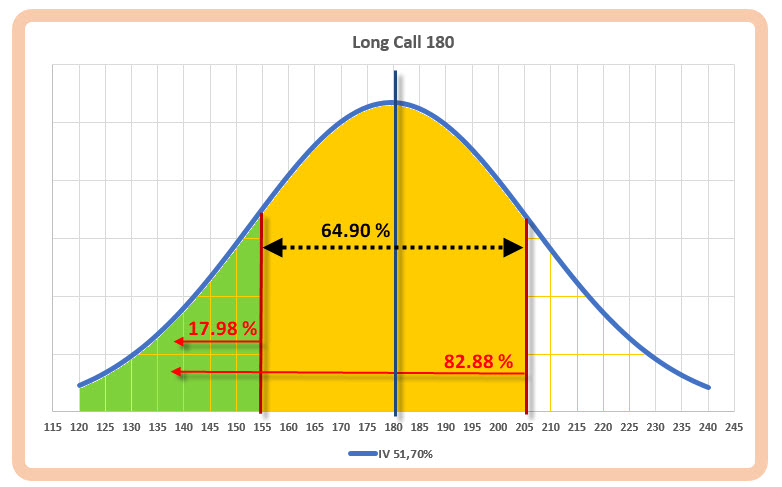
   Mohu pak jednoduše zjistit, že pravděpodobnost, že se cena bude za měsíc pohybovat mezi strike 155 USD a 205 USD je (82.88% – 17.98%) na úrovni 64.90 %, toto číslo pak opravdu odráží pohyb v rozsahu první standardní odchylky (68.20%) podle pravidla „tří sigma“ a mírná nepřesnost je pak způsobena zaokrouhlením vypočítaného možného cenového pohybu (+/-26.80 USD) do hodnot existujících strike nacházejících je +/- 25 USD nad současnou cenou akcie GS.

   Se stejnou logikou „odečítání oblastí pravděpodobností“ pak mohu svůj výpočet aplikovat také na svou úvahu o Teoretické pořizovací ceně opčního kontraktu GS Long Call 180 s expirací za jeden měsíc. Stačí si pak jen uvědomit, co budou jednotlivé pohyby do některé z cenových oblastí znamenat, jakou budou mít pravděpodobnost a jaký to bude mít vliv na jednoduchý matematický model výpočtu férové ceny opce, který jsem si vytvořil. Pokud provedu takové výpočetní operace, mohu je graficky zobrazit takto

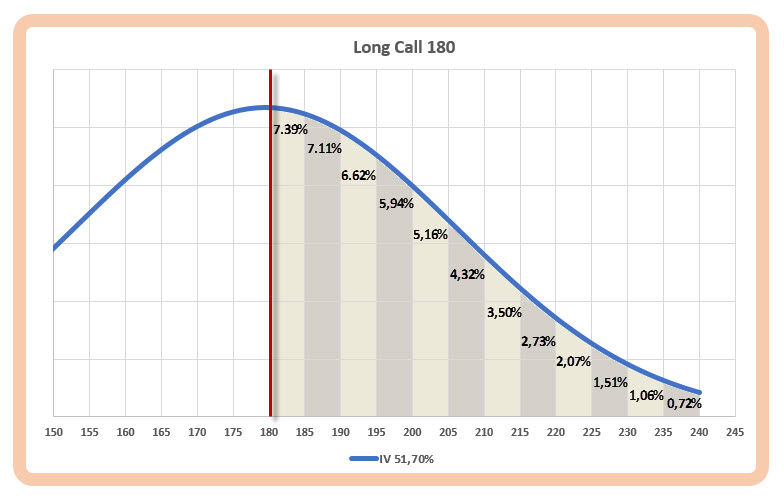
   Jednotlivé oblasti, reprezentované existujícími strike listovanými na opční burze, pak mohou vypadat tímto způsobem a reprezentovat pravděpodobnosti, že se za měsíc bude cena nacházet v takto vyznačených oblastech. Pokud je například oblasti růstu ceny na úrovně 195 USD – 200 USD přiřazena pravděpodobnost 5.94 %, tak s touto pravděpodobností mohu počítat za měsíc při expiraci opčního kontraktu pokud přijmu za své, že budoucí rozložení pohybů ceny bude mít Normální Rozdělení, tedy, že ceny budou náhodné, střední hodnota tohoto Normálního rozdělení je aktuální cena GS na úrovni 179.55 USD a hodnota první standardní odchylky je představována pohybem +/-26.80 USD za aktuální roční představy o Implied Volatilitě na úrovni 51.70%. Pokud se mi zdá, že necelých 6% pravděpodobnosti je velmi malé číslo, tak si musím uvědomit, při symetrickém tvaru Gaussovy křivky rozložení pravděpodobností, že stejnou pravděpodobnost kolem 6% má také pokles ceny do oblasti ve stejné vzdálenosti, tedy mezi 165 USD až 160 USD. Z celkového jakkoliv představitelného a uvěřitelně možného pohybu ceny GS (od úplného krachu ceny k nule až k růstu do plus nekonečna) pak dva cenové úseky 160 USD – 165 USD a 195 USD – 200 USD představují celkem slušných 12% pravděpodobnostních procentních bodů.

   Pohyby ceny akcie GS v nejrůznějších cenových oblastech pak znamenají samozřejmě nějaký cenový budoucí stav pro mou GS Long Call 180. Pokud budu tedy předpokládat pohyb ceny za měsíc až do oblasti mezi 195 USD a 200 USD reprezentované adekvátními strike (195 a 200), bude jisté, že v tomto případě bude mít má Long Call 180 opce hodnotu nejméně 1.500 USD (taková bude nejméně její Vnitřní Hodnota). Ve stejných intencích pak mohu vyhodnotit i zbylé oblasti z obrázku výše, pro které jsem vypočítal nějaké pravděpodobnosti. Pro budoucí pohyb do jednotlivých vzdálených oblastí mezi vyznačenými strike musím přijmout předpoklad, že v těchto jednotlivých mezích musí existovat další pravděpodobnost, kde cena nakonec za měsíc zůstane, protože jednoduše nemohu předpokládat, že při expiraci bude například přesně na ceně strike 195 USD a bude to s nějakou (nyní již vypočítanou) pravděpodobností znamenat profit +1500 USD. Pro úplné zjednodušení pak budu mít za to, že nejpravděpodobnější bude, že cena za měsíc zakončí někde uprostřed mezi strike jednotlivých oblastí. Je tak nyní patrné, že rozsah strike o šířce 5-ti bodů je značně nekomfortní pro takové odhady s měsíční periodou a patrně jednobodové pásma (…nebo dokonce půlbodové) by přinesly daleko preciznější odhady, takto jsou ale nyní opční kontrakty zalistovány, takto s nimi proto budu nucen pracovat. Mohu pak k vypočítaným pravděpodobnostem budoucího pohybu přiřadit jednotlivé Očekávané výnosy, které jsou patrné na obrázku níže.

   Tato tabulka pak shrnuje všechny zjištěné a popsané skutečnosti do jednoho konečného výstupu – Teoretické ceny opčního kontraktu GS Long Call 180 s expirací za jeden měsíc podle velmi zjednodušeného „matematického modelu“.  Jednotlivé oblasti vymezené strike, kde by mohla cena akcie GS zakončit, jsou na prvním řádku (1) a příslušné pravděpodobnosti dosažení těchto oblastí jsou pak na druhém řádku (2). Vnitřní hodnota GS Long Call 180 opčního kontraktu (profit) s předpokladem, že cena zakončí uprostřed sledované oblasti je zachycena na třetím řádku (3). Nakolik přispěje svou pravděpodobností do celkového výpočtu Teoretické ceny GS Long Call 180 opce příslušná předpokládaná oblast ceny je uvedeno na čtvrtém řádku (4), celkový profit dosažení cenové oblasti je „zvážen“ pravděpodobností, s jakou tato oblast bude dosažena. Například pro oblast možného pohybu do oblasti 195 USD – 200 USD (červený obdélník) je přiřazena pravděpodobnost 5.94% a případný profit na opci při dosažení ceny 197.50 USD (střed oblasti) by byl +1.750 USD, po zvážení pravděpodobností by pak celkový příspěvek do Teoretické ceny činil (+1.750 USD * 5.94%) částku +104 USD. V silně orámované buňce je pak celková rekapitulace výpočtu (součet cenových příspěvků podle jednotlivých vah z řádku (4)), ve které mohu zjistit, že mnou vypočítaná férová Teoretická cena opčního kontraktu GS Long Call 180 s expirací za měsíc by měla činit 995.82 USD. V obrázku v článku výše pak mohu pozorovat, že nabízená cena s opční platformy je 1.065 USD, tedy zhruba o 70 USD vyšší. Tento rozdíl mohu přisoudit sofistikovanějšímu výpočetnímu modelu opční ceny organizátorem trhu, strukturou nabídky a poptávky a dalšími případnými vlovy, na obecném obrysu ceny se ale víceméně s představou trhů shoduji.

   Aktuální hodnota Implied Volatility na úrovni 51.70% je opravdu vysoká a způsobuje, že opční kontrakty jsou drahé. Je to způsobeno právě rozložením pravděpodobnosti, že cena může v budoucnosti dosáhnout do vzdálenějších oblastí a toto se zpětně promítá do ceny opčního kontraktu. Mohu si pak vyzkoušet jednoduché modelování, kdy ponechám všechny parametry jak jsou a budu se pokoušet testovat takto jednoduše vypočítanou cenu opčního kontraktu změnou Implied Volatility. Pro hodnotu Implied Volatility na úrovni 30% pak mohu vysledovat cenu opčního kontraktu GS Long Call 180 s měsíční expirací podle mého excelu takto.                                                                                                   

   Z obrázku je patrné, férová cena při této Implied Volatilitě 30% by měla být pouze 603.36 USD. Z tabulky pravděpodobností dosažení jednotlivých cenových oblastí je pak patrné, že značně narostla pravděpodobnost pohybů do bližších oblastí aktuální ceně, zatímco vzdálenější cenová pásma mají pravděpodobnost zanedbatelnou, tento „chabější“ cenový výhled se tak promítá také do ceny opčního kontraktu, a to pouhou změnou náhledu na hodnotu Implied Volatility. Mohu si pak tento výpočet ověřit v praxi. Na úrovni Implied Volatility kolem 30% se v nedávné historii nacházela akcie GS 26.2.2020, mohu pak tuto úroveň odečítat z obrázku jejího průběhu.

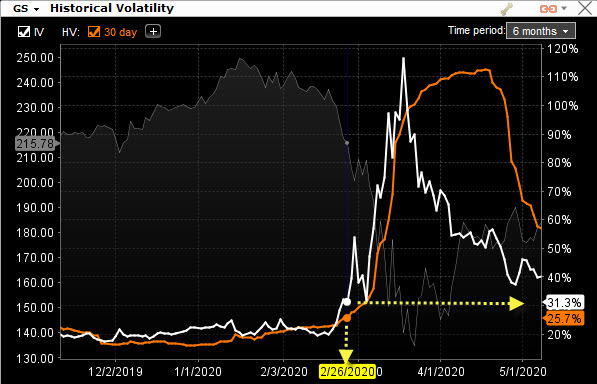
   Pro tento den si mohu nechat zobrazit historické ceny opčních kontraktů podkladové akcie GS s expirací za třicet dnů pomocí analytické aplikace thinkorswim.  

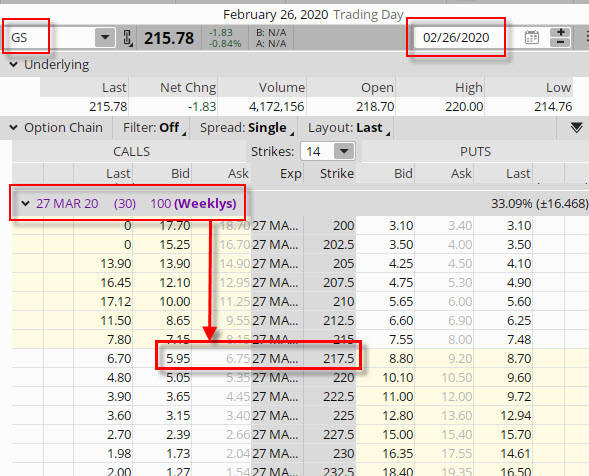
    Mohu vypozorovat, že cena GS Long Call opčních kontraktů na ATM strike se pohybuje v pásmu mého zjednodušeného výpočtu (603.36 USD) na hodnotě Bid/Ask v rozpětí 595 USD – 675 USD. Mohu si tak změnami hodnoty Implied Volatility modelovat velmi jednoduché situace, jejich výsledek pak bude mít očekávaný průběh zcela závislý na úrovni pravděpodobností, s jakou bude možné dosáhnout určitá cenová pásma pro obchodovaný podklad. Na obrázku níže je pak taková simulace zobrazena.

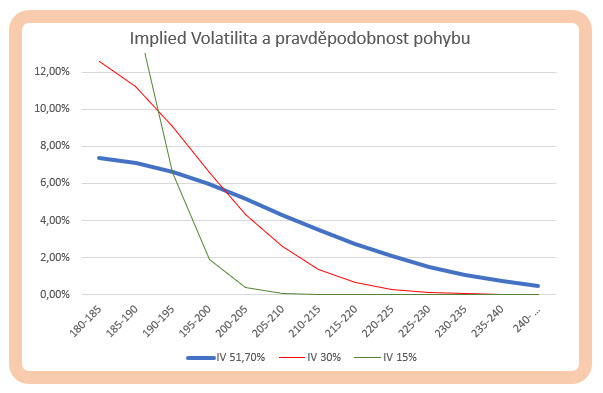
   Modrá křivka grafu zobrazuje jednotlivé pravděpodobnosti při Implied Volatilitě na úrovni aktuálních 51.70%, křivka je mírně sestupná a její pozvolnější průběh zobrazuje zejména vyšší pravděpodobnosti, že se ceny můžou vychýlit v měsíčním horizontu i do vzdálenějších oblastí, naproti tomu extrémně nízká Implied Volatilita na úrovni 15% zobrazena zelenou křivkou naznačuje vysoké pravděpodobnosti, že cena zůstane v budoucnosti vyjádřené jedním měsícem  v okolí aktuální ceny, kdežto výletům do vzdálenějších cenových oblastí je přisuzována pravděpodobnost velmi minimální.

Normální nebo Lognormální…

   Fisher Black a Myron Scholes vycházeli při konstrukci oceňovacího opčního modelu ze stejných principů a vlastností Normálního rozdělení pravděpodobnosti náhodných jevů, což není nic převratného k pochopení a má také svou logiku. Pokud budu schopen přiřadit náhodnému jevu číslo – pravděpodobnost výskytu, pak již bude jenom na sofistikovanosti metody tohoto přiřazování, jaký nakonec bude celkový výsledek popisu chování náhodných jevů a také jeho interpretace a v konečném důsledku také aplikace do běžné reality, například obchodování. Ve své definici předpokladů pro svůj oceňovací opční model pak měli za to, že cenové pohyby podkladového aktiva budou zcela náhodné a nebude tak existovat žádná možnost umělé manipulace s trhy. Pokud budou cenové pohyby podkladového aktiva zcela náhodné, tak v jejich procentním vyjádření to bude znamenat, že tyto pohyby budou mít pravděpodobnosti s vlastnostmi připadajícími Normálnímu Rozdělení, kde střední hodnota (mean) bude představována aktuální cenou podkladového aktiva (akcie, futures, indexu…). Pokud mám soubor výskytů náhodných jevů – cenových pohybů podkladu s Normálním Rozdělením a danou střední hodnotou, jsem schopen stanovit hodnotu standardní odchylky. Hodnota standardní odchylky mi pak popisuje pravděpodobnost, kde se může jakákoliv náhodná cena nacházet. Pokud znám hodnotu Implied Volatility, mohu stanovit hodnotu standardní odchylky a mohu tak počítat, kde se budoucí ceny mohou nacházet, což bylo náplní předcházejících řádků. Hodnotu Implied Volatility vyjádřené v procentech si pak mohu převádět na různé časové úseky, například na denní bázi, což jsem již několikrát na tomto webu i v tomto článku naznačil. Pravděpodobnosti odvozené z principů Normálního Rozdělení a vyjádřené pro opčního obchodníka hodnotou Implied Volatility pak způsobují, že Implied Volatilita je z obecného pohledu funkcí opční ceny, čím je Implied Volatilita vyšší, tím jsou také vyšší ceny jednotlivých kontraktů pro daný okamžik, pro danou expiraci, pro daný strike a pro stejnou aktuální cenu podkladu. Taková úvaha má však jednu logickou vadu, kterou je symetrické rozložení pravděpodobnosti, jak jsem jej popisoval v textu výše. Mohu si konkrétně představit, že existuje akciový titul, který se nyní obchoduje za 20 USD a jistě existuje nějaká (byť velmi malá) pravděpodobnost, že se cena bude za jeden rok nacházet na úrovni 45 USD a posílí tak o +25 USD. To není nic nepředstavitelného a mohu takové pravděpodobnosti přiřadit například hodnotou desetiny procenta (0.10%). Jestliže existuje taková pravděpodobnost pro růst, musí z povahy symetrického rozložení existence náhodných pohybů Normálního Rozdělení (…a z tvaru Gaussovy křivky…) existovat také stejná pravděpodobnost o velikosti desetiny procenta, že cena za jeden rok klesne o -25 USD. Toto je ale nemožné, protože by se cena akcie dostala do záporných hodnot (-5 USD), což je v reálném obchodování nemožné, cena podkladů může být minimálně nulová. Tuto skutečnost je také nutno respektovat při výpočtu ceny opčního kontraktu a je jedno, jaký výpočetní matematický model použiji, tuto vlastnost cenového pohybu podkladu pak také samozřejmě respektuje Black-Scholesův výpočetní model.

   Dalším předpokladem pro stanovení férové opční ceny je pak skutečnost, že zobrazená Implied Volatilita, kterou mám možnost pozorovat ve své opční platformě, bude konstantní po celou dobu života opčního kontraktu. Je jasné, že toto je nemožný a nesplnitelný předpoklad z pohledu dialektiky trhu podkladu, ale je to myšleno tak, že nyní, když sestavují výpočet opční ceny opčního kontraktu a zakomponuji do něj nějakou hodnotu Implied Volatility, bude vypočítaná cena zobrazovat úroveň, kterou by měla za počítaný časový úsek při této Implied Volatilitě. Pokud dnes pozoruji Implied Volatilitu na úrovni 51.70%, tak Long Call opce „na penězích“ s měsíční expirací bude mít hodnotu 1.000 USD, pokud ale budu do svého výpočetního modelu počítat s úrovní Implied Volatility na úrovni 30%, bude cena této měsíční opce 600 USD. Okamžitý pokles Implied Volatility z hodnoty 51.70% na úroveň 30% při neměnnosti jiných vlivů na cenu podkladu tak znamená okamžitý rozdíl – 400 USD a bude pak záležet, jakou opční pozici jsem zaujal a jaký to představuje finanční dopad (zisk nebo ztrátu).

   Zobrazená Implied Volatilita na nějaké úrovni vyjadřuje pravděpodobnost pohybu ceny v nějakém budoucím čase. Kromě toho, že takový pohyb nemůže být nižší než nula, předpokládají matematické výpočetní modely, že tento budoucí pohyb nebude symetrický pro růst i pokles z důvodů „compounding efektu“, který jsem již popisoval v tomto článku o pákových Volatility ETF. Jeho základním principem je existence skládaného výnosu, který si mohu nasimulovat v Excelu pomocí funkce =BUDHODNOTA, jako na níže uvedeném obrázku, kde jsem zobrazil fiktivní zhodnocení nákupu jedné akcie GS za pořizovací cenu 180 USD s předpokladem, že tato akcie každý den zhodnotí +1% ze své ceny nebo naopak každý den ze své hodnoty -1% ztratí.    

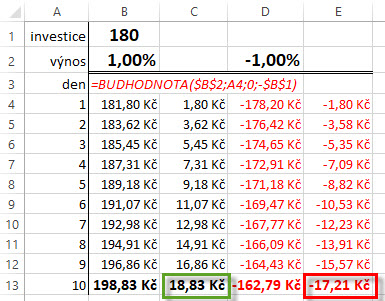
   Nárůst hodnot mé investice zhodnocující každý den o plus jedno procento (sloupec černých čísel) vlivem efektu skládaného růstu způsobil, že po deseti dnech má investice posílila o +18.83 USD (jak jsem k výpočtu dospěl je patrné s červeně zobrazené excelovské funkce). Oproti tomu, vlivem stejných efektů, má investice ztrácející mínus jedno procento denně vykazuje po stejně dlouhém období deseti dnů ztrátu pouze -17.21 USD, ztráta je tedy +1.62 USD mírnější. Tento „compounding efekt“ tak způsobuje nesymetrické chování poklesů a růstů a pokud bych sledoval, jaké rozdělení mají cenové pohyby v daném období vlivem tohoto efektu, zjistil bych, že takové ceny mají Lognormální rozdělení. V mém konkrétním případě, přestože tedy jednotlivé procentní cenové pohyby akcie GS mají zcela náhodnou povahu a tyto pohyby mají Normální Rozdělení, vlivem „compounding efektu“ bude celkové zhodnocení výnosu z investice do akcie GS v budoucnosti mít Lognormální Rozdělení.

   Lognormální rozdělení těchto budoucích cen tak „zabíjí dvě mouchy jednou ranou“. Základem logaritmu musí být číslo větší než nula a tím je ošetřen pokles ceny podkladů do záporných hodnot a z povahy logaritmování naměřených hodnot ošetřuji „compounding efekt“. Vliv Lognormálního rozdělení cen podkladového aktiva v budoucnosti, například v expirační den mého měsíčního opčního kontraktu, musí být opět součástí úvah při konstrukci matematického oceňovacího modelu dávajícímu si za cíl stanovit cenu opčního kontraktu, který expiruje v nějaké předem definované budoucnosti. Pokud uvažuji o ceně opčního kontraktu a zhodnocením investice do tohoto nástroje podle údajů o Implied Volatilitě například na úrovni 30% ročně, musím si uvědomit, že oceňovací modely počítají nejen se skutečností, že cena nemůže klesnout pod nulu, ale hlavně, že vlivem „compounding efektu“ má tendenci více zhodnotit při růstu ceny podkladu do expirace než při jejím poklesu. Obrazem této skutečnosti je pak praktický dopad do cen opčních kontraktů, které jsou na strike v určité vzdálenosti nad současnou cenou (Call) obecně vyšší než na strike se stejnou vzdáleností pod současnou cenou (Put). Toto si nakonec mohu také nasimulovat pomocí kalkulátorů opčních cen, například toho, který jsem již nabízel v excelovském provedení na tomto webu a je ke stažení zde. Mohu pak pro titul s aktuální cenou 180 USD při roční Implied Volatilitě 30% sledovat ceny opčních kontraktů Call a Pout se strike ve vzdálenosti +/-5 USD od současné ceny s expirací za třicet dnů.

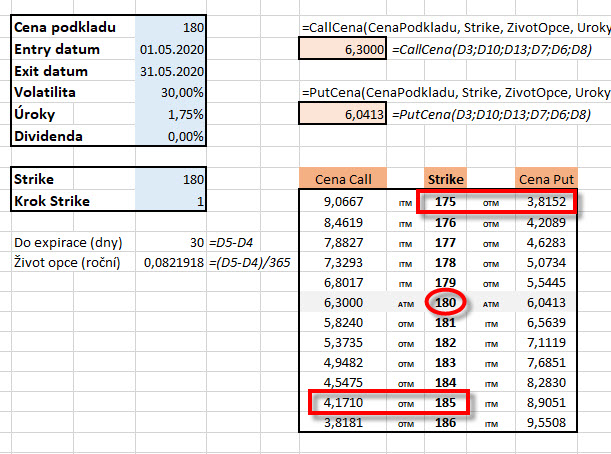
    Z obrázku z výpočtu podle Black-Scholesova modelu vyplývá, že cena opce Call na strike 185 má hodnotu 417 USD, kdežto cena opce Put na strike 175 má hodnotu pouze 381 USD. Rozdíl -36 USD je způsoben právě těmito efekty zabudovanými do výpočtu opční ceny. Správnost výpočtu mohu ověřit také na aplikaci pro výpočet opční ceny mého brokera Interactive Brokers, který vypočetl za stejných vstupních podmínek cenu Call opce na strike 185 takto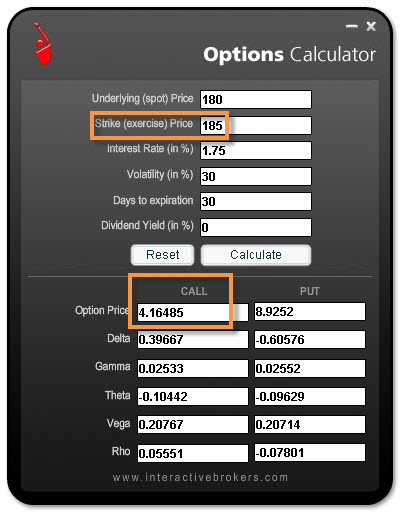       

   Ve stejném smyslu, pro ověření výpočtu, pak tato aplikace vypočítala cenu Put opčního kontraktu na strike 175 takto

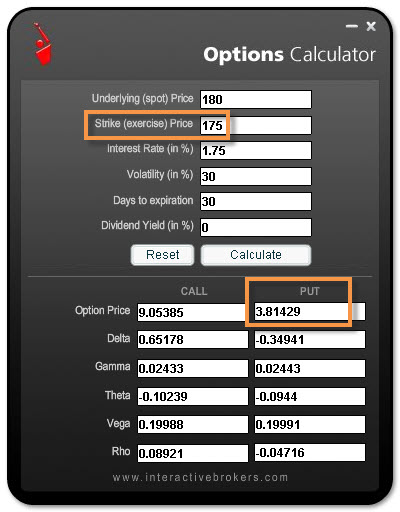
   Výpočty jsou identické, jako z mého excelovského sešitu.

    Sdělení, že „…čím je vyšší Implied Volatilita, tak tím je vyšší cena opčního kontraktu…“ by mohlo po přečtení výše uvedeného textu nabýt na větší plastičnosti v nějakých konkrétnějších teoretických souvislostech, žádné jiné ambice si napsaný text nedělal, žádné hlubší teoretické úmysly jsem do něj nevkládal. To, že si mohu jednotlivé souvislosti a vztahy nakonec také jednoduše namodelovat v nejběžnějším výpočetním software (Excel) může odebrat takovému teoretizování povahu zbytečně akademického přístupu. Není to vlastně nic jiného, než se snažit zkrotit náhodu a nevyzpytatelnost budoucnosti a dát těmto jevům základní matematické obrysy a alespoň obecně uchopitelné použití…:c)     

   Komentáře a příspěvky k tomuto článku prosím směrujte do Diskuzního fóra do tohoto vlákna :c)