V posledním článku dluhopisové minisérie Dluhopisy – XV. jsem popsal jednoduchý obchod s nákupem dluhopisu a jeho zajištění pomocí odpovídajícího dluhopisového futures. Zvolený modelový obchod nedoprovázela žádná hlubší úvaha o vlastnostech zvoleného dluhopisu a byly tak patrné pouze základní vztahy mezi vývojem úrokových sazeb, cenou dluhopisů a hodnotou odpovídajícího dluhopisového futures. Cílem obchodu bylo inkasovat kupónový výnos a předejít změně ceny nakoupeného kupónového dluhopisu pomocí shortování dluhopisového futures, toto mělo kompenzovat změnu ceny podkladového dluhopisu vlivem změny tržních úrokových sazeb odpovídajících dluhopisů s obdobnou dobou do splatnosti na úrokových trzích. Ukázkový obchod potvrdil možnost využít takto sestavené kombinace k sanaci pohybu ceny nakoupeného dluhopisu, nicméně bylo patrné, že k dokonalosti tomu něco chybělo. Mohu tak přemýšlet, jak nabyté znalosti o vlastnostech dluhopisů z článků na tomto webu využít pro lepší pochopení fungování takového obchodu nebo dokonce využít nových poznatků k tomu, aby takový obchod mohl lépe pracovat v můj prospěch.

   Je jisté, že každý pořízený dluhopis reaguje na změnu odpovídajících úrokových sazeb jiným způsobem. Základními vlastnostmi, které toto chování odrážejí, jsem se zabýval v článku Dluhopisy – VIII., který popisoval především durací dluhopisů, způsob jejího výpočtu a možnosti její praktické aplikace. Durace byla popsána jako průměrná doba do splatnosti dluhopisu s tím, že postup výpočtu poprvé popsal Frederic Macaulay, proto je někdy také označována jak Macaulayova durace. Tuto duraci mají vyšší kupónové dluhopisy s delší dobou do splatnosti než s kratší dobou do splatnosti, pokud budu mít stejné dluhopisy se stejnou dobou do splatnosti, potom vyšší duraci budu pozorovat u dluhopisů s nižším kupónem. Toto zjištění je prazákladem k výběru investice do kupónového dluhopisu. Macaulayova durace, tedy průměrná doba do splatnosti je sice fajn věc, ale obchodníci s dluhopisy chtějí její praktičtější interpretaci. Proto, vydělením hodnoty Macaulayovy durace (průměrné doby do splatnosti) aktuální tržní úrokovou sazbou, získám hodnotu Modifikované durace, která mi v procentech naznačuje, o kolik se změní hodnota mého dluhopisu, pokud se změní tyto úrokové sazby o jeden procentní bod. Tento údaj v procentech je pak výrazně pochopitelnější a praktičtější pro další obchodní úvahy o nakládání s dluhopisy, navíc tento procentní údaj o duraci pak mohu pozorovat v běžných obchodních platformách. Nemohu si pak odpustit příměr s cenou opčních kontraktů a vypočítanou hodnotou Delta, která popisuje, o kolik se změní cena tohoto opčního kontraktu, pokud se změní cena podkladového aktiva o +1.00 USD. Modifikovaná durace tak odráží podobný cenový efekt, popisuje, nakolik se změna tržních úrokových sazeb promítne do ceny kupónového dluhopisu a snaží se jej kvantifikovat.

Konvexnost (Convexity)

   U příkladu s opčními kontrakty setrvám, tato paralela se mi totiž přímo nabízí. Pokud byla hodnota Delta opčního kontraktu první derivací cenové funkce opčního kontraktu a vyjadřovala závislost ceny opce na pohybu podkladového aktiva o +1.00 USD, potom hodnota Macaulayovy durace, kterou Frederic Macaulay získal derivováním cenové funkce kupónového dluhopisu, zobrazuje závislost ceny dluhopisu na aktuálních tržních úrokových sazbách (přepočítáno následně pro zjištění Modifikované durace). Mohu tak tuto duraci přirovnat k Delta opčního kontraktu. Poznání samotné Delta opce je pro opčního obchodníka opravdu hodnotný poznatek, pokud ale chci jít více do hloubky, měl bych toto poznání obohatit o zjištění, jak rychle se hodnota Delta bude měnit, cenová funkce opčního kontraktu není nic lineárního a dynamika hodnoty Delta se samozřejmě mění tak, jak se mění tvar této cenové funkce. K měření rychlosti změny hodnoty Delta opčního kontraktu se používá druhá derivace cenové funkce opčního kontraktu a výsledkem tohoto derivování je zjištění hodnoty Gamma opčního kontraktu. V článku o Gamma jsem tuto hodnotu přirovnal k tachometru, který je přišroubován ke každé hodnotě Delta pro daný opční kontrakt a měří rychlost, jakou se bude Delta měnit v závislosti na změně ceny podkladového aktiva.

   Cenová funkce kupónového dluhopisu není rovněž nic lineárního, ale má „vypouklý tvar“ a naznačuje, že durace bude mít na cenu pokladového dluhopisu v různých chvílích různý vliv. Na obrázku níže je simulace cenové křivky desetiletého dluhopisu Ford s kupónem 6.625%, který jsem si vypůjčil z článku Dluhopisy – VIII..

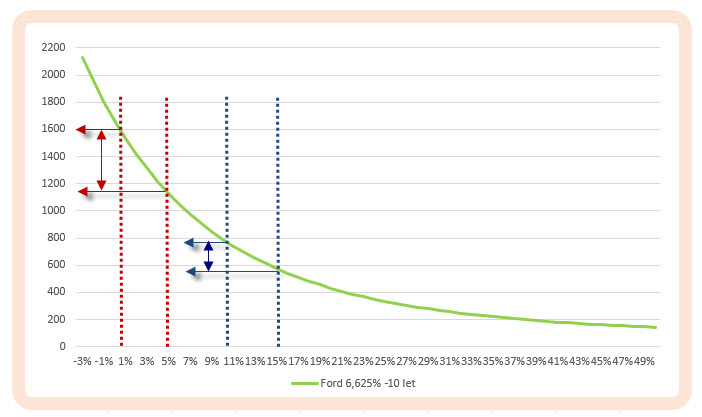
   Osa x představuje možné tržní úrokové sazby, na ose y je vypočítaná odpovídající cena dluhopisu. Za přijatou „dluhopisovou pravdu“ pak pokládám pohled na cenovou křivku, která zobrazuje základní závislost, tedy že při růstu úrokových sazeb (směrem doprava) se cena dluhopisu snižuje a naopak. Mohu ale také pozorovat, že tato závislost není lineární. Změna úrokových sazeb z 1% na 5% (červené šipky) je doprovázena výrazně větší změnou ceny dluhopisu než je obdobná změna úrokových sazeb z 11% na 15% (modré šipky). Strmost je na levé části křivky jednoduše vyšší, než je na pravé straně křivky, kde se hloubka této závislosti podstatně snižuje. Není asi praktické, abych si při výběru dluhopisů vykresloval tuto cenovou křivku a odhadoval, podle aktuálních úrokových sazeb, jakým způsobem bude jejich změna pohybovat cenou pozorovaného dluhopisu. Pokud by mělo padat obchodní rozhodnutí pro podobné dluhopisy, určitě by se mi hodil nástroj, který by takovou situaci popisoval. Stejně jako u opčních kontraktů se stejnou Delta pro podobné typy kontraktů mohu svou pozornost zaměřit na Gamma, abych se rozhodoval, který z opčních kontraktů mě obdaří vyšší dynamikou pohybu. Opce s Delta +35 a Gamma 15 znamená, že při pohybu o +1.00 USD bude mít novou Delta +50 a bude výrazně dražší, než ve stejném případě s Gamma 6, kdy Delta této opce posílí pouze na hodnotu Delta +41 a nebude mít takovou cenu, jako opční kontrakt s vyšší Gamma. Výše jsem uvedl, že Gamma je druhou derivací cenové funkce opčního kontraktu a zachycuje dynamiku změny její ceny, pomohlo by mi tedy nyní zkoumat, jak tuto dynamiku zachytit u změny ceny kupónového dluhopisu. Druhá derivace cenové funkce kupónového dluhopisu takovou změnu zachycuje a její výsledek je popisován jako Konvexnost (Convexity) dluhopisu. Ve zkratce, první derivací cenové funkce kupónového dluhopisu podle úrokové míry je hodnota Macaulayovy durace a zachycuje závislost cenového pohybu dluhopisu na změně úrokových sazeb, druhou derivací cenové funkce kupónového dluhopisu je hodnota Konvexnosti a popisuje rychlost této cenové změny. Ve vzorcích se nevyžívám, nicméně pro ucelení problematiky doprovodím tuto úvahu také o matematickou interpretaci, přestože k výstupní informaci nebude potřeba žádný z těchto vzorců použit. Vzorec pro výpočet první derivace cenové funkce kupónového dluhopisu je níže, SH je současná hodnota dluhopisu, úrok je aktuální tržní úroková sazba, C je hodnota kupónu a FV je Face Value dluhopisu:

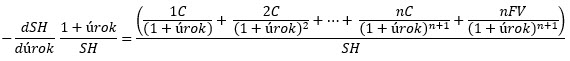
   Toho vzorce se není třeba nějak obávat, protože nic derivovat prakticky nebudu, musím jenom vědět, že výraz na pravé straně je Macaulayova durace, takže: 

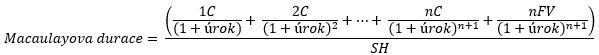
   První derivací tak stanovím tuto hodnotu průměrné doby do splatnosti dluhopisu (Macaulayovu duraci), tedy číslo, jehož velikost mi popisuje citlivost ceny kupónového dluhopisu na změnu úrokových sazeb. Pokud chci získat hodnotu Konvexnosti, tedy dynamiku změny durace způsobenou zakřivením (proměnlivou strmostí) cenové křivky dluhopisu, podrobím cenovou rovnici také druhé derivaci podle aktuální úrokové sazby:

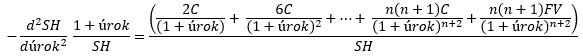
   Opět nebudu v praxi nic nadvakrát derivovat podle úrokové sazby, jenom budu chtít vědět, že výraz na pravé straně rovnice představuje Konvexnost kupónového dluhopisu, potom tedy:

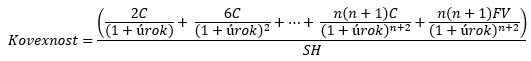
   Výsledkem výpočtu Konvexnosti bude opět číslo, které bude charakterizovat dynamiku durace a bude pomáhat ke zjištění budoucí ceny dluhopisu v závislosti na změně aktuálních tržních úrokových sazeb. Výsledkem mého snažení při hledání budoucí cenu dluhopisu při určitém pohybu úrokových sazeb tak budou dvě výstupní hodnoty z nadepsaných vzorců – Macaulyvoa durace a Konvexnost, když obě tyto hodnoty mi poskytne má obchodní platforma a nebudu muset provádět složité derivace. Nabízí se tak otázka, proč jsem celou věc tak významně komplikoval prezentováním a popisováním složitých vzorců, když mohu jednotlivé hodnoty velmi jednoduše získat z obchodní platformy? Odpověď má dva základní důvody, mohu si pomocí těchto dvou zjištěných hodnot přesněji vypočítat budoucí cenu dluhopisu při dané změně úrokových sazeb a také si mohu pomocí tohoto výpočtu interpretovat vliv Konvexnosti na tento vypočítaný výsledek. K provedení tohoto výpočtu pak opět použiji přirovnání k hledání budoucí ceny opčního kontraktu, které jsem popisoval (v krajně nezáživném) článku Delta Neutral – VI. a v tam popisovaném výpočtu budoucí ceny opčního kontraktu navážu a pokusím se tento postup aplikovat na hledání budoucí cenu dluhopisu.

   Základním předpokladem k takovému výpočtu hledání budoucí ceny kupónového dluhopisu bude zjištění, že znám jeho aktuální cenu, předpokládám, že existuje nějaká cenová funkce, která popisuje její budoucí vývoj podle nějakého parametru (změna úrokových sazeb), znám první derivaci cenové funkce podle tohoto parametru (Macaulayova durace) a znám také druhou derivaci cenové funkce podle tohoto parametru (Konvexnost). Pokud mám tyto hodnoty k dispozici, mohu matematicky celkem přesně aproximovat budoucí cenu dluhopisu podle změny úrokové sazby pomocí Taylorova polynomu druhého řádu (Taylorova rozvoje). Tento vzorec by pak v nějakém zjednodušení mohl vypadat takto:

   Opět to nevypadá přívětivě, ale jednoduše to znamená, že budoucí cena dluhopisu BH při změně tržních úrokových sazeb úrok bude tvořena současnou hodnotou cenou dluhopisu SH, která bude upravena o první derivaci jeho cenové funkce upravenou o změnu úrokových sazeb a následně upravena o polovinu druhé derivace cenové funkce upravenou o druhou mocninu změny úrokových sazeb, reziduum je aktuálně nepodstatná hodnota. Nyní vím, že první derivace cenové funkce je Macaulayova durace a druhá derivace je hodnota Konvexnosti, potom si tento vzorec mohu představit takto:

   Výše uvedený vzorec tedy mohu velmi příjemně zjednodušit a v jednotlivých úpravách převést na výpočet změny cenu dluhopisu (BH – SH) vlivem durace a Konvexnosti takto:

   Uvedl jsem, že hodnotu Durace a Konvexnosti pohodlně zjistím ve své obchodní platformě (takže opravdu žádné derivování) a z tohoto pohledu je potom výpočet budoucí ceny dluhopisu pouze jednoduchá matematika. Na obrázku níže je americký vládní dluhopis zobrazený v platformě TWS mého brokera Interactive Brokers.

   Mohu vypozorovat, že dluhopis se splatností 30.9.2030 a kupónem 4.625% p.a. se aktuálně nabízí za 102.994% Face Value, investice ve výši 1000 USD by pak představovala výdaj 1029.94 USD. Mohu vypozorovat, že hodnota Konvexnosti je 35 a hodnota Modifikované durace je 5.65%. Z hodnoty durace by se dalo usoudit, že pokud se aktuální úrokové sazby pohnou o +/-1% (+/-100 bazických bodů), změní se cena dluhopisu o +/-5.65%. Neznám ale tvar cenové křivky tohoto dluhopisu a nevím, jak bude tuto cenovou změnu deformovat právě její tvar, tuto deformaci by pak mohla zachycovat právě hodnota Konvexnosti. Než zapojím do výpočtu takto získaná data, musím si uvědomit, že zobrazená durace z platformy TWS je Modifikovaná durace, která byla zjištěna z hodnoty Macaulayovy durace vydělené aktuální úrokovou sazbou.

   Musím si proto nejdříve převést Modifikovanou duraci z TWS na Macaylayovu duraci algebraickou úpravou výše uvedeného zlomku:

   Zjištěná hodnota Macaulayovy durace tak bude závislá na znalosti Modifikované durace z platformy TWS ve výši 5.65% a aktuální tržní úrokové míry pro daný dluhopis. Tuto mohu zjistit z veřejných zdrojů a mohla by pro dnešní den vypadat například takto:

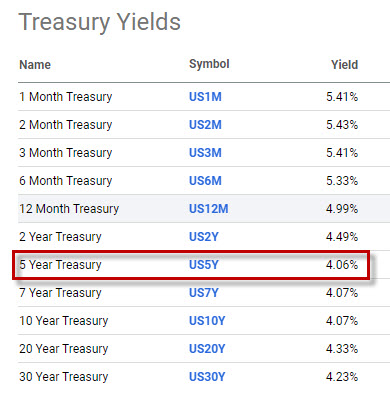
   Mému šestiletému dluhopisu by mohla odpovídat tržní úroková sazba ve výši 4.06% p.a., tuto tedy aplikuji do výpočtu průměrné doby do splatnosti dluhopisu – Macaulayovy durace:

   Mám tak k dispozici aktuální cenu dluhopisu ve výši 1029,94 USD, hodnotu Macaulayovy durace ve výši 5,879 a Konvexnost s hodnotou 35. Mohlo by mě pak zajímat, o kolik se změní cena mého dluhopisu, pokud tržní úrokové sazby klesnou o -0,50%. Budu se tak snažit aplikovat na tento výpočet právě tento zjednodušený vzorec níže:

   Z tohoto zjednodušeného vzorce pak vyplývá, že budoucí změna ceny kupónového dluhopisu (BH – SH) bude znamenat formování současné ceny SH kupónového dluhopisu díky Duraci a také Konvexnosti, mohu pak vzorec výpočtu z obrázku výše použít a dosadit zjištěné údaje ke zjištění, o kolik se změní cena mého kupónového dluhopisu, pokud aktuální úrokové sazby klesnou o půl procentního bodu:

   Pokud tedy dojde k poklesu úrokových sazeb o -0,50%, bude můj dluhopis obdařen změnou ceny o +30.725 USD a bude mít cenu (1029,94 USD + 30.275 USD) na úrovni 1060,215 USD. Mohl bych pak naopak chtít zjistit, jak se bude cenově dařit mému dluhopisu, pokud by tržní úrokové sazby narostly o +0,50% při stejných parametrech Macaulayovy durace a Konvexnosti:

   Opačný pohyb úrokových sazeb (jejich růst) bude doprovázen poklesem ceny kupónového dluhopisu, tento by díky Duraci a Konvexitě ztratil na ceně -29.825 USD a jeho cena by pak byla (1029,94 USD – 29.825 USD) na úrovni 1000,115 USD.

   Co si mohu o vztahu Konvexnosti, Durace, změny úrokových sazeb a ceny kupónového dluhopisu vlastně odnést? Durace odráží citlivost změny ceny dluhopisu na změnu úrokových sazeb (Durace je první derivací cenové funkce), ale Konvexnost tento vztah Durace x Cena dluhopisu x změna úrokových sazeb koriguje díky skutečnosti, že cenová funkce kupónového dluhopisu není lineární, ale vykresluje křivku z obrázku v úvodu článku (Konvexnost je druhou derivací cenové funkce). Pokud bude pohyb úrokových sazeb malý, bude vliv Konvexnosti na cenu dluhopisu zanedbatelný, s větším pohybem úrokových sazeb se ale úprava ceny dluhopisu díky Konvexnosti zvýrazní. Při pohledu na tvar cenové křivky a způsob výpočtu budoucí hodnoty kupónového dluhopisu je patrné, že pokud budou úrokové sazby klesat, bude se toto odehrávat na části zvyšující se strmosti cenové křivky, tedy hodnota Konvexnosti bude k ceně „přidávat“ a naopak, při růstu úrokových sazeb se bude toto odehrávat na plošší části cenové křivky a Konvexnost bude tento pokles „brzdit“. Mohu tak Konvexnost zapojit do rozhodování o pořizování dluhopisu a mého očekávání spojeného s pohybem tržních úrokových sazeb. Pokud budu mít k dispozici podobné dluhopisy s podobnými parametry (splatnost, výnos do splatnosti, kupón, rizikovost…) a budu očekávat kapitálový výnos z dluhopisu spojený s masivním poklesem úrokových sazeb, bude pro mě vhodnější variantou výběr dluhopisů s vyšší Konvexností. Při výběru dluhopisu, od kterého budu očekávat menší reakci na pohyb úrokových sazeb mohu při výběru z portfolia nabízených dluhopisů se stejnými nebo výrazně podobnými vlastnosti vsadit na dluhopis s nižší Konvexností.

   Vše také mohu zasadit do pohledu na své dluhopisové portfolio, kdy si mohu nechat zobrazit Duraci společně s Konvexností celého dluhopisového portfolia a z těchto údajů usuzovat na cenový pohyb portfolia v závislosti na změně úrokových sazeb. Na obrázku níže je zobrazena Konvexnost dluhopisového portfolia z analytického nástroje Risk Navigator platformy TWS brokera Interactive Brokers.

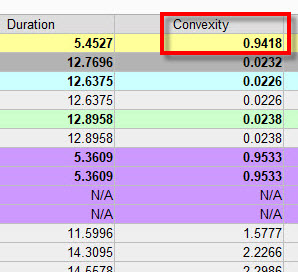
   Co bude znamenat celková Konvexnost s hodnotou 94 při objemu portfolia 1 milion korun při poklesu ceny úrokových sazeb o -1.00%?     

   Hodnota této Konvexnosti přispěje k růstu hodnoty portfolia o částku +4.700,- Kč a přidá tak tuto drobnější hodnotu k růstu ceny portfolia způsobené díky jeho Duraci.

DV01

   Dluhopisovému obchodníkovi se nabízí značné množství ukazatelů, kterými může měřit své dluhopisové investice a tyto mohou být více či méně srozumitelné. Přestože jsem se již zabýval například aktuálním výnosem, výnosem do splatnosti, Macaulayvou durací, Modifikovanou durací a nyní také Konvexností, může se nakonec zdát, že tyto pojmy neposkytují dluhopisovému obchodníkovi výrazně konkrétní přehled o tom, co mu dluhopisová investice může přinést nebo způsobit. „Když něčemu nerozumíš, přepočítej to na peníze“ je rada, kterou jsem dostal v raném mládí a je pro mě jednou z nejskvělejších myšlenek, kterou jsem mohl do své výbavy obdržet. Porozumění složitějších souvislostí při obchodování opčních kontraktů jsem často získával právě jejich přepočítáváním na to, kolik peněz obdržím a nakonec musím vydat, abych se dobral nějakého konkrétního výsledku a tyto přepočítávající operace jsem velmi často (připouštím, že někdy únavně) přenášel také na stránky tohoto webu. Kolik peněz představuje toto a kolik prostředků znamená tamto je často jediná cesta, jak pochopit i zdánlivě jednoduchou obchodní kombinaci nebo složitěji strukturovaný obchod. Nákup dluhopisu mi sice umožňuje pomocí ukazatele YTM kvantifikovat, jaký budu mít výnos do splatnosti, ale tento obdržím pouze když budu nejméně za tento výnos reinvestovat kupóny, a ještě za předpokladu, že emise nebude předčasně svolána. Durace dluhopisu mi určuje, jaký cenový pohyb na dluhopisu nastane, pokud se změní úrokové sazby, musím ale vzít v potaz zakřivení cenové křivky dluhopisu, takže tento údaj je také s „nějakou podmínkou“, jednoduše nic není zcela jasně dané a vše má nějaká svá „ale“. K dokreslení obrázku o tom, co může dluhopis umět, je zjištění jeho DV01, tedy dalšího parametru, který mohu vhodně připojit k Výnosu do splatnosti, Duraci a Konvexitě.

   DV01 je „Dolarová hodnota jednoho bazického bodu“ a jednoduše mi zobrazuje, o kolik se změní dolarová hodnota mého kupónového dluhopisu, pokud se úroková sazba změní o jeden bazický bod. Na dluhopisových trzích a trzích úrokových sazeb většinou neprobíhají významné propady a růsty o jednotky procent denně, ale v drtivé většině času se jedná o pohyby v drobných zlomcích procentního bodu. Pohyb úrokových sazeb o jedno procento znamená pohyb o 100 bazických bodů, takže například pokles z hodnoty 3.75% na hodnotu 3,64% znamená pokles o -11 bazických bodů. Mohlo by mě pak zajímat, jak se takový pohyb na úrokových sazbách promítne do změny hodnoty mého kupónového dluhopisu, a to na snadno srozumitelné dolarové bázi. Budu jednoduše chtít zjistit, kolik dolarů mi tento pohyb úrokových sazeb přinese do mého portfolia. Nebudou mě nyní zajímat procenta (jako u durace), ale konkrétní peněžní částky, které bych měl vidět na svém účtu.

   Na obrázku níže je cenový průběh mého dluhopisu z tohoto článku, tedy kupónového dluhopisu s CUSIP 91282CHZ7 se splatností 30.9.2030 a kupónem 4.625% p.a., za období od 2.1.2024 do 29.2.2024. Tento dvouměsíční průběh je porovnán s vývojem pětiletých výnosů za stejné období:

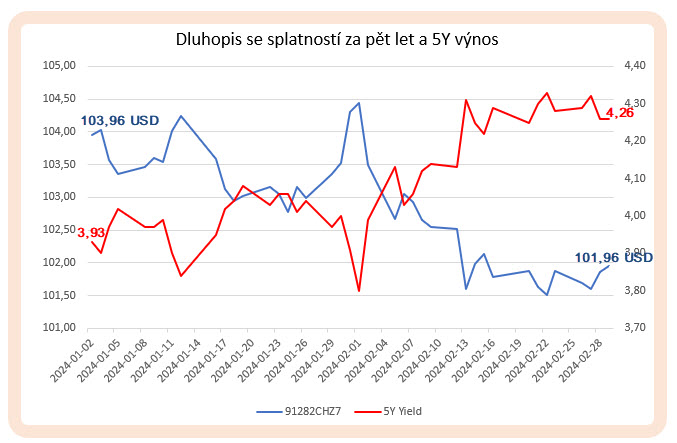
  Mohu nyní vypozorovat, že pokud bych do dluhopisu investoval 2.1.2024 částku 103,96 USD, tak ke konci února (za dva měsíce) dne 29.2.2024 by můj dluhopis stál 101.96 USD. Na tomto kupónovém dluhopisu bych tak prodělal (101.96 USD – 103.96 USD) přesně -2.00 USD. Mohu vypozorovat, že tato ztráta se přihodila za situace, kdy 2.1.2024 (při vstupu do dluhopisu) byly pětileté úrokové sazby na úrovni 3.93%, aby na konci února dne 29.2.2024 vykazovaly úroveň 4.26%, úrokové sazby za toto období tak stouply o (4.26% – 3.93%) o +0,33%, tedy o +33 bazických bodů. Mohu tak nyní konstatovat, že (-2.00 USD/33 = -0.060 USD) každý růst úrokové sazby o jeden bazický bod přineslo ztrátu -0.060 USD, tedy 6 centů na jeden bazický bod a vypočítal jsem hodnotu DV01, která činí 0.060 USD. Mohu pak konstatovat, že pokud bych investoval do tohoto dluhopisu 100 000,- USD, tak každý pohyb o +/- jeden bazický bod bude představovat cenový pohyb +/-60 USD. Tomuto dolarovému vyjádření pohybu ceny dluhopisů rozumí každý, navíc nemusím nic složitě počítat, ale mohu si nechat tuto hodnotu DV01 zobrazit v platformě TWS mého brokera Interactive Brokers:

   Zobrazovaná hodnota DV01 ve výši 0,0593 USD je téměř totožná s empiricky vypočítanou hodnotou 0.060 USD podle praktické ukázky výše. Pro praktické potřeby dluhopisového obchodníka, který by se orientoval na tento parametr, pak postačí rychlý pohled do obchodní platformy na tuto hodnotu a může citlivost změny dluhopisové investice na změnu úrokových sazeb také pozorovat pomocí této srozumitelné dolarové hodnoty.

   Mohu také k výpočtu DV01 připojit zjištění o Konvexnosti a Duraci z předchozích odstavců, kdy bylo konstatováno, že velmi malý pohyb na úrokových sazbách ovlivňuje hodnota Konvexnosti velmi nepatrně (je až druhou derivací cenové funkce dluhopisu). Pohyb o jeden bazický bod je pak opravdu velmi nepatrným pohybem, proto mohu změnu ceny dluhopisu měřit čistě hodnotou Durace, kterou nebude hodnota Konvexity zkreslovat. Mohu pak odvodit hodnotu DV01 z hodnoty Modifikované Durace z platformy TWS:

   Při aktuální ceně dluhopisu a zamýšlené investici ve výši 103.04493 USD bych při Duraci na pozorované úrovni v platformě 5.65% mohl konstatovat, že při zanedbatelném vlivu Konvexnosti by hodnota DV01 mohla být (103.04493*0,0565)*0,01 (jeden bazický bod) ve výši 0,05822 USD, tedy opět necelých šest centů, stejně jako při výpočtu výše nebo při pohledu do obchodní platformy.

  Mohu pak využít sumarizaci hodnoty DV01 na celé dluhopisové portfolio a odhadovat dopad tohoto parametru na jeho celkovou cenu. Na obrázku je opět pohled na dluhopisové portfolio prostřednictvím aplikace Risk Navigator platformy TWS brokera Interactive Brokers.

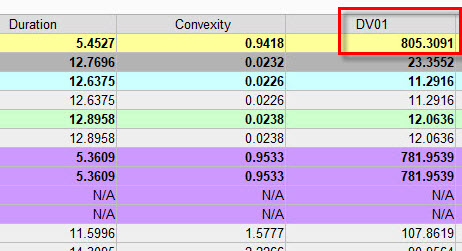
   Z obrázku mohu vypozorovat, že pro toto portfolio (Base Currency je v CZK) mám celkový údaj DV01 na úrovni 805,3091 CZK. Každým pohybem o jeden bazický bod (+/-0.01%) mé dluhopisové portfolio připíše nebo ztratí částku +/-805 CZK.

   Přestože mám k dispozici při pozorování parametrů jednotlivých dluhopisů nejrůznější údaje a metriky (YTD, Durace atd.) je pro mě hodnota DV01 nejsrozumitelnějším ukazatelem, jak se může hodnota mé dluhopisové investice vyvíjet v nejbližším časovém horizontu v tom nejjednodušším vyjádření – úbytkem nebo přírůstkem konkrétní peněžní sumy.

DV01 a Dluhopisové futures

   Pokusím se nyní vylepšit pohled na obchod z minulého článku Dluhopisy – XV. optikou výše uvedených zjištěních o dalších vlastnostech dluhopisů a jejich citlivosti na změnu úrokových sazeb. V tomto článku jsem popisoval téměř jednoměsíční držení stotisícového kupónového dluhopisu s cílem získat odpovídající kupónový výnos za toto období s tím, že pohyb úrokových sazeb a vyvolaný cenový pohyb na tomto dluhopisu jsem kompenzoval shortováním odpovídajícího dluhopisového futures. Zjistil jsem, že shortované dluhopisové futures při růstu úrokových sazeb vydělalo více, než byla ztráta na pořízeném dluhopisu a společně s přijatým kupónem to vypadalo na dobrý obchod. Bylo ale také jasné, že v případě opačného vývoje úrokových sazeb by obchod dopadl patrně tak, že dluhopisové futures by prodělalo více, než by byl zisk na nakoupených dluhopisech a společně s přijatým kupónem by obchod mohl zakončit také mírnou ztrátou. Podotkl jsem v závěru, že jsem se nezabýval dalšími vlastnostmi obou pořízených investičních nástrojů, abych mohl případně obchod vylepšit, o toto bych se mohl po získání dalších poznatků pokusit nyní.  

    Tak, jako již nyní docela přesně mohu zjistit, o kolik se změní cena kupónového dluhopisu, pokud se změní tržní úrokové sazby o jeden bazický bod (DV01), mohu stejné zjištění také aplikovat na dluhopisové futures, které hodlám použít do svého obchodu jako zajištění nakupovaného dluhopisu. Pokud jsem do obchodu z předchozího článku dluhopisového seriálu využil ZNH4, tedy březnové dluhopisové futures, u tohoto investičního nástroje opět zůstanu, protože můj obchod se bude odehrávat v období leden – únor 2024, kdy březnové dluhopisové futures je nejbližším futures kontraktem pro desetileté dluhopisy. Ve svém modelovém obchodu tak půjde opět o pořízení stotisícového kupónového dluhopisu s CUSIP 91282CHZ7 se splatností 30.9.2030 s kupónem 4.625% p.a. v první obchodní den v tomto roce (2.1.2024) a jeho prodej v poslední únorový den (29.2.2024). Jedná se tak o stejný dluhopis, kterým se zabývám v tomto článku, kde základním motivem obchodu bude zisk dvouměsíčního kupónu s tím, že se jej budu snažit zajistit tak, aby vlivem změny tržních úrokových sazeb neutrpěla cena mého dluhopisu. K nakoupenému dluhopisu tak budu opět shortovat březnové dluhopisové futures, které by mělo tuto cenovou změnu kompenzovat. Z textu tohoto článku již vím, například z údajů z mé platformy, že DV01 mého dluhopisu je 0.0593 USD na každých 100 USD investice do dluhopisu, v případě stotisícové investice tak toto bude znamenat +/-59.30 USD pohybu při změně úrokových sazeb o jeden bazický bod. V případě březnového dluhopisového futures, které bude sloužit jako stotisícové hedge k nakoupenému dluhopisu ale tento údaj k dispozici nemám a v obchodu z minulého článku jsem jej také nijak nezapojil, je totiž zcela jisté, že dluhopisové futures reaguje na změnu úrokových sazeb s nějakou citlivostí a toto bych mohl při konstrukci obchodu využít. Mám dvě možnosti, jak toto zjistit. Mohu získat data o úrokových sazbách za minulé období a stejná data o vývoji ceny dluhopisového futures a z poměru změny ceny dluhopisového futures a změny úrokových sazeb pak odvodit, jaká dolarová hodnota dluhopisového futures odpovídá změně pohybu úrokových sazeb o jeden bazický bod a stanovit tak hodnotu DV01 pro dluhopisové futures. Hodnotu DV01 kupovaného dluhopisu pak bude stačit poměřit s hodnotou DV01 dluhopisového futures a z tohoto poměru bych pak mohl odvodit, jaký má každý z investičních nástrojů výkon ve vztahu ke změně úrokových sazeb o jeden bazický bod a tomuto přizpůsobit konstrukci obchodu. Zjišťování DV01 dluhopisového futures takovým postupem by ale bylo nepraktické, možná také pracné a mohlo by být navíc nepřesné. Mohu ale využít poznatků načerpaných na tomto webu a přistoupit ke zjištění DV01 dluhopisového futures sofistikovaněji.

   V článku Dluhopisy – XIV. jsem popisoval způsob, jak jsou dluhopisová futures u své expirace vypořádávány s tím, že jako investorovi do těchto dluhopisových derivátů se mi nepřihodí, že budu něco nějakým způsobem vypořádávat, protože je snažší se dluhopisového futures zbavit na volném trhu, který je mimořádně likvidní, navíc můj broker ani takovou možnost fyzického vypořádání nepřipouští. Nicméně jsem se v článku zabýval procedurou takového vypořádání zejména se záměrem zjistit, co je podkladovým aktivem dluhopisového futures a jaký vypořádávaný dluhopis vlastně toto futures kopíruje. Zjištěním bylo, že k vypořádání není určen jediný dluhopis, ale celý koš těchto dluhopisů, které se volně obchodují na trhu a každý z těchto dluhopisů pak mohu, jako držitel dluhopisového futures, vybrat k dodání při vypořádání. Zjištění dále obsahovalo, že každý z těchto možných dodávaných dluhopisů má jiné vlastnosti (kupón, cenu a dobu do splatnosti), takže cena vybraného dodávané dluhopisu z možného koše bude upravena při vypořádání koeficientem s názvem Conversion Factor tak, aby odpovídala parametrům ideálního dluhopisu, který je popsán v prospektu dluhopisového futures. Dluhopisové futures tak kopíruje každý dluhopis z možného koše dodávaných dluhopisů, rozmanitost těchto dluhopisů pak při vypořádání do představy o předpisovém dluhopisu zajišťuje právě tento Conversion Factor.

   Přesunu se nyní na webové stránky burzy CME do sekce Treasury Analytics, abych mohl zjistit hodnotu DV01 pro dluhopisové futures jednodušeji, rychleji a pravděpodobně také přesněji:

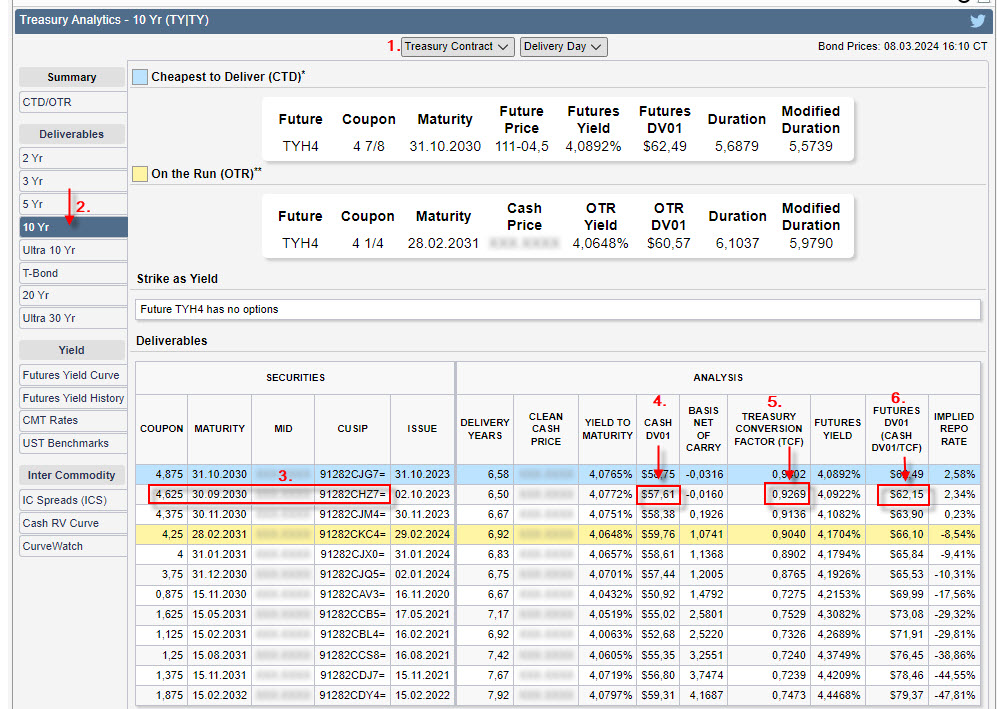
   V hlavním menu (1) zvolím požadovaný březnový kontrakt a z březnových kontraktů mě bude zajímat obsah koše možných dodávaných dluhopisů (Delivery Basket) pro desetileté dluhopisové futures ZNH4 (2). Mohu vypozorovat, že mnou použitý kupónový dluhopis s CUSIP 91282CHZ7 se splatností 30.9.2030 s kupónem 4.625% p.a. (3) je součástí tohoto koše a je tak předurčen k případnému dodání při vypořádání. Mohu také zjistit, že DV01 tohoto dluhopisu je 57,61 USD (4), tedy pohyb na stotisícovém dluhopisu odpovídá zjištění z mé obchodní platformy o tom, že pohyb o jeden bazický bod bude představovat změnu mé investice o +/- 57.61 USD. Pokud bych chtěl tento dluhopis označit jako dodávaný k vypořádání, musel bych počítat s tím, že namísto vypořádávaného dluhopisového futures se mi po proceduře settlement objeví na účtu tento dluhopis, jehož dodávaná cena ale bude upravena příslušným koeficientem Conversion Factor aktuálně na hodnotě 0,9269 (5). Nezískal bych tak plnou hodnotu aktuální ceny tohoto dodávaného dluhopisu, ale jeho upravenou cenu tak, aby dodání tohoto dluhopisu nebylo pro mě výhodnější, než v případě dodání jiné dluhopisové emise. Protože tato úprava o Conversion Factor srovnává do řady všechny možné dodávané dluhopisy na úroveň ideálního dodávaného dluhopisu, které toto dluhopisové futures kopíruje, mohu lehce odvodit, že podíl dluhopisového DV01 a hodnoty Conversion Factor tohoto mého dluhopisu vygeneruje DV01 vypořádávaného dluhopisového futures. Podíl DV01 mého dluhopisu s CUSIP 91282CHZ7 s hodnotou 57,61 USD a jeho Conversion Factor 0,9269 mi pak opravdu určí (57,61/0,9269) hodnotu DV01 březnového dluhopisového futures ZNH4 na hodnotě 62.15 USD (6).

    Mohu tak konstatovat jednoduché, pokud se změní úrokové sazby o jeden bazický bod, změní se cena mého stotisícového dluhopisu o +/- 57.61 USD, zatímco stejný pohyb o jeden bazický bod u dluhopisového futures ZNH4 bude představovat cenový pohyb +/-62.15 USD. Z tohoto nepoměru pak bude vyplývat, že dluhopisové futures bude na změny úrokových sazeb reagovat citlivěji a s větší volatilitou, než tomu bude u nakoupeného dluhopisu.

    2.1.2024 nakupuji kupónový dluhopis s CUSIP 91282CHZ7 se splatností 30.9.2030 s kupónem 4.625% p.a., který stojí 103,96% Face Value, tato investice bude s výdajem -103 960 USD. Ve stejný den shortuji ZNH4, desetileté dluhopisové futures, které se aktuálně obchoduje za 112,30 a představuje teoretický příjem ve výši +112 300 USD (jeden bod dluhopisového futures představuje 1.000 USD). V průběhu měsíce ledna a února úrokové sazby mírně rostly, aby zaznamenaly nárůst o +30 bazických bodů (+0,30%), toto indikuje pokles hodnoty nakoupených dluhopisů a ceny dluhopisového futures. 29.2.2024, poslední únorový den, vystupuji s obchodu prodejem dluhopisů a zpětným nákupem shortovaného dluhopisového futures s výsledkem níže v obrázku:

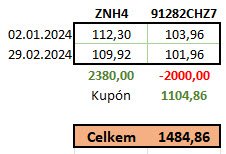
   Dluhopis prodělal při růstu úrokových sazeb přesně -2.000 USD, ale přinesl kupón za 86 kalendářních dnů ve výši +1.104,86 USD. Dluhopisové futures, které jsem shortoval, vydělalo +2.380 USD, tedy vydělalo více, než prodělala investice do dluhopisů. Celkově zakončil obchod profitem +1.484,86 USD. Toto je sice skvělé, ale vadí mi rozdíl mezi profitem dluhopisového futures a ztrátou na dluhopisech, kde rozdíl činí 380 USD. Tento bude patrně způsoben jinou výkonností každého investičního nástroje při pohybu úrokových sazeb, který jsem popsal například v parametru DV01. Mohu proto zapojit toto zjištění do stejného obchodu, ale s jinými vstupními parametry.

   DV01 dluhopisu s CUSIP 91282CHZ7 se splatností 30.9.2030 s kupónem 4.625% p.a. je na hodnotě z platformy Treasury Analytics na úrovni 57.61 USD a stejný parametr DV01 pro dluhopisové futures je 62.15 USD. Z poměru 57.61/62.15 vyplývá, že dluhopisové futures má o 7,30% větší cenový pohyb než je odpovídající cenový pohyb na dluhopisech při pohybu úrokových sazeb o jeden bazický bod. Nemohu pořídit o 7,30% méně dluhopisového futures, ale mohu pořídit o +7.30% více dluhopisů, abych tento rozdíl vyrovnal a dosáhl tak stejného vlivu DV01 při pohybu úrokových sazeb o jeden bazický bod. Musím se pokusit zařídit, aby tento pohyb úrokových sazeb o jeden bazický bod měl podle parametru DV01 stejný účinek na obě části obchodu. Pokud bych nakoupil o +7.30% dluhopisů více, mohl bych pozorovat, jak se obchod vyvinul v tomto cenovém rozložení:

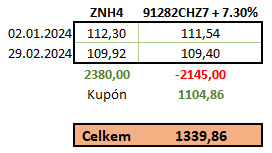
   Výsledek obchodu s navýšenou investicí do dluhopisů o +7.30% přinesl vyšší ztrátu na dluhopisové části obchodu, toto samozřejmě vedlo ke zhoršení výsledku celkového obchodu, protože investice do zajišťujícího futures byla se stejným výsledkem, nicméně rozdíl mezi ziskem na dluhopisovém futures a dluhopisech se snížil z původního rozdílu 380 USD na rozdíl ve výši (380-145) ve výši 235 USD. Mohu tak předpokládat, že takto upravený obchod by vedl k přesnějšímu poměru investice a jejího zajištění a při opačném průběhu vývoje úrokových sazeb (nikoliv růst, ale jejich pokles) za dobu trvání obchodu by mohl přinést uspokojivější výsledek. S ohledem na to, že do budoucnosti nevidím, by takto upravený obchod byl pravděpodobně přijatelnější a klidnější variantou namísto investice do obou části obchodu se stejnou dolarovou hodnotou

   Poznání dalších parametrů spojených s dluhopisy může přinést další benefity při rozhodování, jak mám na svou případnou investici do dluhových cenných papírů nahlížet a co od ní mohu v budoucnosti očekávat. Mnoho parametrů vypadá složitě a nepochopitelně, zejména s ohledem na jejich výpočet, nicméně jejich interpretace není složitá a nakonec nemusím ani způsobu výpočtu rozumět, hodnotu těchto parametrů mohu pohodlně získat ze své obchodní platformy. Stačí pak mít základní povědomí, co může tento údaj znamenat a investice do dluhopisů může být pochopitelnější a smysluplnější a může splnit očekávané předpoklady, se kterými do takové investice vstupuji.

   Komentáře a příspěvky k tomuto článku prosím směrujte do Diskuzního fóra do tohoto vlákna :c)