„Ahoj, půjč mi prosím tě milion, já ti to za rok roky vrátím a k tomu přidám desetiprocentní úrok, dík“. Takto by mohla znít jednoduchá domluva na banální půjčce s kamarádem, se kterým jsem sdílel školní lavici na devítiletce a která by mohla odpíchnout téma dluhopisů na tomto webu. Je s podivem, jak roztříštěné jsou informace o dluhopisech, jejich podstatě a možnosti obchodování na českých internetových stránkách o investování, mám tedy na mysli především obchodování s dluhopisy prostřednictvím obchodních platforem zavedených brokerských společností a nikoliv nabídku tuzemských více či méně důvěryhodných podniků, které se rozhodly vydat a umístit mezi veřejností dluhopisy pro financování svých podnikatelských aktivit (toto „domácí téma“ tak ponechám zcela bez komentáře). 

   Pořízení dluhopisu je poskytnutí peněžní půjčky osobě, která jej vydala. Od této osoby pak očekávám vrácení zapůjčeného obnosu v dohodnutém okamžiku v budoucnosti a za tuto poskytnutou službu pak očekávám nějakou odměnu. Z tohoto pohledu je pak patrné, že se jedná o transakci, která pravděpodobně historicky odpovídá období vynálezu peněz, věřitel dlužníkovi předává peníze, opačným směrem pak putuje dluhopis – cenný papír, který je na svém povrchu popsán parametry této transakce, tento „pravěk“ je nyní překonán existencí dluhopisů v elektronické formě, tyto jsou také elektronicky obchodovány. Stejně tak jako peníze na nákup dluhopisu jsou v elektronické formě předisponovány od věřitele k dlužníkovi, stejně tak je elektronicky změněn v patřičných rejstřících záznam o vlastnictví dluhopisu, s dluhopisy se tak pravděpodobně v drtivé většině případů „fyzicky nepomazlíte“. Myslím, že tím jsem se „dluhopisovým dějepisem“ a povinnými reáliemi vypořádal, protože to pro další bude zcela nepodstatné. V článcích mě budou zajímat především zcela konkrétní a praktické stránky týkající se dluhopisů, jak je správně pochopit, vyhodnotit a také obchodovat. Pořízení akcie, futures nebo opčního kontraktu je doprovázeno nejistotou cenového pohybu, cena těchto investičních nástrojů může výrazně poklesnout nebo nabýt na hodnotě s ohledem na tržní podmínky, které formují jeho cenu, dluhopisy jsou však trošku „jiná kategorie“. Jejich pořízením v žádném případě nevstupuji do zcela bezrizikového prostředí, ale mohu se alespoň mírně spolehnout na jakýsi pevný výnos (fixed income), který z jeho držení vyplývá. Není to ale vůbec jednoduché pochopit všechna rizika, která s takto „pevným výnosem“ souvisejí a jestli se opravdu takto nazvaný výnos přetaví do reality se budu snažit v tomto a dalších článcích popsat.          

Budoucí hodnota investovaných peněz

   Vyhodnocení investice do dluhopisu tkví v prozkoumání a posouzení mnoha kritérií vážících se k dluhopisu, ze kterých mohu usuzovat na rizika, která z takové investice plynou. Budu se jimi podrobně zabývat později, nicméně základním a nejjednodušším požadavkem u poskytnuté půjčky by mohla být informace, kolik vlastně na této finanční transakci mohu vydělat. Jednomilonová roční půjčka kamarádovi s jednorázovým splacením za rok a s úrokem 10% by se tak mohla transformovat do otázky, jaká je budoucí hodnota dnes půjčené částky peněz? Touto, na první pohled zcela banální otázkou, se budu zabývat v tomto článku. V tomto jednoduchém příkladu to není nic složitého, protože 10% z půjčeného 1,000.000,- Kč představuje odměnu za půjčení peněz ve výši 100.000,- Kč, a pokud mi kamarád půjčený milion za rok opravdu vrátí, je budoucí hodnota nyní půjčeného milionu korun rovna částce 1,100.000,- Kč. Toto je nejjednodušší případ výpočtu budoucí hodnoty peněz, na který nepotřebuji žádnou matematickou průpravu nebo složité vzorce, je ale jisté, že ve skutečnosti bude nakládání s penězi složitější a výpočty budou značně komplikovanější. Stačí k velmi jednoduchému obchodnímu případu se zapůjčeným milionem na jeden rok přimyslet delší dobu splatnosti než je právě tento jeden rok (například tři roky) s podmínkou, že budu chtít za zapůjčené peníze opět desetiprocentní úrok splatný ke konci každého roku půjčky a k parametrům této transakce si mohu přimyslet reinvestování přijatého úroku za nějakou běžnou úrokovou sazbu (nenechám jednoduše vydělané peníze jenom tak ležet). Problém stanovení budoucí hodnoty mnou půjčených peněz se tak okamžitě rozšiřuje na další dílčí problémy a související výpočty.       

   Nechám nyní situaci s půjčkou stranou a představím si, že se svým milionem korun čelím telefonátu z mé banky, která mi nabízí zhodnocení mých peněz na tříletém termínovaném vkladu s úrokem 10% p.a. Protože „rajfajzence“ věřím více než svému spolužákovi ze základky, rozhodl jsem se, že prozkoumám, jaká bude hodnota mého jednoho milionu korun za tři roky od okamžiku otevření takto termínovaného vkladu. Mohu nyní rekapitulovat tuto nabídku tak, že nyní vložím na termínovaný účet jeden milion korun, za jeden rok (p.a.) mi banka připíše první splátku úroku 10% p.a., tedy ve výši +100.000,- Kč, tento úrok na tomto spořícím účtu ponechám a budu vyčkávat, jakou částku úroku mi připíše banka na konci druhého roku tříletého termínovaného vkladu, poté opět nebudu žádné peníze vybírat a budu vyčkávat, jaká výplata mě po třech letech této „půjčovací“ operace bude čekat.

1.rok: vklad: 1.000.000,- Kč, úrok 10% = +100.000,- Kč, konečná částka 1,100.000,- Kč

2.rok: vklad: 1.100.000,- Kč, úrok 10% = +110.000,- Kč, konečná částka 1,210.000,- Kč

3.rok: vklad: 1.210.000,- Kč, úrok 10% = +121.000,- Kč, konečná částka 1,331.000,- Kč

   Pokud by vše proběhlo jak mělo, nebyly mi sraženy žádné bankovní poplatky nebo daně za přijaté úroky, měl bych po třech letech disponovat sumou 1,331.000,- Kč, toto by pak byla budoucí hodnota mého jednoho milionu korun podle nastavených podmínek mého dlužníka, který slibuje 10% roční zhodnocení vložené částky. Nemusím být nějaký vědec, abych již na tomto jednoduchém příkladu vytušil, že vydělaná suma peněz z této transakce se bude odvíjet zejména od třech základních parametrů – 1/ délky období, na které peníze půjčuji, 2/ úroku, který je mi slíben a 3/ periodě, za kterou je mi vyplácen tento slíbený úrok. Obě transakce, tedy půjčku kamarádovi a nákup finančního produktu – termínovaného vkladu, se nyní  pokusím podrobit hlubšímu prozkoumání s nějakým mírně zmatematizovaným přístupem.     

   Nejjednodušší formule, pomocí které mohu analyzovat budoucí hodnotu mé investice a najít odpovědi na otázky, jak se změní budoucí hodnota mého milionu korun, když změním nějaký parametr transakce, je uvedena níže:

   BH je budoucí hodnota investice, SH je současná hodnota půjčovaných peněz, úrok je dohodnutá úroková sazba za dohodnuté období půjčky a n je počet období, za které bude vyplácen dohodnutý úrok. Mohu tak prozkoumat nejdříve nejjednodušší případ půjčeného milionu korun na jeden rok mému kamarádovi s odměnou za půjčení ve výši 10%.

   Při zapůjčení 1,000.000,- Kč (SH = 1.000.000), dohodnutému úroku 10% (úrok = 0.10 jako desetinné číslo) a skutečnosti, že tento úrok dostanu za rok při splátce půjčky, tedy počet období, za které dlužník zaplatí úroky je 1 (n =1), mohu výsledek – budoucí hodnotu dnes půjčené částky peněz vypočítat za použití uvedeného vzorce konkrétně takto:

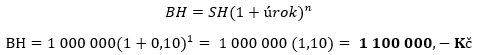
   Přestože nemusím pro tak jednoduchou výpočetní operaci výpočet vůbec zapojit, je jeho využití důkazem, že má početní operace je správná, budoucí hodnota půjčeného jednoho milionu korun je opravdu 1,100.000,- Kč. Mohu nyní takto jednoduše formulovanou investici do jednoroční půjčky mému kamarádovi zkomplikovat a vyhodnotit tři možné varianty, které by mohly reálně nastat. Nejdříve vyhodnotím, jaká by byla hodnota mé investice, kdyby se před splátkou půjčky můj kamarád ozval s tím, že půjčku splatí o měsíc později a bude respektovat, že zaplatí „nějaké úroky navíc“. Při zachování férovosti a dohodnutém úroku 10% p.a. bych mohl uvažovat tak, že nebudu chtít 10% úrok za 365 dnů, ale za 365 + 30 dnů, tedy za 395 dnů (červená šipka ve vzorci níže), což odráží třicetidenní zpoždění se splátkou dohodnuté půjčky za zachování dohodnutých úrokových pravidel, výpočet by pak vypadal následovně:   

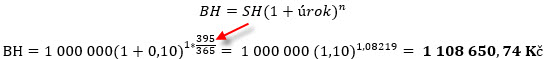
   Měsíční zpoždění se splacením poskytnuté půjčky by mi pak přineslo, kromě splátky jistiny půjčky a ročního úroku +100.000,- Kč, další úroky ve výši +8.650,74 Kč. Stejnou logiku by pak mělo předčasné splacení půjčky ve lhůtě kratší než zamýšlený jeden rok, například po 210 kalendářních dnech (sedm měsíců).

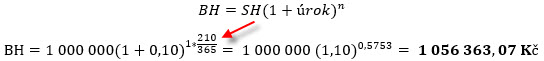
   Předčasné splacení milionové půjčky po sedmi měsících od jejího poskytnutí by mě opravňovalo požadovat po dlužníkovi úrok pouze ve výši +56.363,07 Kč při domluvené sazbě 10% p.a.

   Ve třetí variantě bych pak mohl prozkoumat, kdyby po 210 kalendářních dnech (sedmi měsících) mi byla vrácena polovina půjčených peněz ve výši 500.000,- Kč a zbylý doplatek půjčky ve výši 500.000,- Kč byl vrácen v dohodnutém termínu za jeden rok i s dohodnutými úroky ve výši 10% p.a., jakou částku bych mohl u splatnosti půjčky očekávat?

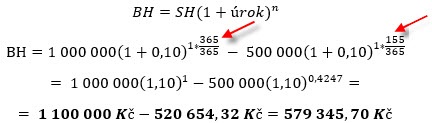
   Po splacení poloviny peněz jistiny půjčky po sedmi měsících trvání půjčky bych mohl očekávat u splatnosti druhé poloviny půjčky částku 579.345,70 Kč. Tato je vypočtena jako hodnota původní půjčky s dohodnutým ročním úrokem 10% p.a., od které odečítám tu část roku, kdy mi neběží úrok z celé částky půjčky, ale pouze z její zbylé poloviny (365 dnů – 210 dnů = 155 dnů). Mohu tak vypozorovat, že předčasným splacením části půjčky dlužník nemusel zaplatit úroky ve výši +100.000,- Kč, ale pouze +79.345,70 Kč.

   Pro takto jednoduchou transakci s jednoroční půjčkou jsem se však nerozhodl a mou volbou bylo nakoupení finančního produktu – uzavření tříletého termínovaného vkladu v mé bance s připisováním 10% úroku pro každý rok jeho trvání. Tuto operaci pak mohu aplikovat na daný vzorec a sledovat, jestli se výpočet shoduje s popisem tříletého období, jak bylo rozebráno výše v článku se stanovenou budoucí hodnotou investovaných peněz ve výši 1,331.000,- Kč. Tedy, při uzavření termínovaného vkladu pro částku 1,000.000,- Kč (SH), dohodnutému úroku 10% p.a. (úrok = 0,10 jako desetinné číslo) a skutečnosti, že tento úrok dostanu na konci každého roku trvání vkladu, tedy počet období, ze které mi banka poskytne dohodnutý úrok je 3 (n), mohu výsledek – budoucí hodnotu dnes investované jednomilionové částky do termínovaného vkladu vypočítat za použití výše uvedeného vzorce konkrétně takto:

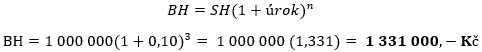
   Pozoruji, že jsem opravdu dostal výpočtem stejnou budoucí hodnotu investovaných peněz jako v rozebraném případě po jednotlivých rocích v článku výše.

   Protože jsem z termínovaného vkladu nic nevybíral a ponechal připsaný roční úrok k dalšímu zhodnocování v dalších letech, vynesla mi investice do tříletého termínovaného vkladu více než pokud bych třikrát za sebou půjčil svému kamarádovi na jeden rok jeden milion korun s 10% úrokem u splatnosti této jednoroční půjčky. Bude proto nyní určitě důležité k zapamatování, že pokud budu držet dluhopis s kupónem a tento kupón bude v nějakých časových intervalech emitentem placen, nebude parně prozíravé inkasovanou kupónovou platbu utratit, ale zhodnocovat ji společně s investicí do ceny dluhopisu.

   Avizoval jsem, že pro míru zhodnocení vložených peněz do termínovaného vkladu bude hrát roli délka zvoleného časového období držení této investice, výše dohodnutých úroků a frekvence jejich připisování. Na obrázku níže je ukázka, jak by se zhodnocoval investovaný jeden milion korun za období nikoliv tří let, ale ponechal bych jej pracovat deset let.

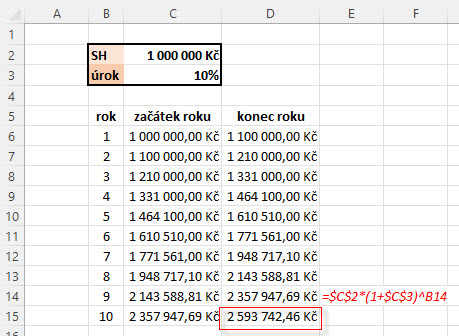
   Z obrázku vyplývá, že na konci desetiletého období bych investici 1,000.000,- Kč přetavil do konečné částky 2,593.742,46 Kč, což by nebylo vůbec špatné, protože takto nastavené úročení by přineslo více než jeden a půl milionu korun k původně vložené částce. Na obrázku jsem rovněž (pro jistotu) ukázal vzorec výpočtu pro devátý rok investice, jak si jej mohu vytvořit v excelu. To, že růst hodnoty investice není lineární pramení z podstaty výpočtu a mohu si jej vynést do jednoduchého grafu.

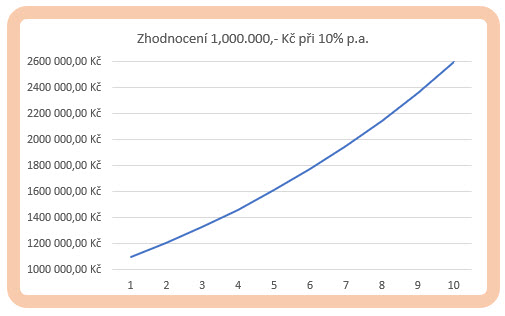
   Čím déle budu držet takto nastavenou investici, tím více vydělám, to je z výpočtu patrné. Mohu si pak stejně logicky odvodit, že růst úrokové sazby (nebo její pokles) bude mít na celkovou investici přímý vliv. Růst úroků o +2% na úroveň 12% p.a. při sjednávání termínovaného vkladu by přinesla tento výsledek

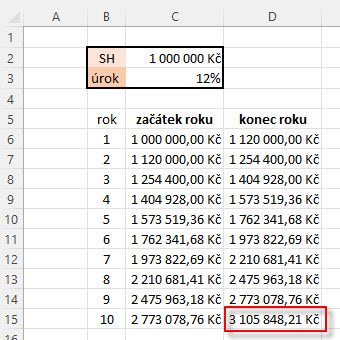
   Navýšení úroků o dva procentní body by přispělo ke zhodnocení jednoho milionu korun za deset let při úrokové sazbě 12% s roční frekvencí připisování úroků na částku 3,105.848,21 Kč. Mohu pak prozkoumat stejný výpočet se snížením úrokové sazby, například o -3% na úroveň 7% p.a. při sjednání stejné desetileté investice.

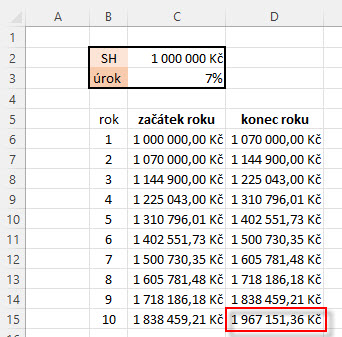
   Nižší hladina dohodnutých jednoročních úroků ve výši 7% p.a. by pak způsobila, že po deseti letech trvání termínovaného vkladu s počátečním vkladem jeden milion korun by konečná částka činila 1,967.151,36 Kč.

   Zajímavé by však bylo, zejména z pohledu zvoleného tématu dluhopisů, pokud by časově omezená investice změnila frekvenci připisování úroků. Mohl bych tak nyní po mé jednomilionové investici chtít, aby frekvence připisování úroků nebyla jedenkrát za rok (p.a.), ale připisování by se provádělo každého půl roku (semi-annual). Mírně předběhnu téma, na obrázku níže je výňatek z popisu amerického vládního dluhopisu se stejnou frekvencí platby přislíbeného úroku (kupónu).

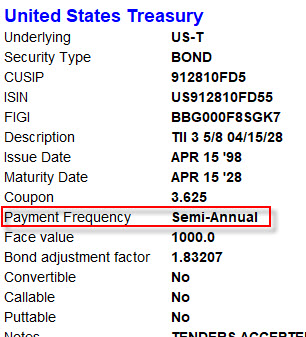
   Musím tak svůj výpočet budoucí hodnoty peněz vložených například do desetiletého termínovaného vkladu s připisováním úroků 10% p.a. každého půl roku přizpůsobit pro použití vzorce výpočtu jako v předcházejících případech. Současná hodnota (SH) bude stále 1,000.000,- Kč, hodnota pro úrok bude představovat částku 10% p.a./2, tedy 5% (do vzorce úrok = 0.05) za dohodnutou periodu připisování (pololetí) a počet period (n) bude 20 a představuje počet pololetí, které obsahuje sjednaná doba pořízení investice, dohodnutých deset let je tvořeno 20-ti pololetími.

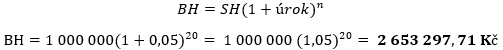
   Vypočítávám, že pokud bych pro vstupní investici jeden milion korun měl sjednáno pololetní připisování úroků za sjednané sazby 10% p.a., vyneslo by mi její desetileté držení částku 2,653.297,71 Kč namísto stejně trvající investici se stejným úrokem, ovšem s připisováním stejných úroků pouze jednou za rok, toto by dosáhlo konečné částky 2,593.742,46 Kč (viz výše v textu), rozdíl by tak činil zhruba -60.000,- Kč v neprospěch jednoročního připisování úroků. Budoucí hodnota peněz vložených do těchto dvou podobných investic by pak byla vyšší u té z nich, která by při stejných parametrech částky, délky trvání a stejného úroku nabízela vyšší frekvenci připisování úroků. Mohl bych toto obecně přičítat vyšší šanci na reinvestování přijatých úroků u investice s častějším připisováním úroků.            

   Termínované vklady mě však zajímat nebudou, i když je jeho pořízení dobrou teoretickou průpravou, jak nahlížet na investici s pevně stanoveným příjmem. Nákup dluhopisu je ale podobnou investicí, vykazuje však zjevnou zásadní odlišnost – reinvestování přijatých peněz z kupónových výplat nebude nic automatického jako u připisování úroků na termínovaném vkladu, ale bude záležet vyloženě na příjemci, jak s takovými kupónovými příjmy naloží. V reálném světě se pak může stát, že pořídím investiční nástroj (dluhopis) na který vydám 1,000.000,- Kč se splatností za deset let a s pevným úrokem ve výši 7% p.a. (kupónem) vypláceným jedenkrát za rok (vždy na konci roku), nicméně peníze z kupónových výplat mi budou zasílány na obchodní účet, který je úročen částkou pouze 2% p.a., tedy výrazně jinou úrokovou sazbou, než je úročena má dluhopisová investice. Výpočet očekávané budoucí hodnoty mé investice jeden milion korun do dluhopisu, pokud se rozhodnu držet jej až do doby jeho splatnosti za deset let, pak bude sestávat ze tří součástí – A/ nominální hodnoty dluhopisu při jeho splatnosti (1,000.000,- Kč), B/ inkasovanému příjmu za všechny kupóny (7% z 1,000.000,- Kč = 70.000,- Kč x 10 let = 700.000,- Kč) a C/ příjmu z úroku, který získám úročením přijatých kuponových plateb sazbou 2% p.a. na mém běžném obchodním účtu – toto musím nyní vypočítat.      

   Provést tento výpočet znamená zahrnout do něj skutečnost, že pokud koupím dluhopis za 1,000.000,- Kč s kupónem 7% p.a. vypláceným jednou ročně (modelově investuji 1.1.2022 a kupón 70.000,- Kč se vyplácí poprvé 31.12.2022), musím čekat celý jeden rok na první splátku kupónu. Úročení tohoto kupónu úrokem 2% p.a. na mém obchodním účtu tedy začíná až od prvního dne druhého roku mé investice. K takovému výpočtu využiji níže uvedený vzorec, který mi říká, jaké bude zhodnocení přijatých kupónů na konci mé investice, tedy po uplynutí n – období, za kterých je tento kupón vyplácen:

   Jak tedy bude vypadat výpočet úročení 2 % p.a. v první rok investice, kdy na jeho konci obdržím kupón ve výši 70.000,- Kč a počet uběhlých let bude jedna (n = 1)? Hodnota vypočítaná podle vzorce za tento první rok bude muset odpovídat pouze hodnotě přijatého kupónu (70.000,- Kč), protože žádné úroky požadovat nemůžu.

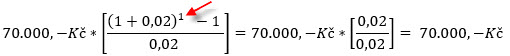
  Na konci druhého roku, kdy budu mít k dispozici již 140.000,- Kč a z toho prvních 70.000,- Kč mám již úročeno 2% p.a., by pak výpočet podle vzorce vypadal následovně:

   Na svém běžném účtu bych pak již mohl vypozorovat, že po dvou letech držení dluhopisu jsem jeho přijatý kupón ve výši 140.000,- Kč zhodnotil o (141.400,- Kč – 140.000,- Kč) částku +1.400,- Kč. Mohu proto na nyní mé desetileté držení (n=10) jednomilionového dluhopisu s ročním kupónem 7% p.a. (70.000,- Kč) a úročením přijatého ročního kupónu ve výši 2% p.a. (r = 0,02) na mém běžném obchodním účtu nasadit výše uvedený vzorec a vypočítat příjem z úročených kupónů takto:

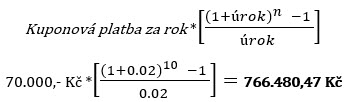
   Protože jsem na svůj účet za deset let přijal kupónové platby v nominální výši 700.000,- Kč (10*70.000,- Kč) je můj čistý úrokový výnos z reinvestice přijatých kupónů na mém účtu sazbou 2% p.a. (766.480,47 Kč – 700.000,- Kč) ve výši +66.480,47 Kč.

   Mohu tak konstatovat, že jsem po deseti letech obdržel zpět 1,000.000,- Kč + kupóny ve výši +700.000,- Kč + úrok z reinvestice kupónů ve výši +66.480,47 Kč a budoucí hodnota mé investice do takto strukturovaného dluhopisu za popsaných podmínek by se tak rovnala částce 1,766,480,47 Kč.

   Americké vládní dluhopisy nebo korporátní dluhopisy nejběžněji vyplácejí kupón každého půl roku (např. obrázek s charakteristikou T-bondu v textu výše), pokud bych tedy takto investoval jako výše do desetiletého dluhopisu jeden milion korun, kupónová platby 7% p.a. by byla vyplácena pololetně (v mém modelovém příkladu poprvé za půl roku od pořízení dluhopisu) a nakonec by můj běžný účet byl stále úročen sazbou 2% p.a., musel bych parametry výpočtu pro reinvestování upravit. Počet termínů, kdy bude kupón vyplácen by byl dvojnásobný (deset let představuje dvacet pololetí), proto n = 20. Neobdržel bych jednou ročně 70.000,- Kč jako roční kupón 7% p.a. z držení dluhopisu, ale každého půl roku bych inkasoval jeho polovinu ve výši 35.000,- Kč, stejně tak bych musel redukovat úrokovou sazbu pro reinvestici přijatých kupónových plateb na polovinu (2% p.a./2), proto úrok = 0.01. Výnos z reinvestice přijatých kupónů by pak byl:

   Opět jsem na svůj běžný obchodní účet za deset let přijal kupónové platby 700.000,- Kč (10*70.000,- Kč), ale změnou frekvence kupónových výplat z deseti na dvacet (z roční na pololetní) je můj čistý úrokový výnos z reinvestice přijatých kupónů na mém účtu sazbou 2% p.a. (770.665,14 Kč – 700.000,- Kč) vy výši +70.665,14 Kč (obdržel bych o +4.184,67 Kč více).

   Mohu tak opět konstatovat, že jsem po deseti letech obdržel zpět 1,000.000,- Kč + kupóny ve výši +700.000,- Kč + úrok z reinvestice kupónů ve výši +70.665,14 Kč a budoucí hodnota mé investice do takto strukturovaného dluhopisu za popsaných podmínek by se tak rovnala částce 1,770,665,14 Kč. Je tak patrné, že zvýšení frekvence připisování úroků měla vliv také na reinvestici přijatých kupónů.

    Zjištění budoucí hodnoty investovaných peněz je základní premisou pro pochopení, jaká je jejich cena a jak mohu na investované peníze nahlížet, pokud jsem se rozhodl pro investici s pevně daným příjmem – dohodnutými úroky nebo vyznačeným kupónem a nakonec jsem se také rozhodl, že přijatý úrokový výnos neutratím, ale budu jej nějakým způsobem reinvestovat. Mohl by mě ale zajímat také opačný pohled na zamýšlenou investici, a to chtít znát současnou hodnotu mé investice, pokud budu chtít vydělat nějakou předem stanovenou sumu v budoucnosti investicí do investičního nástroje s takto pevně daným příjmem, a to opět například ve formě vyznačeného kupónu nebo jakkoliv jinak definovaného slíbeného procentního zhodnocení. Jak zjistím, kolik musím nyní investovat, abych na svém účtu viděl za pět let částku 2,223.186 Kč při investici do dluhopisu s kupónem 8.50% p.a., který se vyplácí jednou za půl roku? O tom v příštím článku…:c)

  Komentáře a příspěvky k tomuto článku prosím směrujte do Diskuzního fóra do tohoto vlákna :c)