Zjistit, jaká je budoucí hodnota investovaných peněz za určitých úrokových podmínek, bylo popsáno v minulém článku. Pořídit investici s pevným příjmem v budoucnosti představovalo nasazení jednoduchých početních úkonů, abych se dobral výsledku, který reprezentoval představu o budoucí hodnotě investice, její výše byla zejména podmíněna délkou držení investice, výši přijatého plnění z dohodnutého úroku, frekvenci s jakou jsou tyto odměny za poskytnutou investici vypláceny a nakonec také rozhodnutí, jestli se postupně přijímané úrokové platby rozhodnu reinvestovat, celkový součet těchto budoucích peněžních toků pak zobrazil budoucí hodnotu celé realizované investice. Předmětem tohoto článku bude ale řešení zcela opačného problému, budu se snažit zjistit, jakou sumu mám dnes investovat, abych za přesně daných podmínek této investice mohl utržit přesně danou hodnotu investice v budoucnosti. V příměru s jednoroční jednomilionovou půjčkou mému kamarádovi s 10% úrokem při její splatnosti jsem v minulém článku hledal odpověď, jaká bude hodnota mé investice za rok. Velmi jednoduchým výpočtem jsem zjistil, že budoucí hodnota je 1,100.000,- Kč. Nyní ale budu řešit opačný problém, tedy hledat, jaká má být přesně aktuální výše mé investice, abych při požadovaných podmínkách půjčky docílil částku 1,100.000,- Kč.    

Současná hodnota investovaných peněz

   Vzorec pro výpočet budoucí hodnoty investovaných peněz v minulém článku měl tento tvar:

   BH je označení budoucí hodnoty investice, SH je výraz pro současnou hodnotu investovaných peněz, úrok je desetinné číslo představující úrokovou sazbu za sjednané období investice a n je výraz pro počet období, za které se vyplácí sjednaná úroková sazba. V jednoduché algebraické úpravě tohoto vzorce pak mohu pro hledanou současnou hodnotu investovaných peněz SH nalézt tuto jednoduchou interpretaci:  

   Tento vzorec pak bude předmětem zkoumání v tomto článku a bude představovat výpočet, jaká by byla hodnota současná investice (SH), abych při předpokládaném počtu period vyplácejících úrok (n) pro zadané, předpokládané nebo požadované úrokové sazbě (úrok) pro zadanou periodu, utržil požadovanou budoucí hodnotu (BH). Mohu pak pro příklad roční (n = 1) půjčky kamarádovi, chtít vypočítat, jaká by byla suma peněz, které mu půjčím, abych na této transakci vydělal 1,100.000,- Kč (BH = 1,100.000,- Kč) při představě, že chci zhodnotit tyto půjčené peníze úrokovou sazbou 10% p.a. (úrok = 0.10)

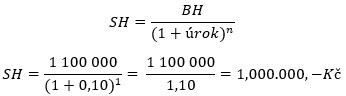
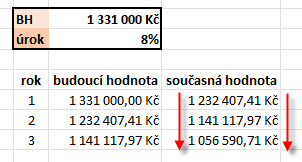
   Pro zhodnocení mé jednoroční investice na konečnou částku 1,100.000,- Kč budu při požadovaném úroku 10% p.a. muset realizovat půjčku ve výši 1,000.000,- Kč. Stejně tak mohu použít tento vzorec pro příklad s pořízením tříletého termínovaného vkladu (n = 3) z minulého článku, kdy jsem vyměnil jednomilionovou půjčku právě za investici do takového investičního produktu s 10% sazbou p.a. (úrok = 0,10) a s vypočítanou výši konečné částky tříletého vkladu ve výši 1,331.000,- Kč. Pokud bych nasadil tento vzorec také na tento příklad, tedy požadoval zjistit kolik, mám na termínovaný vklad vložit, abych měl na konci tříletého období k dispozici 1,331.000,- Kč při nabízeném úroku 10% p.a., vypadal by výpočet následovně:   

   Výsledek je očekávaný 1,000.000,- Kč, jako potřebná částka k investici s požadovaným tříletým zhodnocením. Mohu pak tento vzorec „rozpitvat“ na jednotlivé postupné kroky v excelovské tabulce, kde jsou diskontovány jednotlivé roky trvání investice od budoucí hodnoty k současné.

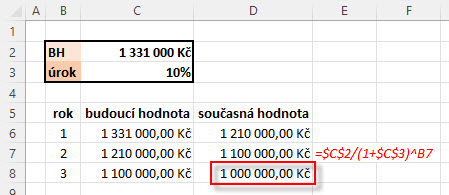
   Přestože to vypadá jednoduše a pochopitelně, hledání odpovědi na otázku velikosti současné hodnoty při očekávané konkrétní budoucí hodnotě poodkrývá tři základní závislosti světa investičních nástrojů s pevným příjmem (fixed-income) navázaných na úrokovou sazbu. Investiční produkt s pevným příjmem totiž nabízí jakousi spočítatelnou budoucí hodnotu a nabízí se k pořízení za zcela konkrétní cenu, kterou mohu vidět ve své obchodní platformě. Mohu si nyní zjednodušeně představit, že tříletý termínovaný vklad není bankovním spořícím produktem, ale je jakýmsi tříletým investičním nástrojem, pro který jsem si spočítal budoucí hodnotu 1,331.000,- Kč při aktuální úrokové sazbě 10% p.a., která generuje právě tuto budoucí hodnotu. Mohu pak nad existencí a pořízením tohoto investičního produktu provést tato zamyšlení:

1/ Aktuální cena investičního nástroje na trhu 

   Aktuálním pohledem do své obchodní platformy mohu zjistit, že tento investiční nástroj se nenabízí za 1,000.000,- Kč, ale jeho cena na trhu je 900.000,- Kč. Protože vím, že všechny platby v budoucnosti vyplývající z držení investičního nástroje budou v součtu 1,331.000,- Kč, bude mé zhodnocení investice vyšší než 10% p.a. Stejně tak naopak, pokud by tento investiční produkt s pevným příjmem byl na trhu k mání za aktuální cenu ve výši 1,150.000,- Kč, budu mít celkové zhodnocení zamýšlené investice nižší než 10% p.a.

2/ Aktuální úroková sazba na trhu

  Modelový investiční nástroj se nabízí za férovou cenu 1,000.000,- Kč a při aktuální úrokové sazbě 10% p.a. je jeho budoucí hodnota 1,331.000,- Kč. Ihned po jeho pořízení se ale úroková sazba zvýší o +2% a bude +12% p.a.. Jaký to bude mít vliv na cenu tohoto investičního nástroje?

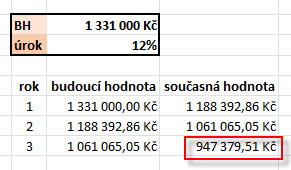
   Svého cíle 1,331.000,- Kč budoucí hodnoty investice po třech letech dosáhnu při zvýšených úrokových sazbách za nižší současnou hodnotu. Podle tabulky s diskontováním budoucí hodnoty z obrázku výše mohu zjistit, že by cena takového nástroje měla klesnout na 947.379,51 Kč. Pokud by naopak úroková sazba ihned po pořízení investičního nástroje klesla o -2% na úroveň +8% p.a., mohu provedeným diskontováním pozorovat tento výsledek.

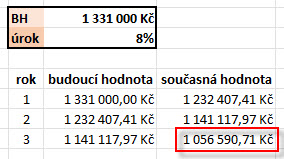
   Cena investičního nástroje by měla vzrůst, protož k naplnění budoucího investičního cíle 1,331.000,- Kč při snížené úrokové sazbě bude zapotřebí větší prvotní investice.       

3/ Klesání současné hodnoty investice směrem do budoucnosti

   Pro danou úrokovou sazbu vyznačenou pro daný investiční nástroj s pevným výnosem platí, že současná hodnota investice směrem do budoucnosti (ke splatnosti) klesá. S postupem času mohu přijímat stále vyšší část budoucí hodnoty investičního nástroje, který mohu dále reinvestovat a akumulovat další příjem, tím mám možnost dosáhnout investičního tříletého cíle s méně než zbylými investovanými prostředky.

   Vypočítat současnou hodnotu lze pomocí jednoduchého vzorce uvedeného výše pro zadané podmínky a pro stanovenou očekávanou budoucí hodnotu u investičních produktů, které nabízejí zhodnocení nějakou úrokovou sazbou, která je aplikována za nějaký časový úsek, například jedenkrát za rok (p.a.) a s touto frekvencí jsou také tyto peněžní toky připisovány a opětovně úročeny podle sjednaných podmínek. Protože jsou předmětem mého zájmu dluhopisy, nebude tento jednoduchý výpočet současné hodnoty pro tento účel patrně zcela takto jednoduše stačit. Držení dluhopisu poskytuje slíbené úročení mé investice ve formě výplaty pravidelného kupónu se sazbou z nominálu dluhopisu vyznačenou v jeho prospektu, nicméně jeho držení postrádá výhodu připisování úroků a jeho opětovného úročení. Přijatý úrok z kupónu je totiž držiteli dluhopisu vyplacen a o jeho dalším osudu rozhoduje jeho příjemce.  

   K představě, jak bude možné se dobrat k parametrům dluhopisu a provádět jejich nejjednodušší vyhodnocování je zapotřebí porozumět řešení již popsaných úloh a tyto potom aplikovat na to, co mě může v obchodní praxi potkat. Držení dluhopisu s pevným kupónem vyjádřeným úrokovou sazbou představuje vynaložení nějaké částky na jeho pořízení a poté do doby splatnosti inkasuji slibovaný kupón, společně s posledním kupónem je mi vrácena částka představující nominál dluhopisu. Nemusím nyní nakonec uvažovat jenom o dluhopisu, ale například o jakékoliv jinak nazvané investici s pevným příjmem v budoucnosti. Nabízí se mi například pořízení investičního nástroje, který po dobu pěti let přináší periodický každoroční příjem ve výši +500 USD a na konci pátého roku obdržím (kromě poslední pětistovky dolarů) částku 20.000,- USD. Toto zadání je patrné na obrázku níže.

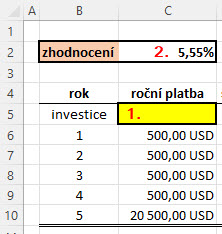
   Nyní mě bude zajímat, jakou cenu (1) bych měl za tento investiční nástroj nyní zaplatit, aby pro mě tato investice představovala zhodnocení 5.55% p.a. (2), takovou úrokovou sazbu bych považoval za vhodnou pro svůj investiční plán, můžu nakonec vycházet z okolní reality, když ve chvíli, kdy píšu tyto řádky se aktuální úrokové sazby v USA pohybují kolem 4% p.a. K tomuto číslu – pořizovací hodnotě tohoto investičního nástroje, se doberu za použití výše uvedeného vzorce k diskontování budoucí hodnoty na současnou cenu, a to tak, že budu zjišťovat, jaká je aktuální současná hodnota každé v budoucnosti přijaté platby a potom tyto jednotlivé položky sečtu. Budu diskontovat mnou požadovanou úrokovou mírou (5.55%) každý budoucí peněžní tok, který se dostane k mým rukám a bude mě tak zajímat, jaká je hodnota každé této jednotlivé platby a samozřejmě hodnota jejich součtu. Vzorec pro takový celkový součet je níže.   

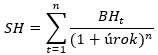
    Bude to znamenat, že vezmu 4x každou pětistovku dolarů, kterou v budoucnosti obdržím společně s pátou pětistovkou obohacenou o splátku nominálu investičního nástroje a provedu jejich diskontování podle vzorce z úvodu článku a podle období, kdy tuto platbu v budoucnosti obdržím. Mohu proto sumu ze vzorce výše rozepsat podle mého příkladu na zcela konkrétní výpočetní postup:

   Nebudu se významně namáhat s kalkulačkou a svěřím tento úkon excelovské tabulce, abych zjistil hodnotu z tohoto mírně dlouhého vzorce.

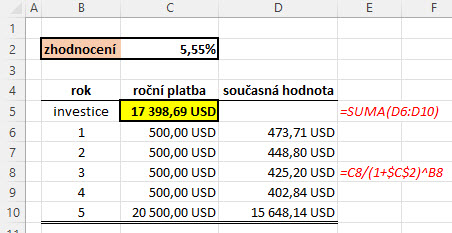
   Mohu vypozorovat, že výsledek diskontování na aktuální cenu takto strukturované investice by přinesl hodnotu současné ceny ve výši 17.398,69 USD. V jednotlivých řádcích obrázku jsou patrné diskontované ceny (sloupec „současná hodnota“) pro každé budoucí cash flow do mých rukou, ve žlutě podbarvené buňce je pak výsledek jako prostý součet těchto jednotlivých diskontovaných položek (červeně v obrázku příklad excelovského vzorce pro výpočet diskontované hodnoty 500,- USD pro třetí rok držení investičního nástroje). Ve skutečnosti budu, s ohledem na téma této série článků, tento vzorec a postup aplikovat také na ocenění dluhopisů, pouze předesílám, že tento výpočet bude založen na principu zjištění současné ceny všech obdržených kupónů diskontováním jejich postupných příjmů najednou a diskontováním nominální hodnoty dluhopisu, výsledná cena dluhopisu pak bude součtem těchto hodnot, nebudu tak tvořit tabulku o mnoha řádcích představujících každou periodu s příjmem peněžního toku, ale využiji jeden vzorec pro diskontování všech těchto peněžních toků a jeden vzorec na diskontování nominálu.   

   Otázka hledání současné hodnoty budoucí investice může být také postavena poněkud jinak. Mohu pozorovat (například v obchodní platformě) investiční nástroj s pevně stanoveným příjmem, který se nabízí k mé zamýšlené investici s tím, že vidím jeho současnou hodnotu SH a znám všechny budoucí příjmy BH_t , jak budou postupně „připlouvat“ na můj obchodní účet,  neznám ale úrokovou sazbu úrok, kterou tato investice představuje, abych mohl jednoduše vyhodnotit, s jakým zhodnocením mé investice vlastně mohu počítat. Na rozdíl od předchozího případu, kdy znám všechny budoucí peněžní toky a úrokovou sazbu pro hledání současné ceny investice nyní, při známé současné ceně investice a všech budoucích peněžních toků, budu hledat úrokovou sazbu, která tuto investici bude charakterizovat. Mohu pak toto zobrazit níže na obrázku.      

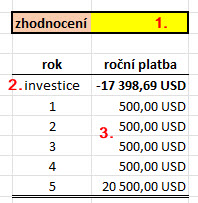
   Otázka tak nyní zní, jakou dostanu výslednou úrokovou sazbu p.a. (1) při známé pořizovací hodnotě investice -17.398,69 USD (2) a všech poznaných budoucích peněžních tocích (3)?

   Vypočítat počáteční hodnotu investice při známé úrokové sazbě podle vzorce pro diskontování peněžních toků je jednoduché, dosadíme hodnoty do vzorců a je hotovo, toto můžeme udělat v nejhorším případě i ručně (viz rozepsaný vzorec sumy postupných výpočtů v odstavci výše). Provést ale výpočet úrokové sazby zhodnocující mou investici o známé současné hodnotě investice a poznaných budoucích peněžních tocích tak jednoduché není. Pokud bych chtěl ze vzorce výše toto provádět, musel bych volit metodu postupné aproximace, tedy spočítat při nějaké zvolené úrokové sazbě výslednou současnou hodnotu a poté zvolit jinou úrokovou sazbu a spočítat další výslednou současnou hodnotu. Pokud bych použitím takto zvolených „náhodných“ úrokových sazeb obdržel výsledky současné hodnoty, které jsou menší než je aktuální skutečná hodnota investičního nástroje a výsledky, které jsou větší než je aktuální skutečná hodnota investičního nástroje, mohl bych je aproximovat do takové úrokové sazby, která by přesně odpovídala současné skutečné hodnotě investičního nástroje, kterou bych mohl pozorovat například ve své obchodní platformě. Toto je však značně náročný počtářský úkon, který hravě zvládne Excel použitím funkce =MÍRA.VÝNOSNOSTI. Vyhledat hodnotu Vnitřního Výnosového Procenta (Internal Rate of Return IRR), tak se tato aproximovaná hodnota úrokové sazby také nazývá, je pak pomocí této excelovské formule velmi jednoduché. Vzorec pro výpočet Vnitřního Výnosového Procenta nasazený do excelovské tabulky pracuje technikou iterace, kde postupně zpřesňuje nastíněný ruční výpočet na jednu stotisícinu procenta, na výsledek se tak lze spolehnout.    

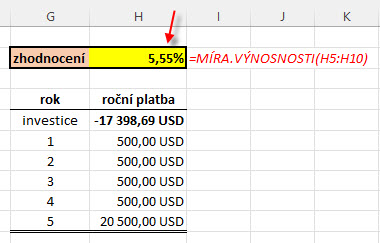
   Nasazení vzorce pro výpočet Vnitřního Výnosového Procenta – hledané úrokové sazby zhodnocení mé investice o dané počáteční hodnotě a poznaných budoucích peněžních tocích, mi vypočítá hodnotu +5.55% p.a., tedy potvrzuje, že nalezená hodnota je správná. Pokud jsem při této zadané úrokové sazbě a stejných budoucích peněžních tocích zjistil nejdříve podle vzorce o hledání současné hodnoty investice její počáteční hodnotu, potom jsem pomocí této počáteční hodnotě a poznaných budoucích peněžních tocích pomocí výpočtu vnitřního výnosového procenta zjistil požadovanou úrokovou sazbu reprezentující celkové zhodnocení mé investice.

   Mohu také vyzkoušet, jak by se změnilo celkové zhodnocení investice, pokud bych při zadaných podmínek, které generují budoucí peněžní toky, pořídil investici za jinou cenu, než za -17.398,69 USD, když tato pořizovací cena představuje zhodnocení +5.55% p.a.

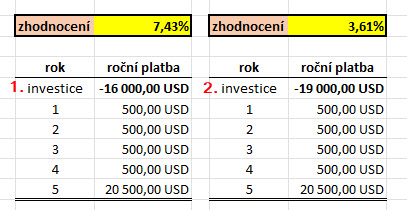
   Pořízení investičního nástroje za nižší cenu 16.000,- USD (1) by znamenalo vyšší zhodnocení na úrovni +7.43% p.a., pořízení investičního nástroje za vyšší cenu 19.000,- USD (2) by znamenalo nižší zhodnocení na úrovni -3.61% p.a.. Můžu tak opět potvrdit pravidlo 2/ výše v článku o souvislosti výše úrokové sazby a pořizovací ceny investice. 

   Zásadním poznáním v pochopení fungování dluhopisů je poznat principy tvorby jeho aktuální ceny. Principy jsou obecné pro investici do čehokoliv, co přináší jakýsi pevný příjem v budoucnosti (nebo mám alespoň představu o tomto budoucím příjmu). Mohu tak tyto výpočty aplikovat na cokoliv diskontováním těchto budoucích příjmů do jejich současné hodnoty a jejich součtem pak ocenit současnou hodnotu této investice nebo z těchto diskontovaných cen rozpoznat výnosnost zamýšlené investice. Všechny poznatky pak budou aplikovány na dluhopisy, které ve svých různých formách a podobách představují právě takovou investici, většinou nabízejí výplaty kupónů vyjádřené procentem z jejich nominální hodnoty s nějakou budoucí frekvencí (od příštího článku již budu používat jiný termín než „nominál“) a slibují u jejich splatnosti vrácení hodnoty tohoto nominálu. Příště to tak již bude opravdu jen o dluhopisech….:c)

   Komentáře a příspěvky k tomuto článku prosím směrujte do Diskuzního fóra do tohoto vlákna :c)