
Obchodovat opce lze tak, že na příslušný požadovaný opční kontrakt jednoduše kliknu do své obchodní platformy a zadám příkaz k jeho nákupu. To dnes chápe každý. Kde se ale berou všechna ta čísla s cenami jednotlivých kontraktů na jednotlivých strikes a v jednotlivých expiracích a jak jsou vlastně stanovována? Generují je burzovní servery, které pracují s různými algoritmy a modely, které na základě dostupných údajů vypočítávají jednotlivé ceny opčních kontraktů, které jsou pak viditelné v obchodních platformách. Pominu nyní vliv nabídky a poptávky na cenu opčního kontraktu a pokusím se jednoduše ukázat, bez nějakého „vědeckého podtextu“, jak jsou takové ceny stanoveny.
Základem výpočtu ceny opčního kontraktu je nějaký matematický model. Modelů pro výpočet takové ceny je spousta a jejich struktura je velmi odlišná. Nebudu se zabývat popisováním a odlišnostmi jednotlivých modelů, pokusím se objasnit výpočetní schéma nejznámějšího ze všech modelů, a to Black – Scholesova modelu. Při prvním pohledu na obrázek s matematickým tvarem tohoto modelu to vypadá jako nepochopitelná změť znaků, výrazů a matematických symbolů. Tento chuchvalec pak stojí alespoň za mírné rozpletení, aby došlo k nějakému alespoň mírnému pochopení a následnému praktickému využití. Na internetu existuje množství sofistikovaných aplikací, které Vám po zadání vstupních údajů vypočítají teoretickou hodnotu opcí, ale je to pořád v těch aplikacích nějak zamontováno, jak se k těmto cenám opcí výpočtem došlo. Pokud bych chtěl takovým aplikacím věřit, musím zjistit, jestli „mluví pravdu“. To nezjistím jinak než pochopením základní kostry výpočtu ceny opcí, které tyto aplikace provádějí.
Z Black-Scholesova vzorce pro výpočet teoretické hodnoty opcí vyplývá, že ke stanovení ceny opce potřebujeme mít určité vstupní veličiny, bez jejichž znalosti takovou cenu nemůžeme spočítat, těmito hodnotami jsou:
1/ Cena podkladového aktiva – cena za kterou se momentálně obchoduje
2/ Strike – na kterém strike chceme cenu vypočítat
3/ Čas trvání opčního kontraktu – doba života opce
4/ Volatilita
5/ Dividendy – pokud se za života sledované opce vyplácejí
6/ Úroková míra – existující za života opce
Z obrázku vyjadřující Black-Scholesův vzorec vyplývá, že vlastně celá podstata výpočtu teoretické ceny opce je jen o jednoduchém pochopení jednotlivých významů vzorce.
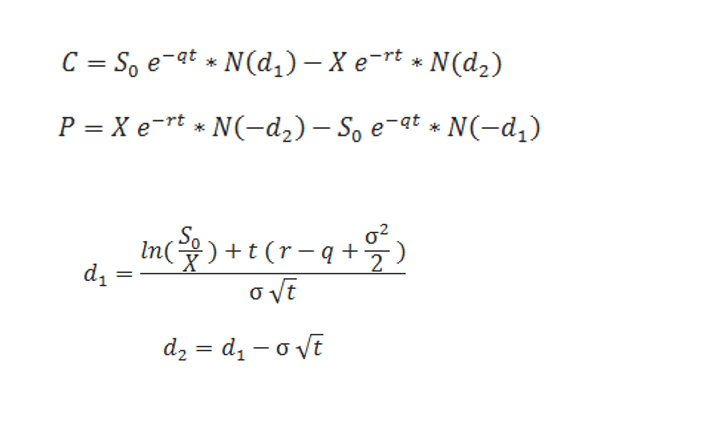
První dva řádky – vzorce – pak vyjadřují jednotlivé postupy pro výpočet ceny Call opce a Put opce, na dalších dvou řádcích je výpočet jakési hodnoty d1 a d2, které jsou použity ve vzorci v prvních dvou řádcích. Nebudu uvádět, co jednotlivé výrazy znamenají, protože vzorce se v různých pramenech v tomto označování výrazů liší, ale zkusím si vzorec převést na výše uvedené veličiny „v češtině“. Pokud tedy dosadím za jednotlivé symboly česká slova, tak je možné vzorce lépe „rozklíčovat“ a také možná pochopit.

Na první pohled je zřejmé, že se jedná vlastně o složeninu tvořenou vždy z rozdílu dvou velmi podobných hodnot. K lepšímu grafickému pochopení tohoto rozdílu hodnot v „počeštělém vzorci“ označím tyto jednotlivé části složitého vzorce.
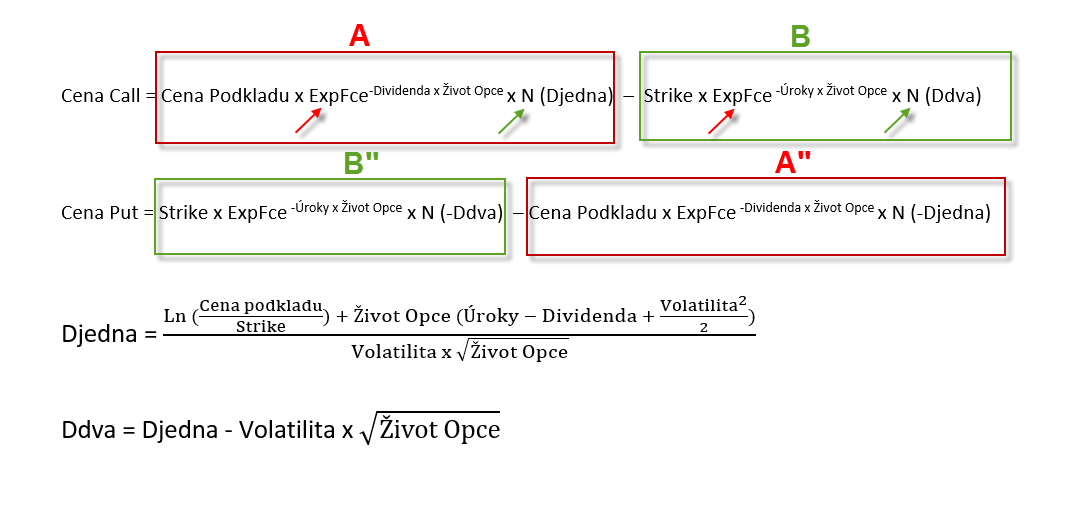
Pokud si tyto složeniny takto převedu do češtiny, tak je zjevné, že cena opce Call je tvořena Cenou podkladu upravenou o „nějakou hodnotu“ (část A) od které je odečítána hodnota Strike opce upravená o „nějakou hodnotu“ (část B). U výpočtu ceny opce Put je situace obrácená, kdy se odečítá od hodnoty Strike upravenou o „nějakou hodnotu“ (část B“) hodnota Ceny podkladu upravenou o „nějakou hodnotu“ (část A“).
Tento výpočet pak respektuje základní logiku, kdy cena opčního kontraktu se odvíjí od jeho vnitřní hodnoty – hodnoty, kterou je opce „v penězích“. Pokud tedy cena Call opce je v úplném zjednodušení vypočtena jako Cena podkladu mínus Strike a k tomu je přidáno „ještě něco dalšího“, tak při ceně akcie 145 USD bude mít Call opce se strike 135 (tedy 10 bodu „v penězích“) cenu 145 USD (cena akcie) -135 USD (strike) = 10 USD a „ještě něco dalšího“, cena takové opce na tomto strike 135 tak bude minimálně těchto 10 USD. Hodnotu „ještě něco dalšího“ bych pak mohl jednoduše pojmenovat jako opční prémium. Pokud by naopak byla hodnota strike „mimo peníze“, tedy nad současnou obchodovanou cenou, například bych chtěl vypočítat hodnotu Call opce se strike 150, potom by tímto rozdílem byla hodnota „žádná vnitřní hodnota“, konkrétně cena 145 USD (cena akcie) -150 USD (strike) = -5 USD a „ještě něco dalšího“. Protože vnitřní hodnota opce nemůže být záporná ale nejméně nula, byla by výsledkem tohoto výpočtu právě hodnota označovaná jako „ještě něco dalšího“ – tedy čisté prémium. Ve úplném a nejjednodušším shrnutí by tedy taková matematická interpretace BS modelu mohla znít, že opce „ITM – v penězích“ má cenu „vnitřní hodnoty + prémium“ a opce „OTM – mimo peníze“ má pak hodnotu „pouze prémium“.
Smyslem tohoto vzorce z takové „české ptačí perspektivy“ je, že opce Call i Put na stejném strike by měly mít sobě navzájem odpovídající hodnoty podle tohoto strike v závislosti na ceně podkladu. Pokud se podívám na vzorec z pohledu hodnot, které známe a které si můžeme do vzorce jednoduše dosadit (Cena Podkladu, Strike, Život opce, Volatilita, Úroky a Dividenda), potom nám zbývají pouze dva výrazy, které je potřeba rozklíčovat, a které jsou v obdélníku A a B označeny šipkami:
e – neboli Exponenciální funkce (červené šipky), jejímž exponentem je v jednom případě součin -Dividenda a Život Opce (ve vzorci A) a v druhém (ve vzorci B) je exponentem součin -Úroky a Život Opce. Z této exponenciální funkce nám bude stačit za zaznamenání, že pokud nebude za Života Opce vyplácena Dividenda, potom bude hodnota Dividenda = 0, celý exponent bude nula a cokoliv na „nultou“ je vždycky jedna, takže hodnota této exponenciální funkce bude také jedna a nebude mít na počítanou cenu opce žádný vliv. To samé platí u druhé exponenciální funkce, kdy na vliv ceny opce mají vliv Úroky nebo doba Života Opce, pokud bude hodnota Úroků nula nebo hodnota Života opce nula (opce je úplně těsně před expirací), tak obdobně bude koeficient nula a celá druhá exponenciální funkce bude (opět cokoliv na „nultou“ je jedna) mít hodnotu jedna a nebude mít pak na cenu počítané opce žádný vliv. Hodnotu exponenciální funkce nám hravě vypočítá Excel (funkce EXP), takže si nemusíme s tímto výpočtem lámat hlavu.
N – neboli Distribuční funkce Normálního rozdělení (zelené šipky), která má ve vzorci pro výpočet opcí argumenty Djedna a Ddva. Jejich výpočet převedený do češtiny je vidět na screenu výše. Tyto argumenty jsou jednoduše spočítatelné v Excelu, protože obsahují pouze námi známé hodnoty (Cena Podkladu, Strike, Život opce, Volatilita, Úroky a Dividenda), zbytek výpočtu tvoří jednoduché matematické operace. Také hodnotu distribuční funkce nám spočítá Excel (funkce NORMSDIST), takže nemusíme mít obavu, že toto bude pro nematematika nějaký nepřekonatelný problém.
Celý výpočet teoretické hodnoty opce Call nebo Put bychom potom podle tohoto modelu mohli zjednodušit tak, že nejdříve vypočítáme hodnoty Djedna a Ddva, jako argumenty distribuční funkce, která se nám v Black-Scholesově modelu objevuje a tyto potom dosadit do samotného vzorce pro výpočet jednotlivých cen pro Call i Put.
No a k čemu je to celé vlastně dobré a jak znalosti a pochopení tohoto vzorce využít pro vlastní obchodování?
Vše by mohlo prakticky vyplynout z převedení celého vzorce do Excelu, který by se mohl stát základem pro jednoduché opční výpočty. Protože by bylo dosti kostrbaté a nepraktické jednotlivé části výpočtu opční ceny zadávat do Excelu pomocí logických funkcí, udělal jsem to tak, že jsem v Excelu vytvořil pro jednotlivé ceny opcí Call a Put samostatné funkce. Přesně podle postupu s předešlého výpočtu jsem nejdříve „Excelu řekl“, jak má vypočítat hodnoty Djedna a Ddva, jako argumenty distribuční funkce, abych potom tyto vypočítané argumenty vložil do funkce, která přímo vypočte cenu Call nebo Put na zadaném strike podle příslušných parametrů. V Excelu, který je přiložen k tomuto příspěvku jsou vytvořeny speciální funkce CallCena a PutCena, také můžete tyto funkce vidět, jak jsou ve VBA naprogramovány a tyto si můžete například zkopírovat do Vašeho excelu a potom s těmito funkcemi běžně pracovat (jednoduše si zkopírujete celý viditelný text kódu). Pro ty, kteří neví, jak se k funkcím ve VBA dostat – kliknete na kartu „Vývojář“, potom na „Visual Basic“ a uvedený script můžete ze sekce Module celý kopírovat a přenášet do Vašeho Excelu, kde si vašeho „Vývojáře“ a okno „Visual Basic“ stejným způsobem otevřete. Zdatnější znalci excelu uvidí, že fukce jsou ve VBA vytvořeny „otrockým“ přepisem uvedených vzorců Black-Scholesova modelu do VBA, téměř nic světoborného. (při otevírání excelovského sešitu musíte na výzvu programu „povolit makra“)
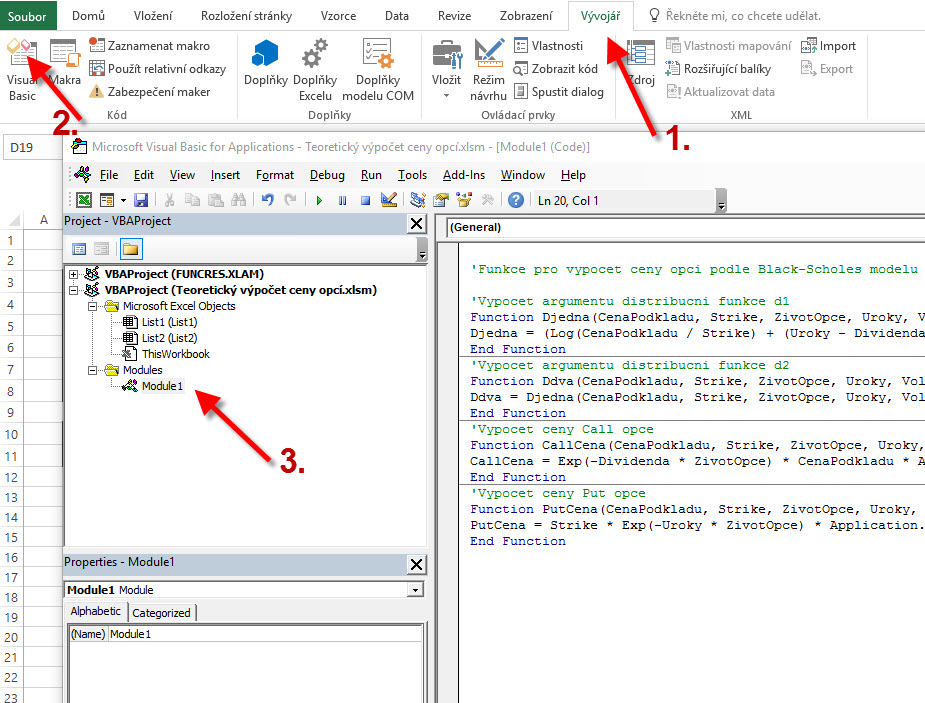
Pokud si takový svůj Excel se zkopírovaným kódem otevřete nebo využijete přiložený, tak můžete přímo v buňce zadávat výpočet ceny Call a Put opcí, tyto funkce CallCena a PutCena mají vždy šest argumentů, které musíte do funkce dosadit, těmito argumenty jsou CenaPodkladu, Strike, ZivotOpce, Uroky, Volatilita, Dividenda, tedy ty známé argumenty, které cenu opce tvoří. Po správném zadání všech argumentů se nám v buňce s funkcí objeví cena příslušné opce. V přiloženém Excelu jsou jednotlivé argumenty uvedeny v levé části v bledě modře označených buňkách tabulky.
Aby byly jednotlivé argumenty funkce CallCena a PutCena zadány správně pro Vaše další výpočty, tak musíte vědět, že:
1/ Cena podkladového aktiva – zadává se jako klasické číslo
2/ Strike – na kterém strike chceme cenu vypočítat – zadává se jako klasické číslo
3/ Život opce – zadává se jako klasické číslo, které je rozdílem data pořízení opce a data zbavení se opce, vše přepočteno na roční bázi, takže tento výsledný rozdíl dělíme číslem 365
4/ Volatilita – zadává se v %
5/ Dividendy – zadává se v % výplatním poměru k ceně podkladového aktiva a v její anualizovaném tvaru – např. XYZ vyplácí 4 x ročně 0,50 USD dividendu, tedy celkem 2 USD/rok. Cena XYZ je 50 USD, výsledkem je 2/50 = 0,04 = 4%
6/ Úroková míra za života opce – jaká je aktuální úroková míra US státních dluhopisů v období do expirace opčního kontraktu
Pokud takto dosadíte tyto hodnoty do fukce CallCena a PutCena, objeví se Vám ve výsledku ceny opcí. Podívejte se do ukázkového Excelu, jak jsou tam tyto hodnoty zadány a uvidíte, že práce s takovou tabulkou je velmi jednoduchá. Po zadání hodnot do modrých buněk nejenže uvidíte cenu Call a Put opce na zadaném strike, ale také se vám vygeneruje jednoduchý opční řetězec s pěti strikes na každou stranu od ATM hodnoty, sestavený právě z těchto naprogramovaných funkcí (v tabulce je také vidět buňku „Krok Strike“ pro vyplnění například hodnotou 2.5, kdyby strikes v opčním řetězci byly od sebe takto vzdálené).
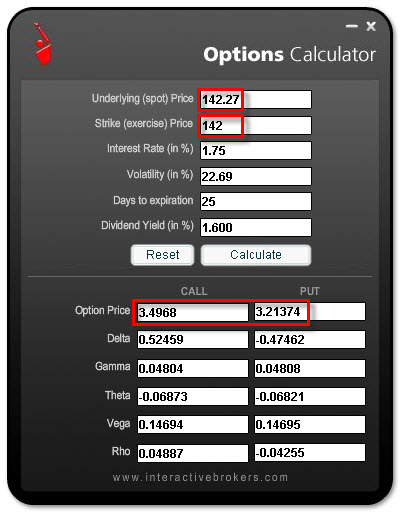
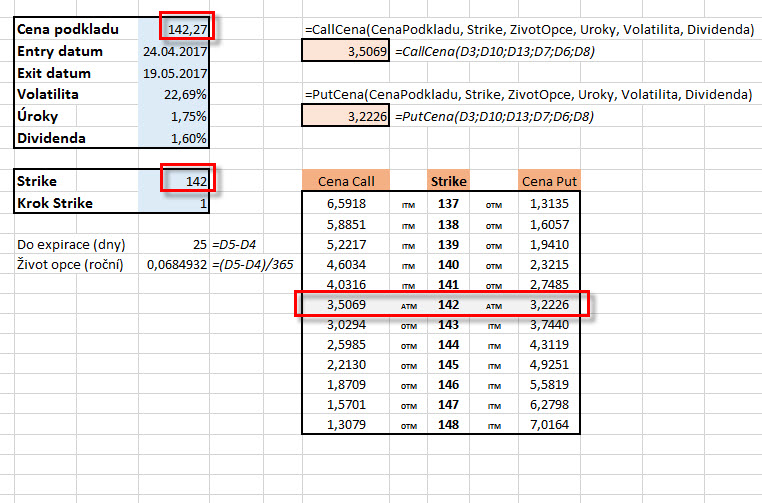 Abychom si mohli potvrdit a ověřit, že funkce v Excelu pracují správně, připojuji screen se zadanou cenou a parametry ve srovnání s aplikací, kterou si můžete stáhnout například ze stránek Interactive Brokers. Do tabulky jsou zadány současné ceny akcie AAPL obchodující se za 142,27 USD, která například za dobu života opce vyplácí čtvrtletní dividendu ve výši 0,57 USD/akcii (potom do řádku Dividenda uvedeme údaj podle výpočtu: 0,57 x 4 = 2,28 USD/rok, cena akcie je 142,47 USD, potom 2,28 USD/142,47 USD = 1.60%). Doba života opce je 25 dnů tak, aby zahrnovala také tuto vyplácenou dividendu. Hodnota Implied Volatility byla vyplněna hodnotou 22,69% a úroky byly stanoveny ve výši 1,75% p.a. Ceny jsou téměř identické, jak ve vytvořeném Excelu tak v aplikaci z IB, rozdíly jsou způsobeny pravděpodobně zaokrouhlováním. Porovnával jsem ceny Call i Put opcí se strike 142.
Abychom si mohli potvrdit a ověřit, že funkce v Excelu pracují správně, připojuji screen se zadanou cenou a parametry ve srovnání s aplikací, kterou si můžete stáhnout například ze stránek Interactive Brokers. Do tabulky jsou zadány současné ceny akcie AAPL obchodující se za 142,27 USD, která například za dobu života opce vyplácí čtvrtletní dividendu ve výši 0,57 USD/akcii (potom do řádku Dividenda uvedeme údaj podle výpočtu: 0,57 x 4 = 2,28 USD/rok, cena akcie je 142,47 USD, potom 2,28 USD/142,47 USD = 1.60%). Doba života opce je 25 dnů tak, aby zahrnovala také tuto vyplácenou dividendu. Hodnota Implied Volatility byla vyplněna hodnotou 22,69% a úroky byly stanoveny ve výši 1,75% p.a. Ceny jsou téměř identické, jak ve vytvořeném Excelu tak v aplikaci z IB, rozdíly jsou způsobeny pravděpodobně zaokrouhlováním. Porovnával jsem ceny Call i Put opcí se strike 142.
Přestože jsem uvedl, že se nebudu zabývat jinými modely než Black-Scholesovým modelem, uvedu srovnání výpočtu ceny opcí podle jiného známého opčního oceňovacího modelu – Binomického modelu, jehož kalkulaci můžete využít v aplikaci na stránkách Livevol. Pokud zadám stejné parametry a provedu takový výpočet ceny opcí na strike 142, uvidím výpočet ceny, který se liší od BS modelu o cca +/- 0,20 USD u každé s opcí. Protože nevím, jak byla aplikace binomického modelu tvořena (ani se o ni nebudu pokoušet) tak je zde významný rozdíl. Jak bych si ji měl vysvětlit nebo kterému modelu více věřit?
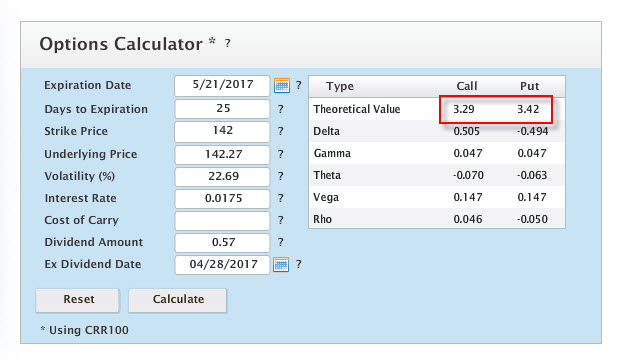
Nebudu se pouštět do kritiky jednotlivých modelů a složitě matematicky dokazovat, kde například udělali autoři BS modelu chybu, protože takových fundovaných diskuzí je k dispozici velké množství a přebrodit se přes ně představuje být vybaven matematickými dovednostmi nacházejícími se za alespoň mým horizontem poznání. V jedné funkcionalitě ale BS model není úplně přesný, pokud je matematicky vyjádřen jako na výše uvedených obrázcích a dosti silně se rozchází s obchodní realitou. Pokud do jeho výpočtu zahrnu výplatu dividendy způsobem, jakým jsem ji popsal, tedy v jejím anualizovaném tvaru, tak to znamená, že cena opce osahuje takovou vyplácenou dividendu, a to tak, jako kdyby každý den vyplácela dividendu ve výši vypočtenou na tento jeden den. Takto to ale ve skutečnosti není, protože výše dividendy, pokud se vyplácí za dobu života opce, se zcela promítá do hodnoty Put opce, aby bezprostředně po její výplatě na Ex-Dividend Day se v hodnotě této Put opce téměř neodrážela. Tuto skutečnost ve svém výpočtu tak lépe momentálně zachycuje výpočet podle binomického modelu podle obrázku výše. Nevím ale, jestli je to „dokonalostí“ binomického modelu nebo nějaká jiná příčina.
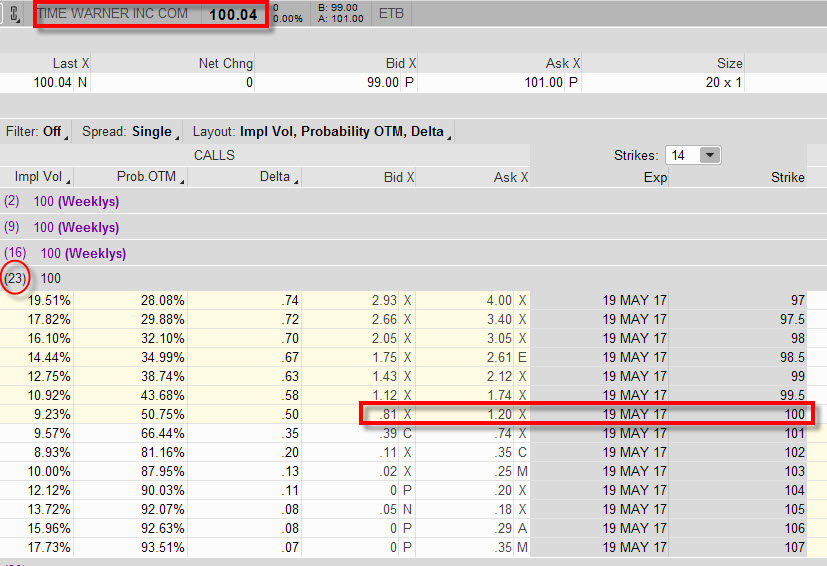
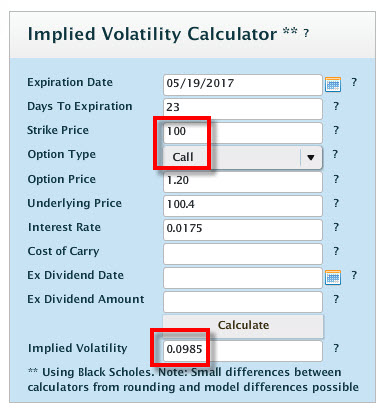
Pokud jsou k výpočtu ceny opce podle takového BS modelu nutné mít k dispozici údaje o Ceně Podkladu, Strike, Délce života opce, Implied Volatilitě, Úroku a Dividendě, pak můžeme, pokud známe právě počítanou cenu opce například z opční obchodní platformy, vypočítat každou jednotlivou dílčí hodnotu tvořící takový výpočet. Z praktického hlediska je totiž na první pohled jasné, že na cenu opce má největší vliv hodnota Implied Volatility, která je pak v takovém výpočtu „největším hráčem“. Pokud bychom totiž například zjišťovali cenu opcí na stejný strike u akcií, které se obchodují za stejnou cenu, mají stejnou dobu do expirace za stejných úrokových podmínek a například nevyplácejí dividendu, pak by měly tyto opce mít stejnou hodnotu – pokud by ovšem měly stejnou hodnotu Implied Volatility. Z této jednoduché úvahy pak vyplývá, že Implied Volatilita je tím největším hybatelem ceny opčních kontraktů, její výše se do ceny okamžitě a velmi razantně promítá a tvoří její cenu. Pokud bych chtěl tuto skutečnost demonstrovat na nějaké obchodní realitě, tak na níže uvedeném obrázku je vidět momentální cena Call opcí na strike 100 akciového titulu Time Warner Inc (TWX), které se obchoduje cca za 100 USD a má Implied Volatilitu na hodnotě cca 10%, opce má 23 dnů do expirace. Cena opcí na strike 100 se pohybuje mezi 0,81 – 1,20 USD.
Na dalším obrázku je vidět opční řetězec akciového titulu Masimo Corp. (MASI), který se obchoduje za téměř totožnou cenu 100 USD, ovšem hodnota Implied Volatility je zhruba 30%, tedy hodnota třikrát vyšší než u předcházejícího titulu, opce má opět 23 dnů do expirace. Cena opcí na strike 100 se pak pohybuje mezi 3,50 – 4,50 USD.
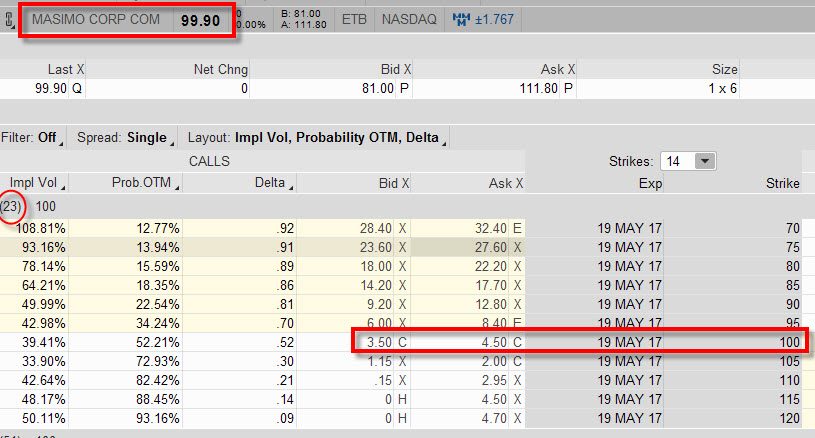
Cena opcí na stejném strike se stejnou expirací za stejných úrokových podmínek a bez dividendy se pak diametrálně odlišuje. Hodnoty opcí u titulu s vyšší Implied Volatilitou jsou více než třikrát vyšší. Vše je způsobeno právě touto Implied Volatilitou, všechny ostatní podmínky pro výpočet ceny opcí jsou totiž identické.
Protože známe ceny jednotlivých opcí a známe všechny ostatní parametry, dá se pak pomocí matematického oceňovacího modelu vypočítat, jaká je právě hodnota této Implied Volatility. Tyto hodnoty mohou být velmi užitečné k obchodnímu použití, protože obchodování opcí je především o obchodování volatility. Vzorec a technika výpočtu Implied Volatility podle BS modelu je dosti sofistikovaná, naštěstí jsou však volně k dispozici aplikace, které nám podle zadaných podmínek takovou hodnotu Implied Volatility vypočítají. Například na Livevol můžeme jednu takovou najít. Na obrázku je vidět výpočet takové Impied Volatility právě u titulu Time Warner pro strike 100 za ceny opce ve výši 1,20 USD. Po zadání expirace a úroků vidíme výpočet momentální Implied Volatility této opce ve výši 9,85%, což odpovídá údajům z předcházejících obrázků.
Obchodování opcí vypadá mnohdy velmi komplikované a jakoby teoreticky náročné. Myslím si, že není třeba se takových vlastností vůbec obávat a není zase tak obtížné jim alespoň jednoduše porozumět. Excel s teoretickým výpočtem opčních cen, o kterém psal v tomto článku, si můžete stáhnou zde Teoretický výpočet ceny opcí a vyzkoušet si některé popisované funkcionality nebo se podívat na jednoduchý VBA kód výpočtů a funkcí.
Sleduj facebook, napiš e-mail nebo tweet
Prosím tě, ve vzorečcích je všude uvedeno „ln“, tedy přirozený logaritmus, ale v té VBA funkci se volá excelovská funkce Log(), což by (podle http://www.excelfunctions.net/Excel-Log-Function.html) měl být desítkový logaritmus.
A druhá věc: funkce CallCena() se v tom VBA nepočítá obdobně jako PutCena(), ale na konci je tam ještě „- Volatilita * Sqr(ZivotOpce)“, což už by tam podle mě být nemělo.
Je to OK?
Ahoj Michale,
Ad1/ Excelovské a VBA funkce jsou odlišné. LOG ve VBA vrací hodnotu přirozeného logaritmu. Pokud bych chtěl desítkový logaritmus, musel bych přirozený logaritmus přepočíst např. Log(x)/Log(10)…
Ad2/ Ve skriptu Call Ceny je na konci N(d2), kde (d2) se vypočítá jako (d1 – Volatilita * Sqr(ZivotOpce)), je to na stránce příspěvku ten poslední vzorec pod vzorci s výpočtem cen s barevnými obdélníky, skript je podle něj
Jinak děkuji za pozorné čtení, měj se hezky a ahoj, Jirka
Ahoj Jirko,
v první řadě velké díky za zajímavé články a těším se na další :).
Zkusil jsem si modelovat oceňování podle BS modelu, vše funguje, jak má, ale teď přemýšlím, co mi to vlastně ukazuje, jak to použít a interpretovat.
Když se podívám na poslední dny, tak ceny opcí jsou vypočtené z historické volatility pro AAPL jsou vyšší, než vidím v platformě, protože aktuální implikovaná volatilita je nižší (0,30 x 0,18). Dá se nějakým matematickým postupem (nebo jiným modelem?) dostat k implied volatilitě a nemyslím tím teď reversní vyjádření volatility pomocí BS modelu (že zadám cenu opce a vypadne mi volatilita) ani nákupem dat?
Ptám se, protože jsem chtěl na základě vypočtené teoretické ceny opce (a dopočítaných greeks) backtestovat opční strategie – např. jednoduché mechanické vypisování weekly opcí na SPY na základě delty. Bude mi to dávat smysluplné výsledky (prémia), když při výpočtu jejich hodnoty používám historickou volatilitu a ne implied?
Předem díky za odpověď.
Ahoj Romane,
pokud jsem porozuměl otázce správně, tak chceš dostat historické hodnoty Implied Volatility zakomponované do cen opcí? Pokud ano, tak to je právě ta největší výzva pro backtesty opčních strategií, protože jsi vždy v daném okamžiku v minulosti schopen určit cenu podkladu, strike, dobu do expirace, úroky, dividendy a historickou volatilitu. Pak jsi schopen vypočítat cenu opce v každém okamžiku v minulosti na jakémkoliv strike a jakýkoliv podklad, výsledkem ale bude, jaká cena opce měla férově v daný okamžik být (vychází totiž z historické volatility) namísto toho, jaká skutečně byla (neznám totiž Implied Volatilitu v danou chvíli v historii). Budeš schopen tvořit opční řetězce s cenou opcí podle pohybů podkladů, jak se udály před tvým výpočtem (viz výpočet Historické Volatility), ale to bude velmi nepřesné, protože v danou chvíli bude Implied Volatility téměř vždy jinde a a také ceny opcí se budou samozřejmě lišit a někdy může být rozdíl dost dramatický, takže nějaký backtest nebude mít valnou vypovídací hodnotu. Pravděpodobně nebude softwarově náročné vypočítat cenu opce s historickou volatilitou a vytvoření jakéhokoliv teoretického opčního řetězce s takovou férovou cenou, ale pokud budu mít proti tomu také ceny těchto opcí, které se skutečně v daných chvílích objevovaly, tak nebude zase tak softwarově náročné zjišťovat, jestli je férová cena a tržní v nějakém nepoměru, protože to bude způsobovat Implied Volatilita a vysledovaný cenový rozdíl půjde na její vrub.
Prakticky, vypočítal bych, že při ceně AAPL 140 USD před rokem by měla být cena Call opce s expirací 60 dnů na strike 150 na úrovni 320 USD a toto vycházelo z hodnoty 30-ti denní historické volatility, kterou jsem vypočítal na úrovni 16,50% (podle třicetidenních pohybů na AAPL vycházejících z období před výpočtem této ceny). Pohledem na skutečné ceny zjišťuji, že cena této opce ale byla 450 USD, je tak o 40% vyšší než měla být. Mohu pak velmi zjednodušeně říct, že když jsou všechny cenotvorné prvky v danou chvíli stejné (cenu podkladu, strike, dobu do expirace, úroky, dividendy) kromě cenotvorné volatility, tak tato volatilita musí být nikoliv 16,50% ale 23.10% (+40%).
Protože nemám k dispozici data historických Implied Volatilit na všech strike, expiracích atd., musím mít k dispozici alespoň ceny těchto opcí, abych mohl provádět alespoň tato srovnání. Získat takové hodnoty lze buď zakoupením nebo vlastním plněním databáze z nějakých volných zdrojů historických dat (například TOS). Pak se mohu rozhodnout, jestli sesbírám skutečné ceny nebo jenom hodnoty Implied Volatilit nebo obojí. Nutně ale také vzniká otázka, nakolik jsou pak taková data přesná, protože například v TOS (ThinkBack) jsou někdy značné nepřesnosti viditelné pouhým okem.
Tak nevím, jestli je to nakonec to, nač jsi se ptal, pokud ne, tak zkus dotaz nějak konkretizovat, ahoj a měj se, Jirka :c)
Dobrý den, včera jsem porovnával vypočítanou cenu SPY s cenou skutečnou a dostával jsem značně rozdílné hodnoty. U jiných tickerů problém nebyl. Byly to opce s expirací po po 15. červnu (tedy s dividendou). Do výpočtu jsem uváděl dividendu 1,8%. Neví někdo přítomný, kde bych měl hledat chybu?
Díky předem.
Ahoj Pavle,
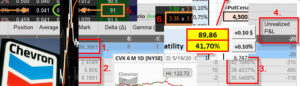
problém asi bude se zadáváním Implied Volatility a v zadání Dividendy. Dividenda je v BSM modelu promítnuta tak, jak jsem ji popisoval v článku, takže nebude mít na konečné číslo podle tohoto Excelu nějaký valný vliv, ale projeví ce v plné částce v hodnotě ITM Put opcí. U Implied Volatility záleží, odkud bereš její hodnoty. Pokud bych se podíval na opční řetězec podle TOS po výplatě Dividendy (jak uvádíš), tak vidím chybně se zobrazující IV z tohoto zdroje, viz obrázek.
Z obrázku vyplývá, že IV u ATM 278 Call opce je 7.39%, kdežto na ATM 278 Put opce je 12.147%, to je téměř jednou tolik!!! Pokud si zobrazím stejný opční řetězec u IB, mám možnost pozorovat následující.
Na obou stranách Call i Put je hodnota IV stejná cca 8.5% resp. 8.6%. Pokud zadáš tyto hodnoty do výpočtu, zobrazí se ti téměř správné hodnoty, pouze u ATM a ITM Put opcí bude připočtena hodnota Dividendy. TOS je prostě nutné brát někdy s rezervou. Ahoj a měj se, Jirka :c)
Děkuji mnohokrát za odpověď a za srozumitelný článek k oceňování opcí. Umíte to názorně vysvětlit. Dříve jsem se prokousával ne příliš „uživatelsky přátelskými“ články. Někde jsem, tuším, četl, že BS model byl oceněn Nobelovou cenou. Zajímavé, že lze Nobelovu cenu udělit v oboru tradingu. S tradingem mám trochu etický problém, že společnosti nic nepřináší. Ale asi nerozumím podstatě této branže. Nobelova cena byla asi udělena za významné matematické vyjádření tržní ceny produktu.
Mohu se zeptat jak se vypořádáváte s volatility skew? V některých analýzách obchodů mně skew výrazněji ovlivňuje výsledky. Předpokládám, že mohu pro konkrétní podklad použít funkci, která skew zohlední ale nevím, jestli se při výraznější změně volatility bude měnit i tato funkce. Zabýváte se tím? Pokud nedostanu odpověď, tak vím, čím toje (dívaje se na časovou strukturu VX futures). Zřejmě čas obchodních příležitostí. Pro mě jsou futures zatím vyšší liga, tak mám čas na dotazy.
Ahoj Pavle, momentálně píšu článek o „šikmosti“ a „špičatosti“ historické volatility – tedy pohybů podkladového aktiva v minulosti, jako volné pokračování posledního článku, takže mám podezření, že jste se mi naboural do počítače :c) Chci ukázat, jak se skewness a kurtosis na těchto historických pohybech měří a jaké si z tohoto měření mohu vyvodit závěry pro budoucí obchody. Skewness na volatilitě (vertikální i horizontální) a využití jejich poruch je hlubší téma, ale je základem dobrých opčních obchodů, k ní se určitě v nejbližší době dostanu. Pokud pozorujete časovou strukturu VX futures, tak tady je pozorování očekávané volatility alfou a omegou celého podniku, protože tvoří poruchy v časové struktuře a vyrábí obchodní příležitosti na těchto nástrojích. Ahoj, Jirka :c)
Děkuji za odpověď. Těším se na další článek.
Dostal jsem zajímavý e-mail od čtenáře Pavla, jehož část bych si dovolil zde uveřejnit „…Pro analýzy obchodů používám funkce z Vašeho xls souboru teoopt (děkuji). Skew mně ale podstatně ovlivňuje některé analýzy. Do souboru jsem doplnil funkci, která IV skew zohledňuje. Je to jenom první pokus a „volatility smile“ není dokonalý (hlavně u vyšších strikes). To by šlo ovšem doladit pomocí dalších funkcí. To zatím nepotřebuji, protože přesnost cen pro ne příliš vzdálené strikes je naprosto postačující. Skew pro různé tickery dolaďuji dvěma parametry. Není to nic převratného ale analýzy se zohledněním skew jsou podstatně přesnější.…“ Pavlův soubor s excelem a scriptem funkce pro hloubavé povahy je možné nalézt zde výpočet skew :c)
Ahoj,
chtěl bych zareagovat na následující větu:
„Pominu nyní vliv nabídky a poptávky na cenu opčního kontraktu a pokusím se jednoduše ukázat, bez nějakého „vědeckého podtextu“, jak jsou takové ceny stanoveny.“ Jak moc má teda na cenu opce vliv nabídka a poptávka? Vychází cena pouze z BS modelu? Nebo cenu nabídka a poptávka nějakou ovlivňují?
Dále bych se zeptal, zda jsem pochopil správně, že první se nějaký super výpočtem vypočítá IV a pak se tato hodnota dosadí do BS modelu a vyjde cena opce? Nebo se nejprve dostane cena opce (na základě nabídky a poptávky) a z ní se pak vypočítá přes BS model Implikovaná volatilita?
Díky moc za odpověď
Ahoj,
jestli cena vychází z BS modelu takového, jak jde jeho výpočet nalézt v každé lepší knize o opcích, tak to opravdu nevím. Když jsem se pokoušel přečíst a pochopit knihu Volatility Smile (viz Recenze), tak o takovém „surově jednoduchém“ způsobu pochybuji. Tvůrci a organizátoři trhů mají bezpochyby sofistikovanější algoritmy, než je ocenění BS modelem nebo přinejmenším používají jeho všemožná vylepšení, nicméně někdo opravdu musí cenu, tak jak ji vidím v platformě, nastavit a nabízet. Výpočet Implied Volatility je klíčem k výši ceny, to jsem popisoval mnohokrát, dalo by se říct, že Cena je funkcí Volatility – vyšší volatilita = vyšší cena a naopak. Pokud bych se dnes (v dubnu) zeptal tvůrce trhu, jakou mi nabídne cenu opčního kontraktu SPX s expirací příští rok v říjnu, tak nepochybně do svého výpočtu vloží (mimo jiných věcí, které jsou mu přesně známé) hodnotu Implied Volatility na úrovni cca 20%, protože to je její průměrná a běžná hodnota a nemůže nyní vědět, co se bude na trzích dít za jeden a půl roku a takto vygenerovanou cenu podle této IV mi pak nabídne. Postupem času však na cenu této opce bude mít vliv jednak poptávka a nabídka po opcích na tomto strike a samozřejmě také události, které budou formovat tržní náladu kolem tohoto titulu. Nepříjemné události patrně zvednou cenu této opce díky nabídce a poptávce a také z důvodů, že „jiné výpočty“ budou účastníkům trhů říkat, že IV na úrovni 20% je nyní zcela mimo realitu, což mohou například ukazovat nejčerstvější pohyby na podkladu, ze kterého je opční kontrakt odvozen, patrně budu mít lepší odhad rozptylu ceny do expirace za čtrnáct dnů než při expiraci za rok a půl. V odkazu na výše uvedenou knihu pak tato pojednává ve valné části právě o modelování samotné volatility, abych mohl usuzovat, jestli je nyní dobře do ceny započtena nebo nikoliv. Z tohoto pohledu a přístupu je pak také patrné, proč je IV „skewed“ horizontálně – tedy liší se pro každou jednotlivou expiraci.
Takže ve shrnutí, nejdříve je na základě nějakého výpočtu cena opravdu vypočtena nějakým matematickým modelem, následně je ale korigována působením trhů a chováním jejich účastníků, nebudu nyní patrně nabízet ATM Long Call 100 za 500 USD pro podkladovou akcii, která má hodnotu 100 USD a je schopna do expirace za deset obchodních dnů udělat +/- 15 USD pohyb, ale bude patrně nabízena za zhruba 1500 USD…k tomuto zjištění mi patrně bude sloužit nějaká výpočetní metoda pozorující aktuální a nejblíže minulé chování ceny. Pokud tedy vím, že cena 500 USD za tuto hypotetickou opci představuje IV na hodnotě modelově 18%, pak bude pro aktuálně nabízenou cenu 1500 USD představovat IV na úrovni například 54%…:c)