Lepší okamžik pro napsání tohoto článku jsem si ani nemohl přát. Lehké náznaky bankovní krize vyplývající z podivné likvidity speciálních bankovních domů opepřené komentáři jejich více či méně schopných představitelů přinášejí na přelomu měsíce března a dubna 2023 skvělý rámec pro téma tohoto článku. Jakou roli v této šlamastyce sehrály základní vlastnosti dluhopisů bude předmětem následujících řádků.

   Rostoucí úrovně úrokových sazeb znamenají pro dluhové cenné papíry s pevným výnosem pokles jejich ceny a naopak, poklesy hodnot úrokových sazeb na trzích znamenají pro tyto cenné papíry růst jejich aktuálních cen. Obě tyto závislosti již byly v dosavadních článcích o dluhopisech popsány s naznačením, co by mohlo tyto závislosti vysvětlovat. Pokud jsem tedy držitelem dluhopisu, bude mě především zajímat, jak takovou skutečnost kvantifikovat, jak určit míru závislosti pohybu úrokových sazeb na ceně drženého dluhopisu a případně, jaké nástroje k tomu mohu využít. Základní pochopení těchto „měřících nástrojů“ pak může být dobrým základem pro jejich správnou interpretaci a může také spoluvytvářet rozhodnutí, kdy do těchto dluhových cenných papírů vstoupit a jaké si k tomu vybrat.

   V předchozích článcích jsem popisoval mou konkrétní investici, kterou mám na svém obchodním účtu, a to investici do pětiletého dluhopisu Ford s kupónem 6.625% p.a. a se splatností 15.2.2028, využiji tak pro ukázku závislosti ceny a výnosu dluhopisu opět tento konkrétní dluhopis. Mohu pozorovat, na obrázku níže, jeho aktuální cenové parametry.

   Aktuálně bych byl schopen nakoupit tento dluhopis za cenu 1.024,73 USD. Nyní už vím, že investice do tohoto dluhopisu by představovala výnos do splatnosti 5.838% p.a., tento výpočet jsem popisoval v článku Dluhopisy – V., když při jeho výpočtu jsem vycházel z excelovské tabulky, kterou jsem si pro tento účel vytvořil. Tento výpočet je na obrázku níže.

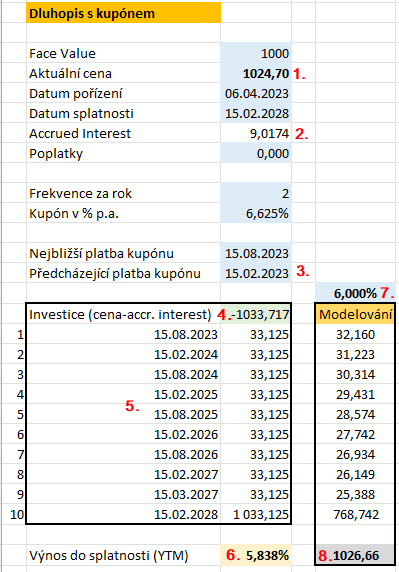
   Pro připomenutí, co vlastně na obrázku mohu vypozorovat, upozorním na základní momenty tohoto výpočtu. Aktuální cena 1.024,70 USD (1) musí být zatížena částkou -9.0174 USD (2), která představuje úroky, které mi nepatří a budou mi sraženy v případě, že bych opravdu tento dluhopis nyní nakoupil a představují naběhlé úroky z kupónu za dobu od jeho poslední výplaty dne 15.2.2023 (3) do dne, kdy si jej pořídím. Musím tak svou investici upravit na patřičnou cenu ve výši -1.033,717 USD (4), která je součtem pořizovací ceny a tohoto „mě nenáležejícího“ úroku. Mohu pak pozorovat, že mě v budoucnu čeká deset peněžních toků (5), kupónových výplat, kdy poslední kupónová platba je doprovázena splátkou Face Value dluhopisu. Excel mi vypočítá výnos do splatnosti (YTM) ve výši 5.838% p.a. (6). Mohu pak přistoupit k jednoduchému modelování a pomocí diskontování budoucích cash flow z dluhopisu podle mnou zadaného požadovaného výnosu (7) chtít zjistit, jaká by byla jeho aktuální cena. Konkrétně, pokud bych požadovat výnos do splatnosti ve výši 6% p.a., musel bych být schopen nakoupit dluhopis za částku 1.026,66 USD (8), tedy musel bych jej pořídit zhruba o šest dolarů levněji než nyní. U tohoto modelování nyní zůstanu.

   Nabízenou možnost modelovat a následně prozkoumat vývoj ceny dluhopisu v závislosti na požadovaném výnosu jsem využil pro zjištění tohoto chování na škále požadovaného výnosu v rozmezí od -3% p.a. až po +50% p.a. a výsledek takového zkoumání jsem si nechal zobrazit graficky, níže je výsledek:

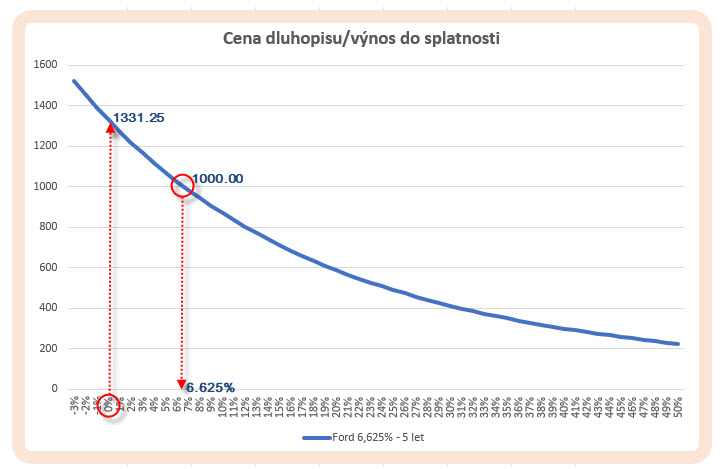
   Pravděpodobně v každé publikaci nebo obecném článku o dluhopisech budete moci spatřit takto podobně vykreslenou závislost ceny dluhopisu na jeho výnosu. Co bude pro tuto chvíli stěžejní, je poznání základní charakteristiky této křivky, a to konstatování, že její tvar je konvexní.  Není to tedy žádná lineární závislost, nicméně vykreslený tvar napovídá, že s růstem požadovaného výnosu dluhopisu (zleva doprava) klesá jeho cena a naopak. Mohu pak nyní na této křivce vyznačit alespoň dva „kritické body“, které by mě mohly v tuto chvíli zajímat.

   1/ Hodnotě 0% výnosu odpovídá cena dluhopisu ve výši 1.331,25 USD. Co to znamená? Výpočet výnosu do splatnosti (článek Dluhopisy – V.) vychází z úvahy, že pořízení kupónového dluhopisu za určitou cenu (v mém případě 1033,717 USD) s určitým kupónem (v mém případě 6.625% p.a.) bude představovat určitý vypočítaný výnos do splatnosti (v mém případě 5.838% p.a.) za splnění předpokladu, že všechny kupónové platby budu v budoucnosti reinvestovat právě s vypočítanou úrokovou sazbu 5.828% p.a., potom mohu s takto vypočítaným výnosem opravdu počítat (neberu v úvahu předčasné svolávání emise – Call). Pokud bych se ovšem rozhodl, že tento pětiletý dluhopis Ford 6.625% nakoupím a žádné reinvestice kupónů provádět nebudu, nesmím jej koupit za cenu vyšší než je cena 1.331,25 USD, protože právě tato cena představuje součet všech budoucích plateb kupónů a splacení Face Value tak, abych obdržel alespoň původní investici ve výši 1331,25 USD zpět. Konkrétně: -1.331,25 USD pořizovací cena dluhopisu + (10*kupón ve výši 33.125 USD) + (1.000 USD Face Value u maturity) = -1.331,25 + 331,25 USD + 1.000 USD = 0.   

   2/ Hodnotě 6.625% výnosu odpovídá cena dluhopisu ve výši 1.000,00 USD. Pokud se rovná požadovaný výnos dluhopisu hodnotě jeho kupónu (6.625% p.a.), měla by být jeho cena rovna hodnotě Face Value. Tento výnos do splatnosti je tak hraničním bodem, kde se láme cena dluhopisu vzhledem ke své Face Value, výnosy vyšší než vyznačený kupón znamenají cenu nižší než je Face Value a naopak, výnosy nižší než vyznačený kupón znamenají cenu vyšší než je Face Value.

Stejný dluhopis – jiný kupón

   Aktuální úrokové sazby se mění na trzích neustále a stejně tak se promítají do ceny dluhopisů, jejich ceny odpovídajícím způsobem fluktuují a odrážejí tak jejich aktuální výši. Přestože se do ceny dluhopisů promítají další cenotvorné prvky, například doba do splatnosti dluhopisu nebo kreditní riziko popisované v minulém článku, je vliv úrokových sazeb na jejich cenu zásadní a zaslouží si více mé pozornosti. Mohu tak nyní modelování rozšířit na pozorování, jak by vypadalo působení této změny úrokových na cenu dluhopisu v případě, že budu srovnávat dluhopisy se stejnou dobou splatnosti a stejným aktuálním výnosem, pouze se budou lišit velikostí vyznačeného kupónu. Konkrétně srovnám můj nakoupený pětiletý dluhopis Ford s kupónem 6.625% s fiktivním dluhopisem Ford se stejnou dobou do splatnosti, tento by měl však kupón pouze 2.00 % p.a. Na obrázku níže srovnání obou křivek – původního dluhopisu s kupónem 6.625% a dluhopisu s nižším kupónem.

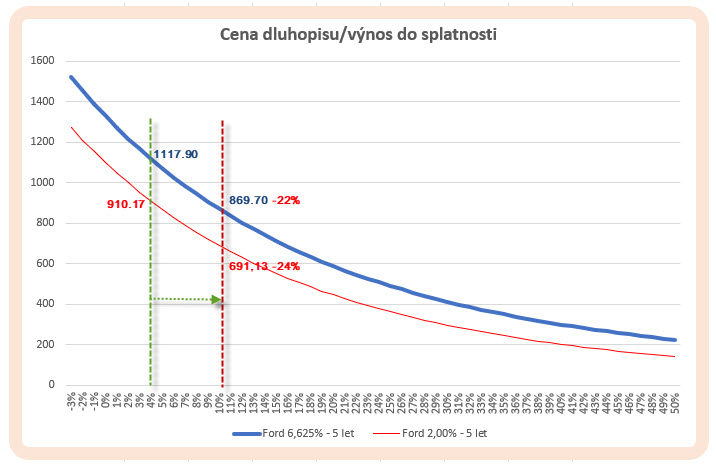
   Pětiletý dluhopis s kupónem 6.625% (modrá křivka) s aktuálním výnosem 5.838% by dnes stál 1.033,717 USD (s připočítanými náklady na úrok, který mi nepatří), stejný pětiletý dluhopis se stejným požadovaným výnosem 5.838% ovšem s kupónem pouze 2% p.a. by pak musel stát mnohem méně a protože požadovaný výnos je vyšší než jeho kupón, musí jeho cena být silně pod Face Value. Aktuálně bych jej pořídil za 832.90 USD. V provedené simulaci pak bude křivka mapující změnu ceny s ohledem na výnos (červená křivka) na nižších úrovních, bude však mít mírně jiný sklon. Na obrázku jsem vyznačil pohyb úrokových sazeb z hladiny 4% na 10%. Mohu pak pozorovat, že oba dluhopisy ztratí na své ceně, každý ale jinak. Dluhopis s vyšším kupónem 6.625% p.a. ztratí z ceny 1117.90 hodnotu 248.20 USD a jeho cena bude o -22% nižší a bude na úrovni 869.70 USD. Dluhopis s nižším kupónem 2% p.a. spadne z ceny 910,17 USD připadající na 4% p.a. výnos na úroveň 691.13 USD představující výnos 10% p.a., tento pokles o -219.04 USD ale představuje -24%. Mohu nyní konstatovat (popsat další vypozorovanou vlastnost), že stejné dluhopisy se stejnou splatností a aktuálním výnosem nebudou reagovat na změnu úrokových sazeb stejně, náchylnější na změnu ceny budou dluhopisy s nižším kupónem. Čekám zvýšení úrokových sazeb a chci nakoupit dluhopisy, pokud budu chtít vybírat mezi dluhopisy se stejnou splatností, měl bych se zaměřit na ty s vyšším kupónem, jejich cenový pokles v souvislostí se zvýšení úrokových sazeb nebude tak silný, jako u stejného typu dluhopisu s nižším kupónem. Očekávání snížení úrokových sazeb by mělo doprovázet opačné rozhodnutí.

Stejný dluhopis – jiná splatnost

   Rozhodování o pořízení dluhopisu v souvislostí s očekáváním pohybu úrokových sazeb aplikované na dluhopisy se stejnou kvalitou, stejnou dobou do splatnosti a stejným aktuálním výnosem ale s přihlédnutím k jiné výšce kupónu mohu obohatit o další rozhodovací proces. Mohu srovnat původně nakoupený pětiletý dluhopis Ford s kupónem 6.625% s fiktivním dluhopisem se stejným kupónem, ovšem se splatností deset let, tedy dvojnásobnou délkou do maturity. Na obrázku níže graficky znázorněná závislost ceny dluhopisu na změně výnosu.

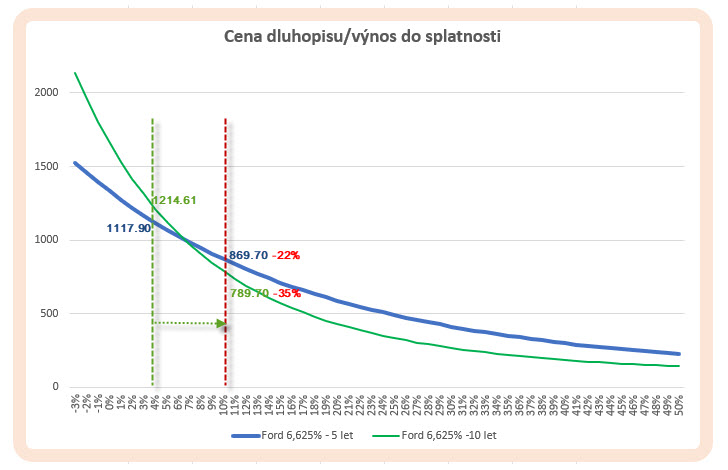
   Na první pohled je jisté, že mezi křivkami znázorňující citlivost ceny dluhopisu na změnu výnosu má strmější charakter křivka identicky kvalitního dluhopisu se stejným kupónem a aktuálním výnosem lišícím se pouze délkou splatnosti (zelená křivka). Mohu pak provést obdobnou simulaci pohybu úroků z hladiny 4% p.a. na úroveň 10% p.a. a pozorovat, jak se změní ceny těchto dluhopisů. Původní pětiletý dluhopis Ford s kupónem 6.625% ztratí při takovém pohybu úrokových sazeb -22% své ceny, to se oproti simulaci výše v odstavci nezměnilo. Identický dluhopis, ovšem s dvojnásobnou dobou do splatnosti, však ztratí ze své ceny 1214.61 USD vypočítané pro výnos na úrovni 4% p.a. částku -424.91 USD, protože cena tohoto desetiletého dluhopisu při výnosu 10% p.a. bude pouze 789.70 USD, tento pokles ceny pak představuje značných -35%. Mohu tak definovat další obecné pravidlo pro rozhodování o nákupu dluhopisu spojené s očekáváním pohybu úrokových sazeb na trzích. Očekávám-li další růst úrokových sazeb a vybírám mezi stejně kvalitními dluhopisy se stejným kupónem, u dluhopisu s delší dobou splatnosti mohu očekávat jeho významnější snížení ceny než u stejně kvalitních dluhopisů s kratší dobou do splatnosti, obdobně samozřejmě opačná úvaha s očekáváním poklesů úrokových sazeb.  

Durace

  Poznání, že cena dluhopisu je funkcí jeho výnosu, umožňuje „zmatematizování“ této základní poznané závislosti. Pokud jsem mohl na tomto webu na spoustě míst zkoumat, jak se mění cena opčního kontraktu v závislosti na ceně podkladu pomocí řeckého písmene Delta, mohl bych se pokusit zjistit, jakým způsobem je matematicky popsáno toto základní chování změny jeho ceny v závislosti na změně úrokových sazeb u dluhopisu. V článku Delta Neutral – VI. jsem v úvodu matematické úvahy o změně ceny opce v závislosti na změně ceny podkladu definoval tento pohyb jako první derivaci cenové funkce této vlastnosti změny ceny opčního kontraktu. Pokud jsem tedy schopen nalézt takovou funkci popisující vztah závislosti změny ceny na změně argumentu – úrokové sazby, musí existovat matematické vyjádření, jak tento vztah zachytit. Výše uvedené obrázky, které zachycovaly nejzákladnější simulace vztahu ceny a výnosu nejsou ničím jiným než zobrazováním cenových funkcí nejrůzněji definovaných dluhopisů v závislosti na změnách úrokových sazeb, tedy aktuálního výnosu odvíjejícího se od aktuální úrokové sazby na dluhopisových trzích, každá modelovaná změna výnosu přinesla jinou cenu každého konkrétního dluhopisu, kterou zachycovaly jednotlivé křivky zobrazené v grafech. Bylo na obrázcích patrné, že každá z křivek funkce ceny v závislosti na výnosech má jinou „strmost“ podle zadaných vlastností dluhopisů, tuto strmost pak lze matematicky měřit. Zjištění vlastnosti úhlu, který svírají tečny k těmto křivkám v každém konkrétním bodě, který potřebuji, je právě klíčem k hledání odpovědi, jak veliká je závislost ceny dluhopisu na pohybu úrokových sazeb. Na obrázku níže je patrné, jak je to myšleno:

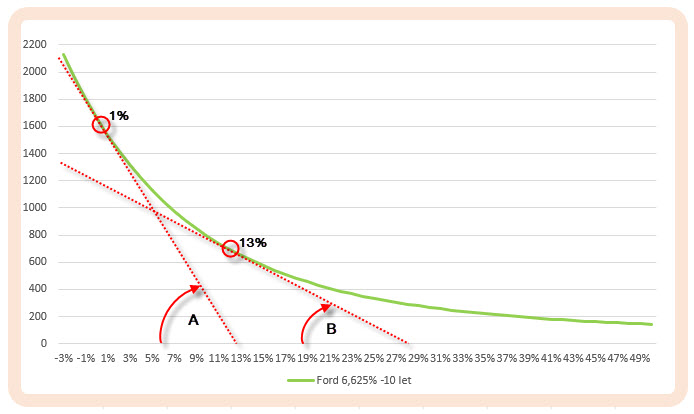
   Zjevně vyšší strmost a také úhel A svírá tečna k cenové křivce a osa „x“ pro dluhopis Ford 6.625% se splatností 10 let pro výnos 1% p.a. než je strmost a úhel B tečny pro výnos představující 13% p.a., je pak jasné, že v oblastech s vyšší strmostí se budou ceny dluhopisu v závislosti na výnosu měnit dramatičtěji než v oblastech s nižší strmostí a toto umí matematika zachytit. K vyhodnocení strmosti (jejího úhlu) musíme znát tvar cenové funkce se kterou nakládáme, a pokud ji tedy budeme znát, bude nám stačit mít povědomí o derivování a máme vyhráno :c).     

   Cenovou funkci pro výpočet aktuální ceny kupónového dluhopisu známe z předešlých článků, je uvedena na obrázku níže: 

   Aktuální cena dluhopisu SH je součtem všech budoucích peněžních toků, které mi pořízený dluhopis přinese diskontovaných příslušným úrokovým výnosem úrok. Každá budoucí kupónová výplata C a závěrečná splátka Face Value FV vstupuje do tohoto součtu s předpokladem jejího reinvestování za příslušnou úrokovou sazbu úrok, hodnota n – je počet period, které tyto budoucí peněžní toky přinesou. Derivováním této cenové funkce mohu zjistit, jak se změní cena dluhopisu s přihlédnutím ke změně jeho výnosu:  

   Zkoumáním této první derivace funkce ceny dluhopisu je možné posuzovat vliv výnosu – úrokové sazby na jeho cenu, tedy zkoumat vlastnosti této derivace cenové funkce podle aktuálního výnosu – hodnoty úrok v derivované rovnici. Kanadský ekonom a matematik Frederic Macaulay, aby mohl posoudit tuto derivaci podle aktuální ceny dluhopisu SH, provedl v této derivované rovnici úpravu vydělím obou stran rovnice právě současnou hodnotou SH dluhopisu a navíc v rovnici na pravé straně vytkl výraz 1/(1 + úrok) před závorku. Rovnice po úpravě pak vypadala takto: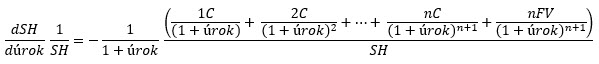    

   Z derivované rovnice je zajímavá její část na pravé straně rovnice označena níže:

   Činitel – zlomek na pravé straně rovnice (červený rámeček), kde dělitelem je současná hodnota dluhopisu, se nazývá Macaulayova Durace, potom „čistěji“ zobrazeno:

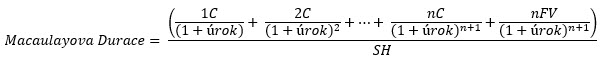
   Macaulayova Durace představuje vážený průměr splatnosti všech budoucích peněžních toků z pořízeného dluhopisu, kde vahami jsou právě tyto peněžní toky. Mohu totiž ze zlomku vypozorovat, že se jedná o součet všech diskontovaných plateb kupónů a závěrečné výplaty Face Value, což již běžně dělám ve svém excelu ke zjištění výnosu do splatnosti, pouze je každý tento tok obdařen vynásobením „pořadím“, kdy tento peněžní tok nastane (v čitateli 1C, 2C…nC, nFV). Z tohoto pohledu, přestože to zní dost nepochopitelně a nepředstavitelně, Macaulayovu Duraci lze velmi jednoduše vypočítat a využít ke zjištění toho, co jsem od svého teoretizování vlastně potřeboval, tedy zjistit, jakým způsobem se mi změní cena dluhopisu, pokud se změní úroková sazba o nějakou předem danou hodnotu, například o +/-1%. Stejně jako u řeckého písmene Delta, která postihovala vyjádření změny ceny opčního kontraktu, pokud se změní cena podkladu o +/- 1.00 USD, bude mě to samé zajímat u dluhopisů. Dosadím tedy výraz Macaulayova Durace do původní derivované rovnice:  

  Výsledná rovnice pak vlastně znamená vydělení Macaulayovy Durace právě aktuálním výnosem a takto upravené Macaulayově Duraci se říká Modifikovaná Durace, matematicky tedy po úpravě, aby to bylo zřetelnější:

   Poměřením Macaulayovy Durace s aktuální úrokovou sazbou obdržím přesně to, co pro své potřeby potřebuji, normalizaci pohybu ceny dluhopisu k nějaké hodnotě výnosu, tedy výpočet změny ceny dluhopisu, pokud se změní úrokové sazby o +/-1% bod. Z nastíněného postupu, byť se může zdát komplikovaný a složitý, mohu obě durace pro jakýkoliv dluhopis velmi jednoduše vypočítat, což také udělám pro svůj dluhopis Ford s kupónem 6.625% a se splatností za pět let a pokusím se svůj výpočet interpretovat.

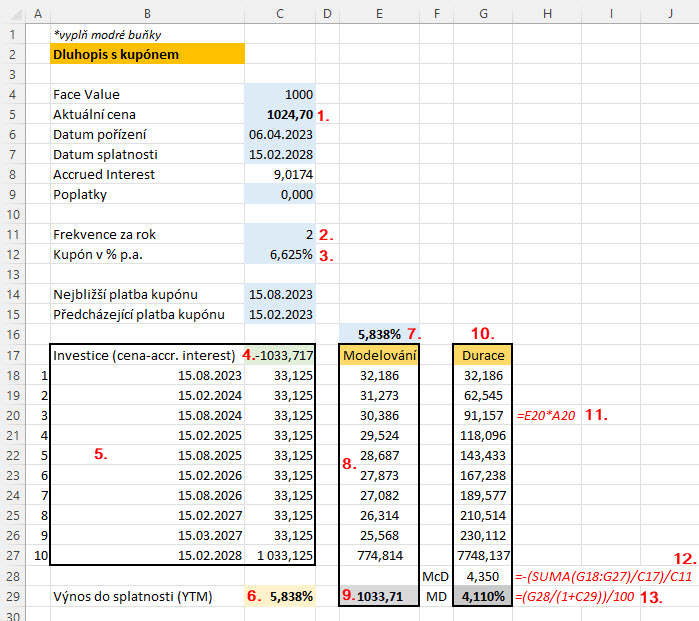
   Pokud bych dnes nakoupil pětiletý dluhopis Ford za 1.024,70 USD (1), který vyplácí pololetně (2) kupón ve výši 6.625% p.a. z Face Value (3), potom by celá investice představovala částku 1.033,717 USD (4), protože bych musel z prvního kupónu odevzdat jeho část předcházejícímu držiteli. Deset peněžních budoucích toků (5) by představovalo při daných pořizovacích podmínkách výnos do splatnosti ve výši 5.838% p.a. (6). V části výpočtu „Modelování“ při zadání stejného výnosu ve výši 5.838% p.a. (7) mohu pozorovat všechny budoucí toky diskontované k dnešnímu dni právě podle této úrokové sazby (8) a jejich součet (9) mi musí dát (pro kontrolu správného diskontování) přesně součet představující aktuální pořizovací cenu (4). Ve sloupci „Durace“ (10) mohu vypozorovat, že jsem diskontované peněžní toky ze sloupce „Modelování“ vynásobil vahami jejich pořadí (11), tedy například pro třetí peněžní diskontovaný kupón ve výši 30.386 USD jsem tuto hodnotu vynásobil trojkou. Takto „zvážené“ peněžní toky jsem sečetl a vydělil skutečnou pořizovací cenou zkoumaného dluhopisu v buňce C17 (12), tím jsem vypočítal hodnotu Macaulayovy Durace, protože je ale kupón vyplácen 2x za rok, vydělil jsem tuto duraci ve vzorci dvěma (hodnotou z buňky C11). Průměrná vážená doba splatnosti všech peněžních toků je pro můj dluhopis 4.35 let. To je sice hezké, ale já jsem ještě hodnotu Macaulayovy Durace vydělil aktuálním výnosem ve výši 5.838% (13), abych se dobral hodnoty Modifikované Durace ve výši 4.110%. To je jednoduchý konec mé, na první pohled složitě popisované práce. Co mohu pro toto číslo konstatovat?

   Pokud se zvednou úrokové sazby na trzích o +1% p.a., poklesne hodnota mého pětiletého dluhopisu Ford s kupónem 6.625% o -4.110%, tedy o více než čtyřicet dolarů. Pokud by úrokové sazby měly o -1% klesnout, mohl bych přihlížet růstu ceny mého dluhopisu o přibližně stejnou částku.

Není to tak složité…

   Přestože je výpočet durace velmi jednoduchý pomocí excelu, kde máme vypočítán například výnos do splatnosti s předpřipravenými diskontovanými budoucími cash-flow, je velmi komfortním zjištěním, že obchodní platformy údaje o duraci nabízejí pro každý kvalitnější dluhopis. Mohu pak z mé platformy TWS od Interactive Bokers prozkoumat uváděnou duraci pro můj pětiletý dluhopis Ford.         

   Mohu vypozorovat, že má obchodní platforma ukazuje výnos do splatnosti (YTM) ve výši 5.921% (namísto mnou vypočítaných 5.838%), tedy o pouhou desetinku vyšší (1), hodnota Durace je pak v mé platformě na úrovni 4.21%, namísto mnou vypočítaných 4.11%, tedy o stejnou desetinku vyšší (2). Mohu spokojeně konstatovat, že na výpočet Durace se mohu plně spolehnout a nemusím pro její stanovení používat žádné vlastní pomůcky a hledání její aktuální výše výrazně komplikovat.    

   Pokud jsem výše v článku ukazoval modelování různých vlastností stejných dluhopisů, mohu pak toto modelování promítnout také do hodnoty durace. Pokud budu tedy uvažovat o pořízení dluhopisů se stejnou kvalitou a stejnou dobou do splatnosti, dluhopisy s nižším kupónem budou citlivější na změnu úrokové sazby a budou mít také vyšší (modifikovanou) duraci, toto bych pak mohl demonstrovat na obrázku níže:

   Tři dluhopisy se splatností v únoru 2028 mají každý jinou výši kupónu, s klesající výši kupónů se ale zvyšuje senzitivita na pohyb úrokových sazeb, proto s klesajícím kupónem durace roste.

    Obdobně jsem výše ukazoval, že pokud mají dluhopisy přibližně stejnou kvalitu a stejný kupón, potom jsou na změnu hladiny úrokových sazeb citlivější dluhopisy s delší dobou do splatnosti a tyto dlouhodobé dluhopisy mají také vyšší duraci.

    Na obrázku jsou dva americké vládní dluhopisy s přibližně stejným kupónem (6.125% a 6.25%) ovšem jeden má splatnost v listopadu 2027 a druhý v květnu 2030. Durace dluhopisu s delší dobou splatnosti je na hodnotě 5.86%, dluhopis s kratší dobou splatnosti má duraci 4.03%, rozdíl +/-1.03% v duraci ale představuje téměř o čtvrtinu vyšší riziko pohybu ceny dluhopisu s delší dobou splatnosti oproti dluhopisu s kratší dobou splatnosti v případě zvýšení úrovně úrokové sazby o +1%.

  Aktuálně k duraci :c)

   Vrátím se k poznámce z úvodního odstavce tohoto článku, kdy jsem podotkl, že je opravdu vhodná doba pro téma tohoto článku z pohledu aktuálního dění na trzích, zejména v bankovním sektoru. Jak si mohu ve světle výše napsaných řádků vysvětlit nynější potíže některých amerických bankovních domů, které utrpěly významné ztráty z cenných papírů s fixním výnosem související s problémy jejich likvidity? Nemohu si nevšimnout, že před rokem (do roku 2021) nenabízely například třicetileté americké vládní dluhopisy nijak významné výnosy, tyto se pohybovaly okolo 2% p.a.

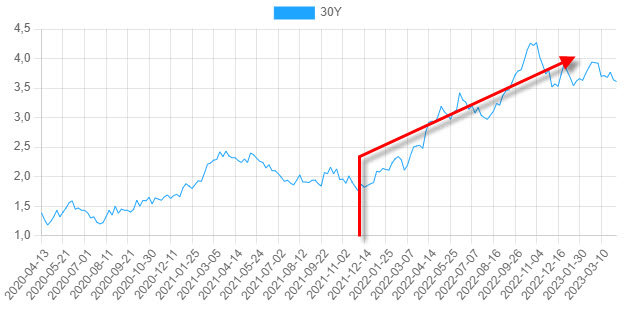
   V atmosféře nízkých výnosů jsem jako fiktivní bankéř spravující peněžní prostředky z vkladů svých klientů nucen tyto vklady nějakým bezpečným způsobem zhodnocovat, proto se jeví nakoupení bezrizikových amerických vládních dluhopisů se splatností třicet let jako vhodná investice. Trhy těchto cenných papírů jsou dostatečně likvidní, mohu tak kdykoliv tyto vládní bondy přetavit zpět na hotové peníze, pokud bych tyto hotové peníze potřeboval. Mohu také prozkoumat, jakou mají tyto dluhopisy duraci, abych zjistil, co se může stát, pokud by centrální banka začala při ekonomických problémech navyšovat úrokové sazby. Na obrázku níže je pro příklad jeden z takových dluhopisů vyobrazen.     

    Třicetiletý americký vládní dluhopis se splatností v listopadu 2050 má modifikovanou duraci závratných 20.71%. Zvýšení úrokové sazby o +1% bod bude znamenat ztrátu ceny těchto dluhopisů o jednu pětinu, a to je velmi zásadní zjištění. Jak víme, ke zvyšování úrokových sazeb nakonec došlo a v letošním roce (2023) dokonce zcela zásadním tempem, které je také znázorněno na obrázku s vývojem výnosu třicetiletého dluhopisu výše. Dluhopisová portfolia s vysokou durací, tedy zejména taková, která obsahují dluhopisy s dlouhou dobou splatnosti, začínají v takovém případě ztrácet na své hodnotě a „vypalují“ tak díry do rozvah ústavů, které je pořídily. Nakonec tuto již tak vážnou situaci zkomplikují vkladatelé, kteří na sociálních sítích zjišťují, že jejich vklady u některých bankovních institucí mohou být v ohrožení a je jim doporučeno, aby své peníze vybrali. Run na banku je tady. Namísto toho, aby manažeři bankovních dluhopisových portfolií se stoickým klidem vyčkali snížení úrokových sazeb a návratu ceny jejich dluhopisů na úrovně, kde byly před zásahy FEDu, musejí tyto organizace vyplácet vklady klientům, kteří si pro ně v rozčilení přiběhli. Ve snaze nalézt pro tyto masové výběry potřebnou likviditu, musejí vyprodávat tato dluhopisová portfolia, tím ale jen stvrzují ztráty, které na nich utrpěly, bankovní apokalypsa u těch z nich, které s takovými pohyby na úrokových sazbách nepočítali, je dokonána. Na své si pak přijdou nejrůznější analytici a odborníci, kteří budou spílat bankovním manažerům, že se na takovou situaci nepřipravili, když investovali zejména do dluhopisů s vysokou durací. Co na to říct? Nikdy nemůžu vědět, co se stane za týden, natož za deset let, co bych pak měl dělat nyní? Nakupovat dluhopisy s vysokou durací, protože je jisté, že úrokové sazby klesnou a já inkasuji profit z růstu jejich ceny?

   Je užitečné mít povědomí, co se může stát, když se úrokové sazby dají do pohybu, pokud jsem tedy dluhopisový obchodník. Nemusím ale provádět složité výpočty, stačí mít povědomí o jednoduchých ukazatelích a nástrojích, které mi dá k dispozici má obchodní platforma současně s jejich správnou interpretací. Mohu pak odhadovat, co se s mými dluhopisy stane, pokud se změní nálada na trzích úrokových sazeb, tedy jak postihne mé dluhopisové portfolio risk změny úrokových sazeb popisovaný v minulém článku.

   Excel s výpočtem durací je možné stáhnou v Diskuzním fóru ve vlákně k tomuto článku, stejně tak zde můžete přidávat své komentáře :c)