Volatilita a Cenový pohyb – I.

   Načerpané poznatky z článku Cena opce mi sdělují, že již vím, z čeho je složen výpočet ceny opčního kontraktu, respektive, které hodnoty do tohoto výpočtu vstupují. Tak již vím, že Hodnota Strike, Délka života opčního kontraktu, vyplácená Dividenda a momentální Úroková míra jsou hodnoty, které mohu přesně kvantifikovat a které tvoří „poznatelnou“ část výpočtu konkrétní opční ceny, toto platí také pro modelování opční ceny do budoucnosti. Jednoduše jsem schopen pro každý budoucí moment přesně stanovit, pro každou z těchto uvedených komponent její přesnou hodnotu. Tato přesná matematická predikce se však netýká budoucí Ceny podkladu a Implied Volatility, zbývajících dvou cenotvorných složek vstupujících do výpočtu opční ceny v každém jednotlivém okamžiku. Takto poznaný problém by pak mohl formulovat samotnou podstatu opčního obchodování, tedy že opční trading je založen především na poznání interakci ceny opce na pohybu Ceny podkladu a vývoji Implied Volatility.  

   Nedělám si pražádné ambice vytvářet predikce budoucího pohybu ani jedné ze dvou těchto cenotvorných složek – Ceny podkladu nebo Implied Volatility. Po létech strávených tradingem jsem musel vyhodnotit, že mé vlastní vytváření jakýchkoliv přesných prognóz v tomto směru je nejen nemožné, ale hlavně zcela zavádějící a zejména znamená plýtvání drahocenným časem. Jednoduše jsem vyhodnotil, že finanční svět okolo mě se nepohybuje tak, jak bych si přál a jak jsem mu ve své hlavě předurčil, ale že funguje zcela nezávisle na mém vědomí, bytí a obchodování. V žádném případě to ale neznamená, že jsem úvahy na toto téma ze svého obchodování zcela vypustil, ba naopak, stala se předmětem dosti bedlivého zkoumání a vyhodnocování a zcela zásadní a nepostradatelnou nezbytností, pouze se necítím být povolán k tomu, abych někomu drze tvrdil, že cena akcie Tesla Inc. bude příští týden v pátek na hodnotě 321.40 USD a že Implied Volatilita opcí na ATM strike akcie Facebook bude příští středu pro opční řetězec expirující za měsíc na úrovni 31%. Budoucí cenový pohyb na podkladu a Implied Volatilita jsou spojité nádoby a jsou navzájem logicky, prakticky i matematicky propojeny, ale jejich přesnou predikci bych si pro svou komplexnost a neurčitost nedovolil. 

   K vytvoření nejjednodušší představy o možných budoucích pohybech podkladového aktiva (budu mít v celém článku na mysli akcie, pro jiné podklady to pak samozřejmě platí obdobně) mi nezbude nic jiného, než usuzovat z pohybu minulých. Nemohu se spoléhat, že budoucí poznané předpoklady možného cenového pohybu – významná politická událost, špatná předpověď počasí, vojenský konflikt, vyhlašování hospodářských výsledků, výplata Dividendy, odvolání správní rady, schválení výroby léku, vynesení rozsudku v neprospěch společnosti a podobné zprávy, budou mít měřitelný vliv na cenu mnou držených akcií, trhy jsou nevyzpytatelné a souhrnnou psychologii účastníků trhů nelze prostě odhadnout. Není možné například dopředu rozpoznat a předurčit, jestli vyhlášené mimořádně skvělé hospodářské výsledky za uplynulé čtvrtletí nakonec nebudou znamenat kýžený dvouprocentní růst ceny akcie, protože je docela možné, že tento růst byl trhem očekáván a promítnut do ceny již před touto fundamentální zprávou, takové vyhlášení dobrých čísel pak může naopak způsobit úlevné potvrzení správného předpokladu analytiků, a to může v konečném důsledku vést dokonce k poklesu ceny. Každý si určitě takovou nevyzpytatelnou reakci trhů zcela jistě již prožil.

   Jak tedy naložit s historickými daty k vyhodnocení budoucího vývoje za současného přesvědčení, že nejsem vlastně schopen nic do budoucnosti přesně kvantifikovat? Jako opční obchodník mám komfortní možnost si dovolit nepřesně předpovídat směr budoucího vývoje a ještě na takových nepřesnostech vydělávat. To je velmi elegantní pozice oproti akciovým obchodníkům, kteří pro svůj výdělek nutně potřebují přízeň předpokládaného trendu, v opačném případě je čeká prodělek. Musí mě proto nutně zajímat, jaké bylo rozložení pohybů podkladů v minulosti a z této premisy pak extrapolovat své počínání do budoucnosti.

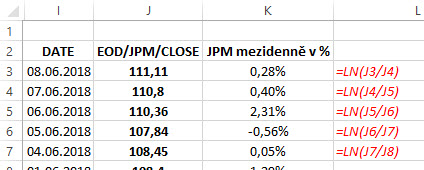
   Není nic složitého získat ucelenou řadu historických Close cen běžně obchodovaného akciového titulu. Pro svůj příklad použiji cenové údaje akcie JPM. Základní úvahou o budoucím pohybu akcií JPM tedy bude zjištění, jakým způsobem byly jednotlivé cenové pohyby rozloženy v minulosti a jakým způsobem by mohly být rozloženy v budoucnosti. K rozpoznání, zobrazení a interpretaci minulých pohybů mohu jednoduše vycházet z mezidenních pohybů cen této akcie. Musím mít ale na paměti, že vytvoření prostého rozdílu včerejší ceny a dnešní ceny nemá valnou vypovídací schopnost pro analýzy delších časových řad. Pokud stojí nyní akcie JPM zhruba 100 USD, potom absolutní mezidenní pohyb ve výši 3 USD znamená tříprocentní fluktuaci. Stejný třídolarový pohyb před pěti lety, kdy se cena akcie JPM pohybovala kolem 50 USD by ale znamenal 6% cenový pohyb. V analyzování těchto absolutních cenových mezidenních rozdílů by tak vznikala základní logická chyba. Je proto vhodné k zjištění takového mezidenního pohybu využít podíl těchto sousedních cen a získat tak historickou řadu mezidenních rozdílů na procentní bázi. Je pak jedno, jestli akcie stojí pětset dolarů nebo padesát, tříprocentní růst je pořád tříprocentní růst, i když v absolutních dolarových částkách jde o diametrálně jiné sumy. Současně se také musím vypořádat s problémem růstu a poklesu ceny a správném zachycení těchto rozdílů, pokud akcie s cenou 100 USD vystoupá za jeden den o tři procenta, její cena bude 103 USD, pokud ale vzápětí její cena poklesne o tři procenta, bude její konečná cena 99.91 USD, nikoliv původních 100 USD. Využiji tedy při výpočtu mezidenních rozdílů přirozeného logaritmu podílu Close cen pro sledovanou akcii, abych tento rozdíl eliminoval, pokud tedy dnes ukončila akcie JPM na hodnotě 111.11 USD a včera ukončila na hodnotě 110.80 USD, bude pak rozdíl vypočten jako ln(111.11/110.80) = +0.28%, což pak představuje hodnotu mezidenního růstu.

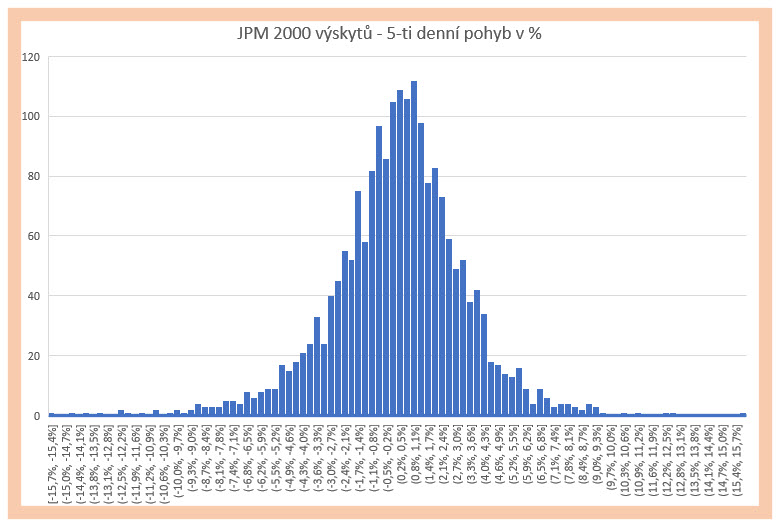
  Na obrázku níže je pro akcii JPM vyobrazeno rozložení jednodenních cenových pohybů vypočtených podle výše uvedené metody, přirozeného logaritmu podílu Close sousedních cen v jednotlivých obchodních dnech. 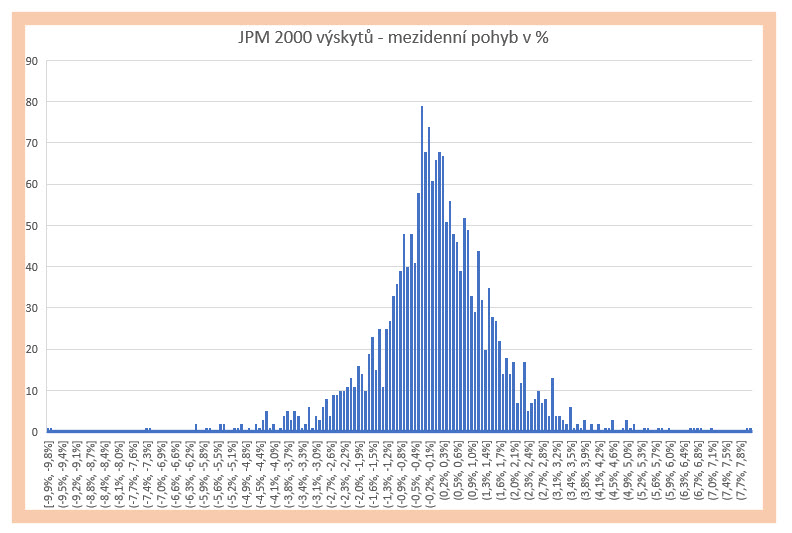        Distribuce cenových rozdílů je vytvořena z 2000 obchodních dnů, tedy zhruba za období posledních osmi let. Jednotlivé vypočtené cenové rozdíly jsou pak rozděleny do skupin podle pohybů lišících se o desetinu procenta. Je zcela jasně a zřetelně vidět, že největší výskyt je nahromaděn okolo průměrné hodnoty -0.50% do +0.50 %, vyšší cenové výkyvy ve sledovaných cenách jsou pak vzácnější vzhledem k těmto průměrným hodnotám, s tím, že čím je cenový výkyv vyšší, tím je jeho poloha vzdálenější ke středu vyobrazenému grafu. Mám tak možnost pozorovat klasické rozložení hodnot nazvané Normální Rozdělení, pospojované vrcholy úseček histogramu by pak vyformovaly velmi povedenou Gaussovu křivku.

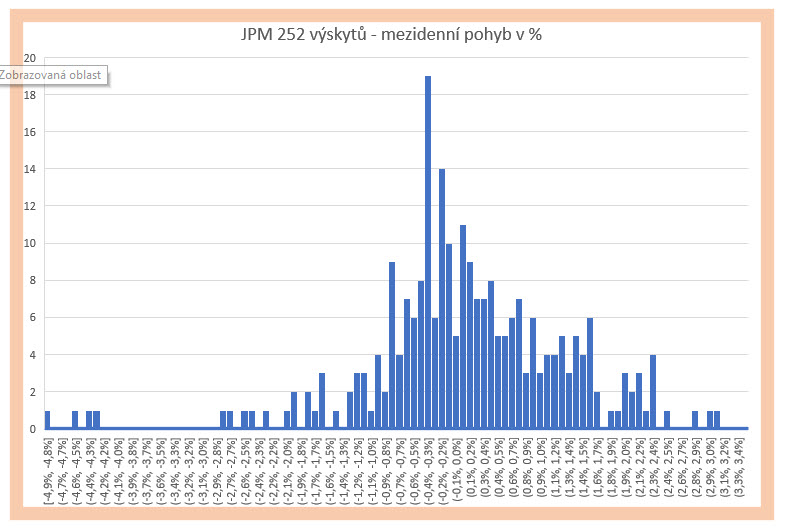
   Stejný obrázek bych mohl pozorovat, pokud bych počet výskytů (mezidenních rozdílů) zredukoval na období jednoho roku. Neměl bych tak „plynulé“ vyobrazení Normálního Rozdělení, ale všechny potřebné atributy by byly patrné i z takto malého vzorku vypočítaných dat.

   Pokud bych chtěl takto interpretovat například pohyb akcie v pětidenním časovém úseku a neomezovat se tak jen na mezidenní pohyby, mohl bych se stejným výpočetním postupem zjistit pětidenní cenové rozdíly, a tyto si potom interpretovat pomocí stejného grafu rozložení jednotlivých vypočítaných hodnot.

   Pozorovatelné efekty rozložení vypočítaných hodnot popisované výše jsou pak patrné i na datech rozdílů jiných než jen jednodenní cenový rozdíl.

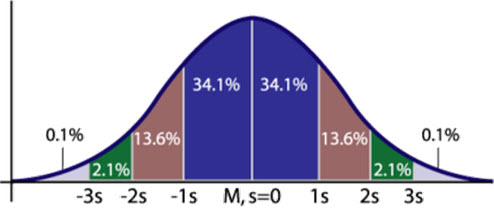
   Výchozím bodem mé úvahy o budoucích cenách akcií JPM by mohlo být zjištění, že historické rozložení cenových rozdílů má Normální Rozdělení, mohl bych se tedy pokusit o úvahu, jaké rozdělení budou mít ceny v budoucnosti. Je přirozené předpokládat, že pokud měly zjištěné historické hodnoty cenových rozdílů (mezidenních, pětidenních…) rozložení odpovídající Normálnímu Rozdělení, potom bude asi slušně pravděpodobné, že tuto distribuci cenových rozdílů budou mít také budoucí cenové rozdíly. Ponechám nyní stranou matematické důkazy tohoto tvrzení (toto bych chtěl ukázat v následujícím článku), pouze se spokojím s tvrzením, že pokud jsou cenové rozdíly zjištěné v minulosti „normálně rozložené“, budou takto rozložené i v budoucnosti. Pokud bych takové tvrzení vzal jako základ pohledu do budoucnosti, pak bych, z podstaty a vlastností Normálního Rozdělení, mohl předpokládat, že budoucí ceny se budou nacházet rozptýleny kolem střední hodnoty (průměrné ceny naměřeného pohybu) s pravděpodobností 68,20 % mezi touto střední hodnotou a hodnotou první standardní odchylky, s pravděpodobností 95,40 % mezi touto střední hodnotou a hodnotou druhé standardní odchylky a s pravděpodobností 99,80 % mezi touto střední hodnotou a hodnotou třetí standardní odchylky. Na obrázku níže je tento budoucí výskyt demonstrován na grafu, který se nachází v každé základní statistické učebnici.

   Toto je sice pěkná teoretická úvaha, je ale nutno ji převést do použitelného tvaru pro případné obchodování a také ji nějakým způsobem prakticky zobrazit a interpretovat. Pokud jsem tedy zjistil, že cenu opčního kontraktu tvoří Hodnota Strike, Délka života opčního kontraktu, vyplácená Dividenda, momentální Úroková míra, aktuální Cena podkladu a hodnota Implied Volatility, tak se mohu v tomto okamžiku zamyslet nad tím, jakým způsobem jsou určeny ceny jednotlivých opčních kontraktů, které vidím ve své opční platformě. Přesně nyní vím, jaká je že Hodnota Strike, Délka života opčního kontraktu, vyplácená Dividenda, momentální Úroková míra, aktuální Cena podkladu a s jakou Implied Volatilitou je v této ceně počítáno. Na níže uvedeném obrázku jsou tyto hodnoty vyznačeny

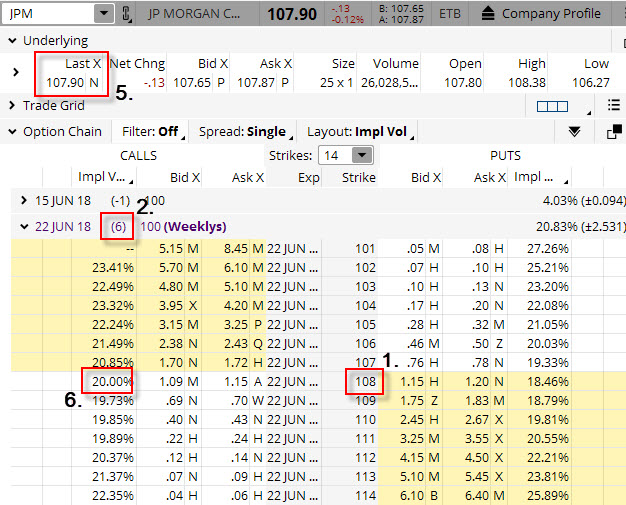
   Z obrázku (označeno jednotlivými čísly) vyplývá, že cena vyznačeného opčního kontraktu Long Call 108 pro akcii JPM by měla být tvořena:

• (1) Hodnota Strike je 108
• (2) Délka života opčního kontraktu je 6 dnů
• (3) Dividenda se v následujících šesti dnech nevyplácí (její cena nevstupuje do výpočtu ceny)
• (4) Úroková míra se v následujících šesti dnech nezmění a je pevně stanovena modelově na 1.75% p.a.
• (5) Cena podkladu je 107.90 USD
• (6) Implied Volatilita je stanovena na 20.00%

    Pokud bych chtěl předpovídat vývoj ceny opčního kontraktu do budoucnosti, můžu konstatovat, že v bodech (1) – (4) mohu přesně stanovit v jakémkoliv bodě v budoucnosti jeho přesné hodnoty. Například pro okamžik dva dny před expirací bude Hodnota strike pořád na hodnotě 108, Délka života opčního kontraktu bude na hodnotě 2 dnů, Dividenda a Úroková míra zůstanou nezměněny. U Ceny podkladu a Implied Volatility však nebudu vědět, jaké hodnoty bych měl použít. Protože neumím žádným způsobem předpovídat budoucí cenu a žádné smysluplné vodítko se mi k takové předpovědi nenabízí, nezůstává mi nic jiného, než vycházet z vyznačené hodnoty Implied Volatility a tento údaj využít k budoucí předpovědi – někdo jej totiž musel vytvořit a do opčního řetězce vyznačit.

    Za použití mého předpokladu, že ceny v budoucnosti budou mít Normální rozdělení, je Volatilita (pro potřeby výpočtu ceny opčního kontraktu) obecně definovaná jako cenový pohyb o velikosti první Standardní Odchylky v časovém horizontu jeden rok. Je vyjádřena v procentním tvaru jako procento z ceny podkladového aktiva. Jak si tedy mohu vysvětlit údaj 20% Implied Volatility u mého příkladu s akcií JPM. Nabízí se dvě jednoduché interpretace

   1/ Pokud akcie JPM dnes stojí 107.90 USD, tak za jeden rok by se s pravděpodobností 68.20% mohla pohybovat do 20% své hodnoty nad současnou cenou a do 20% své hodnoty pod současnou cenou. Cenové pásmo by pak bylo 86.32 USD – 129.48 USD

   2/ Pokud akcie JPM dnes stojí 107.90 USD, tak v roce, který bude následovat, by v 68,20% tohoto budoucího času mohla setrvávat v rozpětí 86.32 USD – 129.48 USD

   Obě vysvětlení pak využívají pravděpodobnosti pohybu daném definicí Normálního Rozdělení a z něj odvozených pravidel pro první Standardní odchylku. Protože je ale roční predikce prakticky využitelná jen málo a sloužila by například pro držení podkladového aktiva v horizontu přesně jeden rok, je nutné si takovou Implied Volatilitu umět vyložit pro jiné časové období. Využiji proto jednoduchý vzorec pro výpočet Volatility níže

   Ve vzorci je symbolem sigma označená hodnota roční Implied Volatility (tu kterou vidím v opčním řetězci) a pod odmocninou je hodnota času, pro kterou budu chtít Volatilitu vypočítat. Je pak patrné, že tímto výpočtem mohu provádět určitý stupeň „odannualizace“ na požadovaný jiný časový úsek popisovaný v článku Je opce levná nebo drahá? Protože Volatilita, vyobrazená v opčním řetězci představuje roční Implied Volatilitu, mohu například chtít zjistit, jak se bude pohybovat cena podkladu například na jednodenní bázi, k tomuto výpočtu bych pak použil  

   Výraz 20% je Implied Volatilita vysledovaná z opčního řetězce a pod odmocninou je hodnota 252 – průměrný počet obchodních dnů v roce. Vypočtenou jednodenní Implied Volatilitu pak použiji pro mou konkrétní akcii JPM, abych zjistil rozsah jednodenního pohybu

   Z výpočtu pak mohu odvodit, že v následujícím obchodním dnu se s pravděpodobností 68.20% (první Stadardní odchylka) bude cena akcie JPM pohybovat do +/-1.35 USD okolo své současné ceny.

   Mohlo by se zdát, že vypozorování jednodenního pohybu by nemuselo být praktické pro mé obchody, protože například budu chtít pozorovat pravděpodobnost pohybů v delším časovém horizontu než je jeden den, ale kratším než jeden rok. K takovému odhadu pak dobře poslouží právě vypočtená jednodenní hodnota Volatility z předchozího výpočtu. Pokud budu chtít zjistit pravděpodobnost měsíčního pohybu akcie JPM za předpokladu Normálního Rozdělení, potom taková jednoměsíční prognóza vychází z hodnoty jednodenní Volatility násobené druhou odmocninou hledaného časového úseku, v mém případě jsem pod odmocninu použil hodnotu 21 – počet obchodních dnů v kalendářním měsíci. Za denní Implied Volatilitu jsem použil dříve vypočtenou hodnotu jednodenní Volatility 1.26%

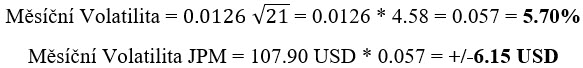
   Z výpočtu pak mohu odvodit, že v následujícím měsíci se s pravděpodobností 68.20% bude cena akcie JPM pohybovat do +/-6.15 USD okolo současné ceny. Stejný výpočet bych pak mohl provádět pro jakékoliv části roku a také jej, ve smyslu Normálního Rozdělení, interpretovat pro druhou Standardní odchylku. Potom bych například mohl usuzovat, že s pravděpodobností 95.40% (pravidlo pro druhou Standardní odchylku) se bude měsíční hodnota akcie JPM pohybovat v cenovém rozsahu +/- 12.30 USD (2*6.15 USD)…

   Do budoucnosti nevidím, takže se musím spokojit s přítomností a odvozovat z minulosti, nic jiného mi nezbývá. V článku Je opce levná nebo drahá? jsem popsal výpočet Historické Volatility na základě minulých pohybů cen podkladové akcie. Takový výpočet je velmi jednoduchý a rychlý, pokud mám dobrý zdroj dat, jsem schopen si takové výpočty provádět například ve svém Excelu. V článku jsem popsal výpočet hodnoty Historické Volatility na měsíční periodě, to znamená, že jsem vypočítal hodnotu Směrodatné odchylky za období 21 dnů, které představuje průměrný počet obchodních dnů v kalendářním měsíci. Vypočtenou hodnotu Směrodatné odchylky na této periodě jsem pak annualizoval násobením druhé odmocniny čísla 252 (průměrný počet obchodních dnů v roce), abych získal hodnotu Historické Volatility pro toto měsíční období. Mohu ale zvolit také jiné časové období a vypočítávat Historickou Volatilitu pro delší časové rámce, například pro 100 dnů, 150 dnů, 200 dnů a podobně, a to jednoduše tak, že budu zadávat výpočet Směrodatné odchylky právě na těchto odlišných obdobích. Mohu tak získat různé náhledy na Historickou Volatilitu podkladového aktiva, právě na základě počítané periody. Na obrázku níže jsou zobrazeny jednotlivé průběhy takových Historických Volatilit pro různé časové rámce pro akcii JPM pomocí obchodní platformy TWS, nemusím tedy nic počítat ve svém Excelu.  

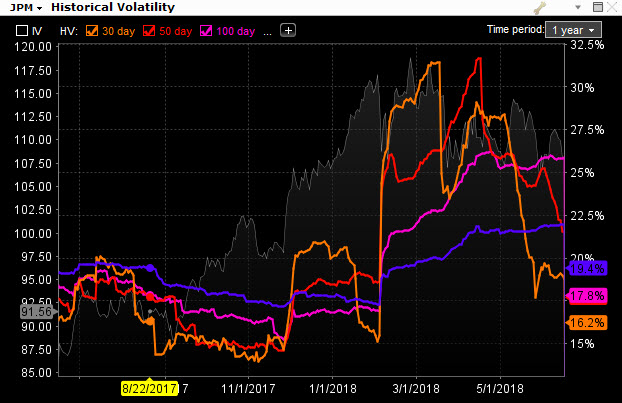
   Každá z křivek Historické Volatility s různou periodou počítané Standardní odchylky se svým průběhem mírně liší, základní tvary přímky zůstávají stejné, jenom se umocňuje dramatičnost průběhu v souvislosti se zkracováním této počítané periody. Hodnoty všech těchto průběhů Historické Volatility se ale liší od hodnoty Implied Volatility, vtělené do ceny opčních kontraktů. Někdy značně. Stanovení správné hodnoty Implied Volatility vstupující do ceny opcí pak může utvářet komplexní pohled na vývoj trhů podkladových aktiv právě z pohledu těch účastníků trhů, kteří se na tvorbě ceny podílejí a musí tak hodnotu Implied Volatility nějakým způsobem stanovit. Tyto jejich pohledy však nemusejí být nutně vždy správné. Kdyby totiž tito účastníci trhů měli vždy pravdu ve stanovování Implied Volatility, musela by se hodnota Historické Volatility a Implied Volatility ve zpětném pohledu do minulosti shodovat, to ale není prakticky možné, protože by pak panoval soulad mezi předpokládaným chováním ceny a skutečně pozorovaným chováním ceny podkladových aktiv, a to je již ze své podstaty neurčitosti trhů velmi nepravděpodobné. Pokud bych promítl hodnoty Implied Volatility do grafů Historických Volatilit uvedených v obrázku výše pro akcii JPM, mohl bych pozorovat, že se historický průběh křivky předpokládané Implied Volatility (bílá křivka níže v grafu) a křivek Historických Volatilit na různých periodách nějak významně neshoduje a „žije si svůj vlastní život“.   

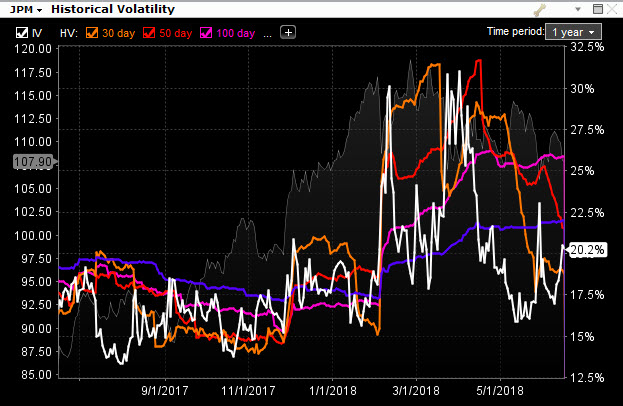
   Proč tomu tak je? Zejména proto, že výpočet Implied Volatility je postaven na jiných matematických základech než jednoduchý výpočet Historické Volatility (bez ohledu na možnost využívat různé historické periody pro Standardní odchylku). Stanovit Historickou Volatilitu je jednoduché, protože známe historické chování cen, jak se ale budou chovat ceny zkoumané akcie v budoucnosti je jiná písnička. Stanovení hodnoty Implied Volatility je tak sofistikovanou vědou, přesahující dimenze mého myšlení. Komplexnost matematických vzorců, armády analytických týmů a rozsah softwarového vybavení, to vše vstupuje do hry o stanovení správné hodnoty Implied Volatility nejenom pro správné stanovení ceny opčních kontraktů, ale také pro modely budoucího chování celých portfolií a jejich následnému správnému zajišťování právě v důsledků možných budoucích změn odhadované Implied Volatility a s tím související změny v pohybech podkladových aktiv. Netrápím se tak nyní způsobem, jakým tito účastníci trhů stanovují přesnou hodnotu Implied Volatility, protože to je pro mě nezjistitelná informace, mohu však do budoucna přemýšlet, jaký má vztah k Historické Volatilitě a co by to mohlo znamenat pro mé obchody.

   Na obrázku níže je možné pozorovat roční průběh například 30-ti denní Historické Volatility a Implied Volatility pro akcii AAPL

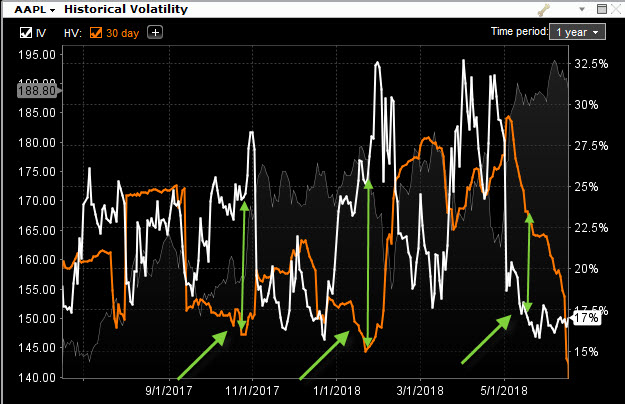
  Z obrázku je patrné, že Implied Volatilita a Historická Volatilita jakoby opravdu měly spolu pramálo společného. Je zřetelně vidět, že očekávané pohyby vyplývající z Implied Volatility se nakonec ve skutečném chování, vyjádřeném skutečnými cenovými pohyby reprezentovanými 30-ti denní Historickou Volatilitou, velmi diametrálně liší. Období znázorněné zelenými šipkami pak charakterizuje extrémy, kdy se tato očekávání rozcházela ve znatelnějším rozsahu. Pozoruhodností těchto grafů je pak v pozorování oddalování těchto křivek a jejich následné sbíhání, které by pak mohlo znamenat období, kdy Implied Volatilita narůstá, aby po dosažení nějakého svého maxima se opět vrátila na své původní úrovně a vytvářela tak na těchto grafech pomyslné „bubliny“ tvořené oběma křivkami volatilit. Velikost bublin je pak odrazem odlišného skutečného chování podkladového aktiva měřeného Historickou Volatilitou na 30-ti denní historické periodě od jeho chování očekávaného, reprezentovaného sofistikovaně vypočítanou Implied Volatilitou. Na dalším obrázku, pro ilustraci, stejné vyobrazení volatilit pro akcii JPM

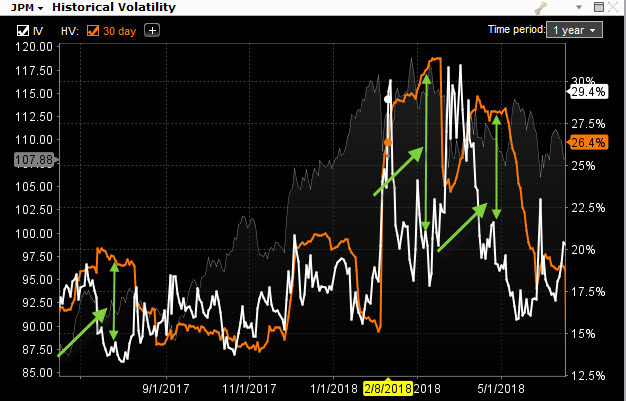
   Pokud bych tedy chtěl odvozovat své představy o budoucím pohybu sledovaného podkladu od Normálního Rozdělení a zejména vyznačené Implied Volatility, mohl bych podle předchozích řádků patrně stanovit budoucí pásmo, kde se bude cena podkladové akcie ve vypočítaném časovém horizontu pohybovat podle jednoduchého matematického výpočtu. Více než pravděpodobnost a stanovené cenové pásmo podle tohoto výpočtu bude ale zajímavé využít poznatku o Normálním Rozdělení, pravděpodobnosti a Standardní odchylce k analýze historických dat a na této analýze si udělat jednodušší představu, jakým způsobem by se mohla budoucí cena vyvíjet.

   Na obrázku níže je zobrazena cena akcií AAPL za poslední rok. AAPL je velmi známá technologická akcie a na její průběhu podle tohoto cenového grafu nevidím, z pohledu cenových pohybů, nic neobvyklého, obecný uptrend, s několika poklesy vystřídaných nárůsty.

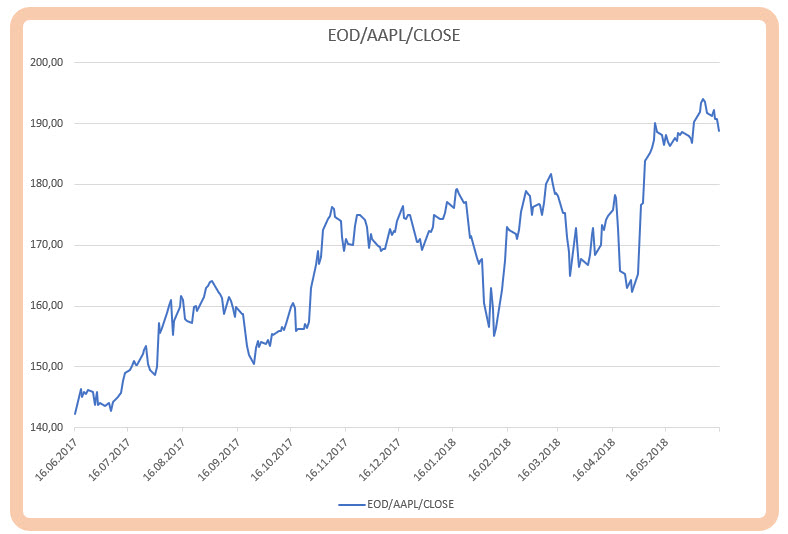
   AAPL je obrovská společnost, na kterou působí, mimo sektorové vlivy, mnoho globálních vlivů, takže ve svém průběhu lze pozorovat dobrou míru shody s akciovými indexy. Pokud bych si opatřil historická Close data za poslední rok zpět, mohl bych s nimi nějakým způsobem pracovat, například vypočítat průměrnou hodnotu mezidenního pohybu, maximální mezidenní pokles nebo maximální mezidenní nárůst a z těchto pohybů pak odvozovat parametry nejrůznějších možných obchodů. Protože se ale nyní zabývám problémem volatility, mohl bych  na tyto mezidenní pohyby nahlížet jinou optikou.

   Ve světle poznání, že by tyto mezidenní pohyby mohly mít Normální Rozdělení, bych mohl takovou skutečnost promítnout do těchto historických vypočítaných dat. K takovému zobrazení si pokusím převést historická data akcie AAPL do tvaru, kdy nebudu zobrazovat hodnoty mezidenních pohybů v procentním vyjádření, jak je to zobrazeno v histogramu pro akcii JPM výše v článku, ale pokusím se převést tyto data na mezidenní pohyby vyjádřené ve Standardní odchylce měřené na třicetidenní historické periodě (nejběžněji používané) a potom zobrazit podobný histogram, ale sestavený z těchto dat. Co tím získám? Jednoznačně přehled o míře  „uvěřitelnosti“ minulých pohybů z pohledu pravděpodobnosti jejich výskytů.

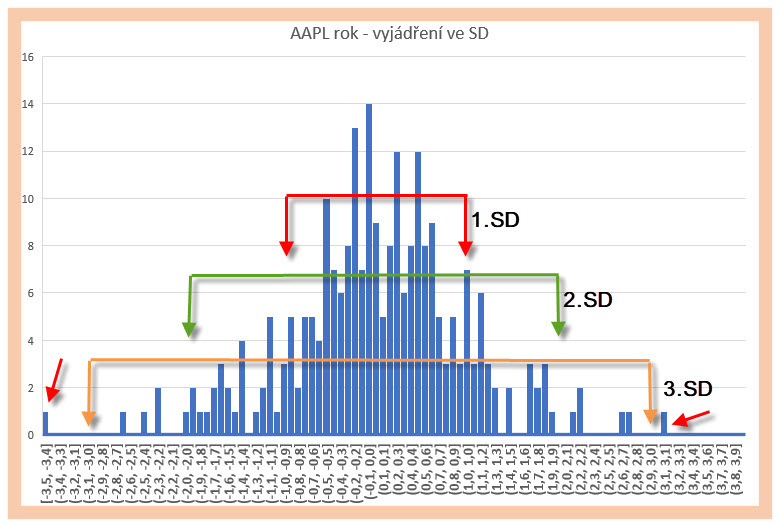
   Z histogramu je pak patrné, kolik, mezidenních pohybů se odehrálo s pravděpodobnostmi podle „pravidla tří sigma“, tedy podle Normálního Rozdělení. S pravděpodobností 68,20 % se nacházely hodnoty v intervalu označeném 1.SD (první standardní odchylka), s pravděpodobností 95,40 % se nacházely hodnoty v intervalu označeném 2.SD (druhá standardní odchylka) a s pravděpodobností 99.80 % se nacházely hodnoty v intervalu označeném 3.SD (třetí standardní odchylka). Pohledem na cenový graf akciového titulu nebo obecnou analýzou historických dat bych nemohl takové informace tak elegantně získat. Co je ale na takových datech pozoruhodné, přestože to z cenového grafu nevyplývá, je zjištění, že z takového histogramu také mohu vyčíst, že některé z pohybů leží mimo pásmo třetí Standardní odchylky na levém a pravém okraji grafu, které vyjadřují velmi neobvyklé cenové pohyby (malé červené šipky). Tyto pohyby mimo vyznačené pásmo třetí Standardní odchylky pak znamenají, že nastaly s pravděpodobností menší než 0.20% (za hranicí pravděpodobnosti 99.80%)!!! Takovou pravděpodobnost výskytu bych patrně ve svém obchodování vyhodnotil jako neopakovatelnou příležitost k opčnímu obchodu s určitou konstrukcí, například výpisem opčního kontraktu v bezpečné vzdálenosti od takto „vychýlené ceny“. Protože mi toto zobrazení v histogramu mnoho dalšího neříká, není toto zobrazení hodnot mezidenních rozdílů možná nejšťastnější. Použiji proto jiné zobrazení cenových pohybů převedených do Standardní odchylky, a to zobrazení těchto mezidenních na časové ose.

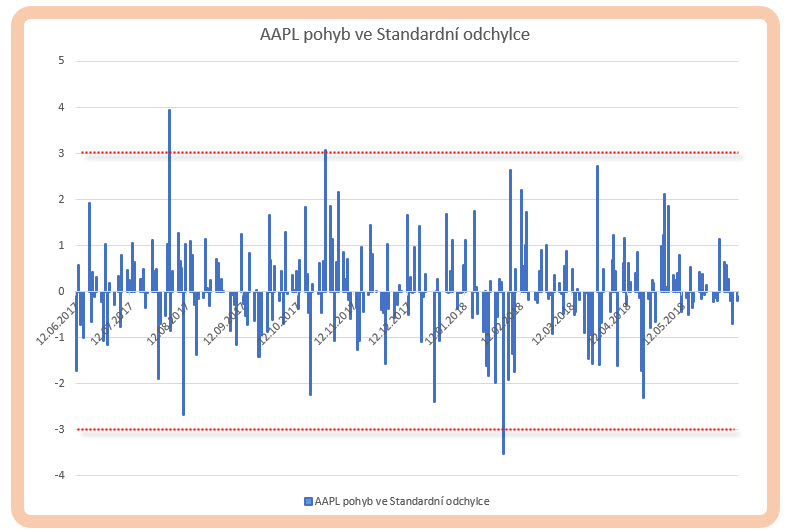
    Při pohledu na takto rozložený graf cenových pohybů podle Standardní odchylky musím konstatovat, že bych určitě nemohl z jednoduše analyzovaných dat jiným způsobem potvrdit, že mohly v průběhu minulého roku nastat prudké cenové pohyby na akcii AAPL s pravděpodobností menší než je 0.20%, tedy mimo třetí Standardní odchylku, dokonce byl nárůst v jednom z případů dokonce na úrovní čtvrté Standardní odchylky (toto se mi do histogramu výše ani nevešlo). Nemusím ale nutně pozorovat jen tyto vyhrocené extrémy, mohu vypozorovat dobrý počet cenových pohybů překračujících druhou Standardní odchylku, která bude znamenat, že v těchto případech se cena pohnula do oblasti, kde se neměla nacházet s pravděpodobností 95.40%, a to je již také velmi slušný „okraj společnosti“. K vyhodnocení jsem využil 30-ti denní periodu Standardní odchylky výpočtu minulých pohybů, mohu ale tutu periodu plasticky měnit a například ji prodlužovat, a dosáhnout jiného, možná robustnějšího, pohledu na pravděpodobnost cenových výletů mimo realitu všedního dne a vybírat tak jiné možné vstupní/výstupní body pro obchodování. Obecně řečeno „neuvěřitelnost“ těchto událostí by pak mohla být dobrým základem analýzy dat a zejména dobrým odrazovým můstkem pro vstupování do nejrůznějších obchodů podle individuálního nastavení. Nemusím připomínat, že sestavit jednoduchý Excel s možností načítání Close dat pro sledované tituly s vyhodnocením, kde se aktuální cena nachází ve smyslu této Standardní odchylky, je velmi jednoduchým úkonem. Takový velmi jednoduchý Excel s výše popisovaným výpočtem je ke stažení zde. Je do něj implementována (do buňky „DATE“) stahovací formule pro Close cenu AAPL s Quandl.com, takže pokud máte nainstalován doplněk Excelu pro data z tohoto zdroje, stačí jen povolit na pásu nástrojů z karty Quandl zatržítko u tlačítka „Formulas“ a po kliknutí na „Refresh Sheet“ se data zaktualizují pro daný den.

   K čemu to tedy vlastně je? Zdá se, že by nemuselo být špatné z hodnoty Implied Volatility odvozovat mnoho věcí užitečných pro můj trading. Protože nebudu pravděpodobně ve svých obchodech využívat hodnot mezidenních pohybů, ale mohu například chtít do nějakých pozic vstupovat v delších než těchto mezidenních intervalech a mohu přitom uvažovat o nějaké komplexnější strategii, budu asi schopen, po provedeném výpočtu chování této strategie v historii, zkoumat její budoucí potenciál na základě posouzení, jestli minulé výsledky měly Normální Rozdělení nebo nakolik se Normálnímu Rozdělení přibližují či dokonce zjištění, že Normální Rozdělení nemají. Testem normality bych pak měl být schopen takovou strategii odmítnout pro její nevyzpytatelnost nebo naopak vyčkávat na extrémnější pohyby v rámci předpokládané pravděpodobnosti a poté do svého testovaného obchodu vstoupit. Nebudu tak své očekávání například opírat o zjištěnou pravděpodobnost vzešlou z podílu počtu vítězný obchod/ztrátový obchod, ale o rozložení výsledků obchodů v provedené historické analýze z pohledu jejího rozdělení. Testováním normality budu například také rychleji dostávat odpověď na otázku, kde mohu čekat nahromadění určitých výsledků testovaných dat (pohybů, vítězných obchodů, ztrátových obchodů) s určitou pravděpodobností :c)