„… přestože se vžilo, že popis faktorů působících na tvorbu opční ceny jsme zvyklí označovat řeckými písmeny Delta, Gamma, Théta, Rho, Vega, tak musím podotknout, že Vega není písmenem řecké abecedy…“, v tomto smyslu většinou bývají uváděny články o „Vega“ zabývající se vlivem změny Implied Volatility na cenu opčního kontraktu, zřejmě proto, aby autor ukázal, že je kromě své zběhlosti ve znalostech opční problematiky také klasicky vzdělán a má tak samozřejmě v malíčku řeckou abecedu, kterou umí tam i zpět a to všechno je schopen dokázat samozřejmě i o půlnoci.

     Protože se cena opcí odvíjí od šesti vstupních hodnot, kterými jsou Ceny podkladu, Hodnota strike, Délka života opčního kontraktu, Implied Volatilita, Úroková míra a hodnota případně vyplácené Dividendy, tak mohu opět konstatovat, tak jako v minulých článcích, že Hodnota strike, Úroková míra a hodnota případně vyplácené Dividendy jsou „konstanty, které se za života opčního kontraktu nemění a na opční cenu tak bude mít vliv pouze změna hodnoty Ceny podkladu, Délky života opčního kontraktu a Implied Volatility. Změna hodnoty Ceny podkladu a jejich vlivu na cenu opčního kontraktu jsem se zabýval v článcích o Delta  a Gamma a vliv změny Délky života opčního kontraktu na cenu opcí jsem popisoval v článku o Théta. Zbývá tedy popsat, jak se do ceny opčního kontraktu promítá změna hodnoty Implied Volatility a bude tak hotov celý obrázek o principu tvorby opční ceny. O tom bude dnešní článek. 

   Takže, Vega není sice řecké písmeno, ale opravdu popisuje vztah mezi cenou opčního kontraktu a změnou Implied Volatility. Zjednodušeně nám ukazuje, o kolik se změní cena opčního kontraktu, když se hodnota Implied Volatility změní o 1%. Long Call na strike 150 má dnes cenu 320 USD a Implied Volatilita je na hodnotě 23%. Hodnota Vega je 22. Pokud hodnota Implied Volatility stoupne o 1% na hodnotu 24% a všechny ostatní cenotvorné prvky by zůstaly stejné, tak cena opce vlivem vzrůstu Implied Volatility způsobí, že nová cena opčního kontraktu Long Call 150 bude 320 USD + Vega (22) = 342 USD. Pokud Implied Volatilita poklesne o 1%, tak se cena opce o hodnotu Vega sníží a bude 320 USD – Vega (22) = 298 USD.

Matematika Vega

   Vzorec výpočtu hodnoty Vega, tak jak jej lze extrahovat z Black-Scholesova vzorce by vypadal jako na níže uvedeném obrázku a na rozdíl například od vzorce pro výpočet Théta nevypadá naštěstí tak děsivě komplikovaně.

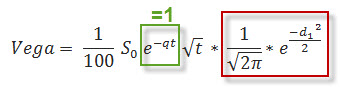
   Na obrázku jsem opět vyznačil oblasti, které povedou ke zjednodušení pochopení vzorce, zejména pro potřebu si takový výpočet převést do nějakého smysluplného tvaru a využít jej například ke svým vlastním výpočtům v jednoduchém Excelu.

  V zeleném obdélníku je exponenciální funkce, jejímž exponentem je součin hodnoty Dividendy a Délka života opce (-q*t). Protože jsem v článcích výpočtu ceny opcí a v článcích o Dividendách již uváděl, že hodnota Dividendy vstupuje do Black-Scholesova vzorce ve svém anualizovaném tvaru, můžeme se na hodnotu exponentu exponenciální funkce dívat, jako by byl téměř nulový a cokoliv téměř na nultou je téměř jedna, tato část vzorce tedy nemá na hodnotu Vega praktický vliv a můžeme ji z výpočtu vyloučit. 

 V červeném obdélníku jsem označil oblast, která představuje Distribuční funkci normálního rozdělení pro hodnotu –d1. Tuto hodnotu jsem již zjišťoval a ukazoval její matematický tvar v článku Cena opcí , tam jsem také využíval její hodnotu při určování ceny opce.  Její výpočet není složitý a Excel si s ní umí poradit a navíc je využívána i u jiných již ilustrovaných výpočtů, takže ji mám již ve svém ukázkovém Excelu již „předpočítanou“.

 Pokud bych tedy vynechal určitou nepodstatnou část vzorce z důvodu nepatrného vlivu (dividendová část) a celý vzorec počeštil, tak by vypadal jako na obrázku

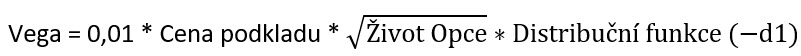
  Takovou vyobrazenou hodnotu pak mohu velmi jednoduše zadat do Excelu a vypočítat si hodnotu Vega pro různé vlastní potřeby. V ukázkovém excelovském sešitu, který je ke stažení zde, si pak po zadání hodnot do modře označených buněk můžu zjistit hodnotu Vega (při otevírání sešitu je zapotřebí odsouhlasit „povolit makra“). V Excelu je pak na kartě Vývojář možné zjistit VBA skript, pomocí kterého jsem vytvořil excelovskou funkci „=VegaOpce“, kterou můžu vyvolávat v kterékoliv buňce sešitu a po zadání argumentů podle návodu k funkci si takovou hodnotu také vypočítat. Celý skript pak můžete volně kopírovat a přenášet například do vlastních aplikací nebo sešitů.

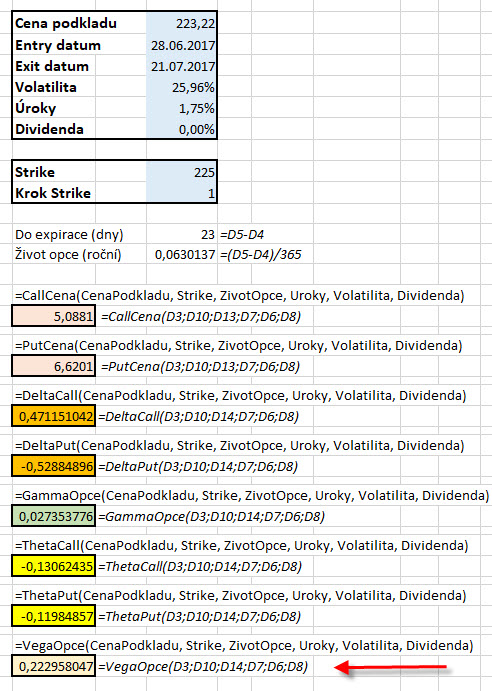
  Pokud bych shrnul principy výpočtů jednotlivých řeckých písmen a výpočtu cen opcí, které jsem zde ukazoval v několika předchozích článcích, mohl bych si pomocí takových vytvořených funkcí vyrábět celé jednotlivé opční řetězce i s vyobrazením hodnot jednotlivých řeckých písmen. Není to dnes nic složitého, abych získal zdarma z dostupných databází nebo zdrojů historické hodnoty cen podkladů, například akcií (Quandl.com…). Pokud bych byl ale schopen také získat historické hodnoty Implied Volatility těchto podkladů, tak bych byl schopen si vytvářet historické opční řetězce s cenami opcí a také s potřebnými hodnotami řeckých písmen pro jakýkoliv historický den. Není to žádná zvláštní věda, protože jsem ukazoval, jak si převést vzorce výpočtu ceny a řeckých písmen na jednotlivé funkce například v Excelu. V Excelu, který je výše ke stažení je takový „umělý“ opční řetězec pomocí takových funkcí vytvořen a je vyobrazen na níže uvedeném obrázku

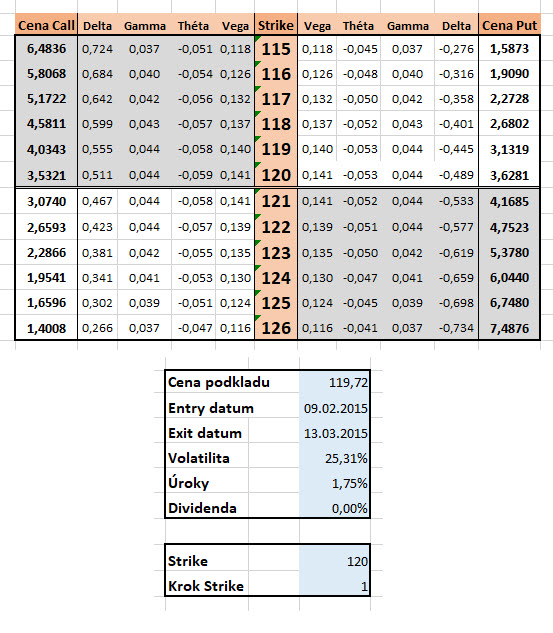
  Na obrázku je pak znázorněn opční řetězec akcie AAPL, jak by se takové opce obchodovaly i se svými „řeckými parametry“ před více než dvěma lety, například dne 9.2.2015, když v opčním řetězci jsou vyobrazeny a spočítány opce s expirací za měsíc dne 13.3.2015, při Implied Volatilitě 25.31%.

  O tom, že modelování pomocí jednoduchého Excelu není zcela mimo historickou realitu se můžete přesvědčit na obrázku z analytické platformy thinkorswim, která v jednom ze svých modulů umožňuje zjišťování historických cen opcí.

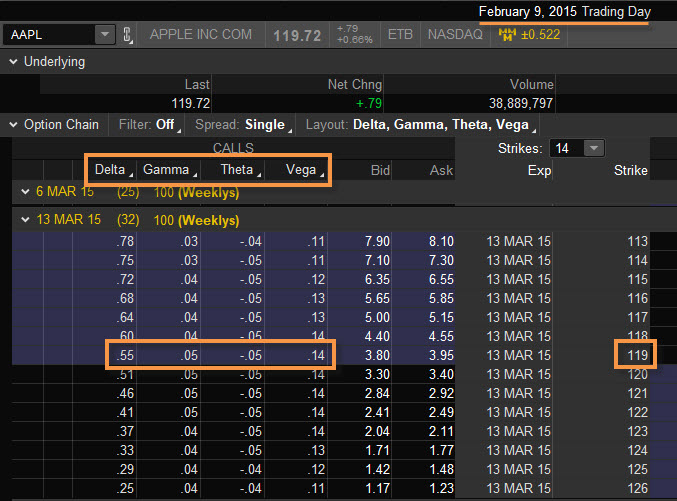
   Na obrázku je zobrazen úplně stejný stav opčních cen ze dne 9.2.2015 na opcích s expirací za měsíc při stejné volatilitě 25.31%, tak jako byly vstupní parametry použity do výpočtu pomocí Excelu. Ceny a „řecké parametry“ se liší velmi minimálně. Předpokládám, že ke generování historických cen používají sofistikovanější přístupy, než jsou funkce v mém Excelu, odvozené z Black-Scholesova modelu, ale podstata je myslím celkem plasticky zachycena.

Logika Vega

    Protože se jedná o poslední řecké písmeno, kterým se stojí za to zabývat, tak logiku velikosti hodnoty Vega srovnám s ostatními řeckými písmeny Gamma a Théta. Co mají všechna tato tři řecká písmena společného je skutečnost, že všechny tři řecká písmena Gamma, Théta i Vega mají své hodnoty na jednotlivých strike pro opce se stejnou expirací podobnou strikturu. Jejich nejvyšší hodnoty jsou u opcí, které mají ATM strike, tedy u opcí, jejichž strike je nejblíže k obchodované ceně podkladového aktiva. Všechny tři řecká písmena pak se svých hodnot sestupují, jak se jednotlivé strike vzdalují od ATM strike, a to v obou směrech. Všechny OTM opce a ITM opce mají hodnoty těchto tří řeckých písmen menší, než jsou jejich hodnoty na ATM strikes.

  Podstatným rozdílem je ale velikost těchto tří řeckých písmen, pokud se jedná o opce se stejnými strikes, ale v různých expiracích. Gamma a Théta mají své hodnoty na stejných strikes menší, čím více času opčnímu kontraktu zbývá do konce svého života. Pohledem do budoucnosti jsou jejich hodnoty stále menší. Vega je pravým opakem, opce na stejných strike, ale v jiných expiracích mají své hodnoty vyšší, čím více času opci zbývá do expirace. Co z toho vyplývá? Pokud máme otevřený opční kontrakt s velmi vzdálenou expirací, tak pohyb na podkladovém aktivu například o jeden dolar nebo úbytek času o jeden obchodní den nebude mít na cenu této vzdálené opce takový vliv, jako bude změna volatility. Čím vzdálenější bude expirace, tím bude tato disproporce vyšší. Na obrázku níže můžete takovou souvislost mezi vývoji jednotlivých řeckých písmen pozorovat

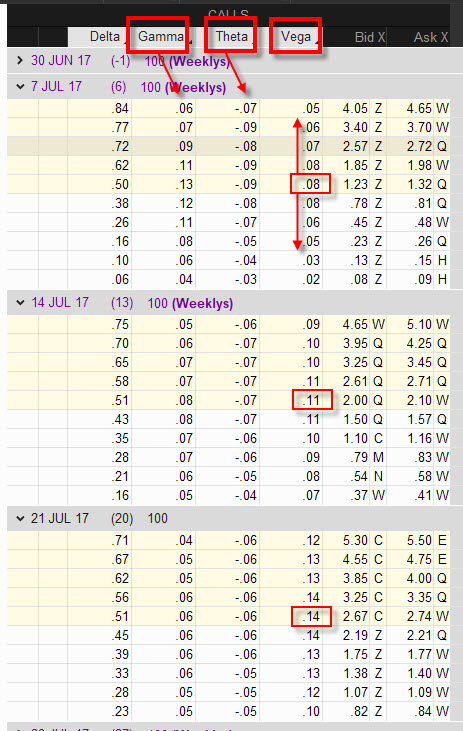
Vega Long opcí je kladná, Vega Short opcí je záporná

  Z pohledu znamének můžeme pozorovat stejnou konstelaci jako u Gamma. Má to samozřejmě svou logiku. Pokud bychom koupili opci Long a Implied Volatilita se zvýšila a všechny ostatní cenotvorné parametry zůstaly stejné, tak se také zvýší cena této Long opce, Long opce jsou tím dražší, čím je Volatilita vyšší, takže pokud jsme opci koupili levně a volatilita naroste, tak také naroste její cena. Mohli bychom pak takovou Long opci prodat za lepší cenu. Pokud ale opci vypíšeme a jsme Short opční kontrakt, tak při zvýšené Volatilitě a stejných ostatních cenotvorných parametrech se cena opce zvyšuje, to ale znamená, že pokud bychom chtěli takový opční kontrakt likvidovat, museli bychom na tuto likvidaci vynaložit více peněz, což by přineslo samozřejmě ztrátu.

   Součty hodnoty Vega opčních portfolií podle jednotlivých znamének (kladná Vega u Long opcí a záporná Vega u Short opcí) pak dává odpověď, do jaké míry je vystaveno celé portfolio působení kolísání Implied Volatility jednotlivých podkladů. Na níže uvedeném obrázku je podobná pozice jako v minulém článku, tedy ATM opce 3 x Long Call 144 a 3 x Long Put 144 (na stejném strike), celkově 3 x Long Straddle na akcii AAPL na strike 144 s expirací vzdálenou jeden měsíc.  

   Protože je opční pozice složena z Long opcí Call a Put, tak můžeme celkem slušně odhadnout, jaké budou hodnoty jednotlivých řeckých písmen pro celou pozici. Delta je na hodnotě +5, jsme tedy v Delta-Neutral pozici (delta je téměř nula). Gamma je kladná je na hodnotě +32, zjednodušeně to znamená, že pohyb podkladu jakýmkoliv směrem bude celé pozici jenom prospívat, znamená to, že celková Delta všech opcí by se při pohybu o jeden dolar zvýšila o hodnotu +32. Celková Théta je záporná a je na hodnotě -34, znamená to, že zítra, kdy opce ztratí ze svého života jeden den a mé 3 x Long Straddle se o jeden den přiblíží k expiraci, by byla cena mého 3 x Long Straddle menší o -34 USD, kdyby vše ostatní zůstalo konstantní. Vega celé pozice je na hodnotě +93. Znamená to, že pokud by se Implied Volatilita na trhu AAPL zvýší o 1%, tak celý 3 x Long Straddle nabyde na hodnotě o +93 USD, a to za předpokladu, že by se vše ostatní nezměnilo a naopak, pokud Implied Volatilita klesne o jeden dolar, utrpí má pozice ztrátu -93 USD jenom vlivem poklesu této volatility. To je dost peněz v sázce na tak malou pozici, jako je 3 x Long Straddle. Částka 93 USD tak představuje můj momentální risk celé opční pozice vůči změně Implied Volatility. Jak takové riziko eliminovat? Pokusit se o neutralizaci Vega pořízením/odebráním některých opčních pozic. Na níže uvedeném obrázku je podobná situace jak v minulém článku o Théta, kdy jsem hledal vhodný nástroj k mé pořízené pozici (byl to také 3 x ATM Long Straddle). Pořízení dalších opčních pozic pak v tomto článku mělo směřovat k neutralizaci Théta, abych celému opčnímu portfoliu odebral risk vyplývající z působení plynutí času na časovou složku držených opčních kontraktů. Stejně jsem tedy přistoupil k hledání vhodného instrumentu, abych se pokusil neutralizovat také hodnotu Vega. Na obrázku je vidět, jaké pozice byly pořízeny a jak se změnila hodnota jednotlivých řeckých písmen celého následného opčního portfolia.

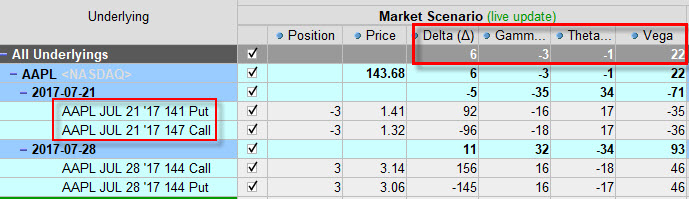
   K neutralizaci jsem si opět vybral pořízení 3 x Short Call opcí se strike ve vzdálenosti 3 body nad ATM strike a 3 x Short Put opcí ve vzdálenosti také 3 body pod ATM strike. Celý takový Short Strangle jsem pořídil s vypsanými opcemi v bližší expiraci. Co se stalo s riskem celého portfolia?

   Delta je na hodnotě +6, tedy se nezměnila a můžeme považovat takové portfolio opět za Delta-Neutrální. Gamma je na hodnotě -3, můžeme tak konstatovat, že portfolio je také Gamma-Neutrální. Ve shrnutí to pak znamená, že bezprostřední pohyb podkladu nebude mít na dolarovou hodnotu pozice valný vliv Théta je na hodnotě -1, plynutí času je téměř eliminováno, zítra by měla mít pozice svou hodnotu o jeden dolar vyšší, hodnota OTM Short opcí ze Short Strangle se bude rozpadat právě o ten jeden dolar rychleji než budou na ceně ztrácet vzdálenější Long opce z Long Straddle, potvrzuje to skutečnost, že jak se opce blíží ke své expiraci, je úbytek ceny způsobený plynutím času vyšší u opcí s bližší expirací, zatímco vzdálenější opce reagují na tento vliv vlažněji, portfolio můžeme také považovat za Théta-Neutrální. Hodnota Vega je na hodnotě +22, z původní hodnoty +93 klesla téměř na čtvrtinu. Snížili jsme tak risk vyplývající z pohybu Implied Volatility na přijatelnou částku. Proč se mi nepodařilo takovou „neutralizací“ srazit k nule také hodnotu Vega? Bylo by to skvělé, ale právě to vyplývá z popisovaného rozdílu velikosti hodnot řeckých písmen pro opce s nestejnou expirací. Zatímco u opcí s bližší expirací hodnota Gamma i Théta roste, tak hodnota Vega se snižuje, proto je výsledkem takové operace dodání potřebného množství Gamma a Théta, ale Vegy je přidáno méně než bych potřeboval.

  Co je ale na této „neutralizační transakci“ zajímavého je skutečnost, že pokud jsem se v minulém článku pokoušel o neutralizaci Théta přidáváním nějakých opčních pozic, tak jsem nevědomky neutralizoval také Gamma. Bylo to proto, že Gamma a Théta stejných opčních kontraktů (Long nebo Short), kterými chceme upravovat pozici do neutrality mají vždy opačná znaménka, proto neutralizace Théta směřuje k neutralizaci Gamma. Protože Vega a Théta stejných opčních kontraktů mají stejná znaménka, tak je také pochopitelné, že pokud takto neutralizuji Théta, tak jako v minulém článku, tak nevědomky také upravuji hodnotu Vega, protože se snažíme přidávat/ubírat opční pozice s opačnými znaménky, které se pak takovou neutralizaci snaží zajistit a tímto také opět neutralizuji Gamma. Neutralizace Vega tedy směřuje k neutralizaci Théta a také k neutralizaci Gamma. To ostatně také vyplynulo z našeho příkladu.

   Celá téměř neutrální pozice není nijak složitá co do pochopení celkového risku, protože si mohu představit její chování při jakémkoliv vývoji. Short Strangle na opcích v bližší expiraci je vzdálen tři body od strike opcí tvořících vzdálenější Long Straddle. 3 x Long Straddle jsem pořídil za náklad -620 USD, vypsáním Short Strangle jsem získal +273 USD. Celkový náklad na pozici je -347 USD. Mohly by pak nastat dva možné scénáře

 1/ Pokud by došlo k jakémukoliv pohybu v jakémkoli směru a došlo k proražení strike Short opcí bližšího Short Strangle -141/-147, tak při jejich expiraci bych obdržel vždy podkladové akcie provedení Assignment Short opce, která by byla „v penězích“. Těchto přiřazených akcií bych se ale jednoduše zbavil provedením Exercise Long opce se vzdálenější expirací (jedna z nich by totiž byla v takovém případě vždy „v penězích“), když výsledkem by bylo vždy získání +300 USD, jako dolarového vyjádření rozdílu strike těchto opcí Short a Long. Celkově by pak byly mé náklady jen -347 USD + 300 USD = -47 USD. Vždy by mi ale zůstala Long opce, která by nebyla Exercised a tato by mohla mít nějakou hodnotu, například právě těchto -47 USD, abych z pozice vyvázl bez ztráty.

2/ Pokud by strike některé opcí ze Short Strangle po nedostatečném pohybu nebyl proražen, pak by obě Short opce vypršely jako bezcenné. Mohl bych celý proces opakovat a vypsat další Short Strangle v bližší nebo stejné expiraci jako Long Straddle na strike nad Long Call a pod Long Put ve snaze získat další prémium…..

  Poznáním řeckých písmen a jejich aplikací na opční portfolio můžu získat větší nadhled nad složitějšími pozicemi. Mohu také rychle rozpoznat, co bude mému portfoliu prospívat a co mu může velmi uškodit. Mohu se také rozhodovat a prakticky konat, abych efektivně čelil expozici určitého risku vyplývajícího z každého jednotlivého cenotvorného prvku, který má mít vliv na profitabilitu celého komplexního opčního portfolia. Navzdory ukázkám v článcích o řeckých písmenech, jak taková rizika eliminovat musím nelibě konstatovat, že všechny vlivy na cenu opcí působí současně a hlavně se neustále mění a každý má svou vlastní dynamiku. Jak s těmito všemožnými vlivy bojovat musí pak být součástí obchodní výbavy a připravenosti každého jednotlivého obchodníka. Poznání řeckých písmen může být dobrou zbraní nebo doplňkem takové obchodníkovy výzbroje :c)