
Nevím, jestli Théta Kazí Libuši, protože nejsem vojvoda Krok, ale protože jsem opční obchodník, tak vím, jak Théta může zkazit i velmi dobrou opční pozici. V předcházejících článcích jsem již popisoval, jak se mění cena opčního kontraktu v souvislostí s pohybem podkladového aktiva a jak tuto závislost zachycujeme pomocí řeckého písmene Delta. V návaznosti na pozorování Delta opčního kontraktu jsem se pomocí Gamma pokusil popsat rychlost, s jakou se tato závislost změny ceny podkladu projevuje v cenách opcí. Protože se cena opčního kontraktu vypočítává například pomocí Black-Scholesova oceňovacího modelu, tak musím vyhodnotit, že kromě pohybu ceny podkladového aktiva má na cenu opčního kontraktu také vliv dalších pět faktorů kromě Ceny podkladu a těmito jsou – Hodnota strike, Délka života opčního kontraktu, Implied Volatilita, Úroková míra a hodnota případně vyplácené Dividendy. Protože jsem již zmínil, že Hodnota strike, Úroková míra a hodnota Dividendy jsou „zjistitelné konstanty“, tak zbývá k určení závislosti ceny opce na těchto šesti vstupních hodnotách pouze zachytit a popsat vliv Implied Volatility a Délky života opce (běžícího času) a mělo by být jasnější, jak celá skládanka vlivů změny těchto vstupních hodnot funguje.
Théta popisuje a měří, jaký má běžící čas vliv na cenu opčního kontraktu, o tom bude dnešní článek. V číselném vyjádření nám hodnota Théta sděluje, o kolik se změní cena opčního kontraktu za jeden den. Pokud má Long Call opce na strike 150 cenu 250 USD a hodnotu Théta -12, bude to jednoduše znamenat, že pokud by všechno zůstalo stejně (Cena akcie, Implied Volatilita, Hodnota úroků, Dividendový nárok a Strike), tak zítra bude hodnota této Long Call o 12 USD nižší a bude tak stát již jen 238 USD.
Matematika Théta
Vyhodnocením Black-Scholesova oceňovacího modelu by mělo být možné zjistit matematickou závislost běžícího času trvání opčního kontraktu na jeho cenu. Vzorce jsem samozřejmě nevytvořil sám, ale vzal je z odborné literatury. Nebudu pátrat, jak to bylo vypočteno, to je totiž mimo mé schopnosti, ale budu se snažit to alespoň mírně pochopit. Vzorec pro Théta pro Call opci a Put opci je na obrázku

Vzorce vypadají opravdu na první pohled hrozně. Na obrázku jsem u vzorce Théta Call opce vyznačil několik základních oblastí, které nám celý proces pochopení pro možné další zpracování může velmi zjednodušit.
V první červeném obdélníku je hodnota 1/T, kde T je počet dnů v kalendářním roce, tedy 365. Touto hodnotou se dělí nejvýznamnější část vzorce výpočtu. To je pro pochopení Théta pro tuto chvíli to nejpodstatnější zjištění. Vyplývá z něj, že Théta se mění každý kalendářní den., a toto je třeba opravdu registrovat, protože to není na první pohled patrné. Je to ale pochopitelné, čas běží pořád i když se s opcemi neobchoduje, tedy například o víkendech, čas nelze nijak zastavit nebo jej pošťouchnout rychleji vpřed. Pokud v pátek skončí obchodování na nějaké ceně s nějakou Delta a Gamma, tak tyto údaje nebudou v neděli odpoledne jiné, protože se o víkendu s podkladovým aktivem neobchoduje. Toto se však netýká Théta, protože čas plyne i o víkendu. V uvedeném příkladu s Long Call opcí na strike 150 a cenou podkladu v pátek na Close ve výši 250 USD a hodnotu Théta -12, tak budu muset konstatovat, že za sobotu a neděli hodnota opce ztratí 2 x -12 USD, tedy celých -24 USD. Pokud by akcie otevřela v pondělí na Open a pokud by všechno zůstalo stejně (Cena akcie, Implied Volatilita, Hodnota úroků, Dividendový nárok a Strike), tak by má Long Call 150 stála již jen 250 USD – 24 USD = 226 USD.
V zeleném kroužku umístěném v čitateli zlomku je exponenciální funkce, jejímž exponentem je součin hodnoty Dividendy a Délka života opce (-q*t). Protože jsem v článcích výpočtu ceny opcí a v článcích o Dividendách uváděl, že hodnota Dividendy vstupuje do Black-Scholesova vzorce ve svém anualizovaném tvaru, můžeme se na hodnotu exponentu exponenciální funkce dívat, jako by byl téměř nulový a cokoliv téměř na nultou je téměř jedna, tato část zlomku tedy nemá na hodnotu Théta praktický vliv a můžeme ji z výpočtu vyloučit.
V dalším červeném obdélníku jsem označil oblast, která představuje Distribuční funkci normálního rozdělení pro hodnotu d1. Tuto hodnotu jsem již zjišťoval a ukazoval její matematický tvar v článku Cena opcí, tam jsem také využíval její hodnotu při určování ceny opce. Její výpočet není složitý a Excel si s ní umí poradit a navíc je využívána i u jiných již ilustrovaných výpočtů, takže ji mám již ve svém ukázkovém Excelu již „předpočítanou“.
Pro oblast označenou zelenou elipsou platí stejná interpretace jako pro oblast označenou zeleným kroužkem, do hodnoty Théta vstupují anualizované Dividendy, takže zanedbatelná hodnota, kterou nemusíme do svého výpočtu zahrnovat.
Pokud bych tedy celý vzorec takto „osekal“ a počeštil, tak si mohu jeho matematický tvar v češtině vyobrazit tak, jak je vidět na níže uvedeném obrázku.

Podle takového vzorce by pak neměl být problém si Theta vypočítat například v Excelu, protože obsahuje pouze jednoduché matematické operace se vstupními hodnotami a využívá funkce, které již byly použity v předchozích výpočtech ceny opcí nebo řeckých písmen. V takovém excelovském sešitu jsem vytvořil dvě funkce pro výpočet Théta Call a Théta Put opcí a je možné je spouštět kdekoliv tomto sešitu po zadání funkce „=ThetaCall“ nebo „=ThetaPut“ se zadáním argumentů podle níže uvedeného obrázku.
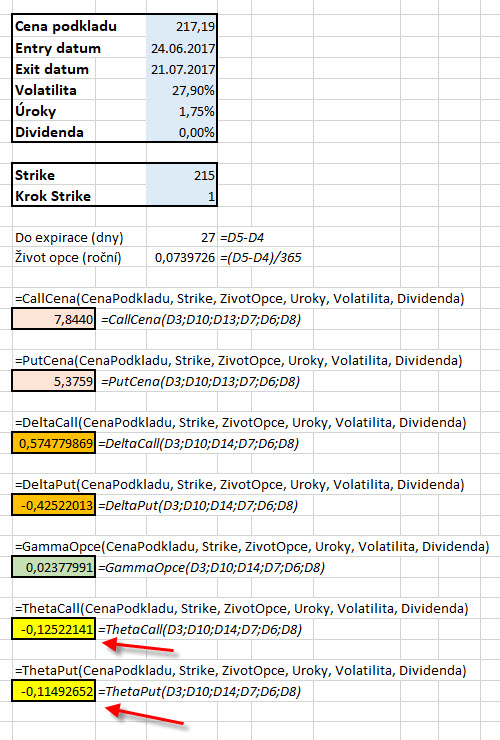
Tento jednoduchý sešit v Excelu je ke stážení zde a také si můžete na záložce Vývojář zobrazit ve VBA jednoduchý kód vzorce k výpočtu, tento si můžete volně kopírovat například do vlastních tabulek. Při otevírání staženého sešitu musíte na výzvu programu „povolit makra“.
Možná to celé vypadá zbytečné, takto pitvat a zabývat se složitými matemetickými vzorci, když v každé slušné obchodní platformě jsou již řecká písmena zobrazena. Vždy, když jsem otevřel nějakou publikaci o opcích, tak jsem narážel na podobné složité vzorce a kladl jsem si otázku, jestli to není zbytečné to do těchto publikací dávat, kdo to vlastně čte nebo rozumí tomu vůbec někdo? Při bedlivějším pohledu na takové chuchvalce znaků a výrazů a jejich převod na české výrazy jsem pak ale zjišťoval, že to zase tak složité není, že se to tak vlastně jenom složitě tváří. Proto se snažím takové zjednodušování ukázat ve svých článcích, snad to nevadí…
Logika Théta
Hodnota Théta jednotlivých opcí na jednotlivých strikes mají velmi podobnou logiku, jako má hodnota Gamma z předchozího článku, což bude mít své důsledky popisované dále. Protože nejvíce prémia je obsaženo v ceně opcí na ATM strike, tedy na strikes, které jsou nejblíže obchodované ceně podkladového aktiva, bude také hodnota Théta na těchto ATM strikes nejvyšší. Na strike, které jsou vzdálenější od těchto ATM strike hodnota Théta klesá, a to v obou směrech, tedy klesá u opcí se strike, které jsou více „mimo peníze“ a také stejně klesá, jak se opce více „ponořují do peněz“, tedy čím více OTM nebo ITM, tím je hodnota Théta nižší.
Stejně to platí také pro jednotlivé expirace. U opcí, které mají stejný strike, ale jinou expirací platí, že čím více má opce svou expiraci vzdálenější, tím je hodnota Théta nižší. Časová hodnota – prémium – u velmi vzdálených opcí tak na plynutí času nereaguje tak citlivě, jako cena opcí s bližšími expiracemi. Opce s nejbližší expirací pak mají hodnotu Théta nejvyšší, zjednodušeně řečeno, jak se krátí opci čas jejího života, tím zběsileji má Théta schopnost působit na snižování a rozpad její ceny. Na obrázku můžete vidět jednotlivé hodnoty Théta pro jednotlivé expirace a jednotlivé strike.
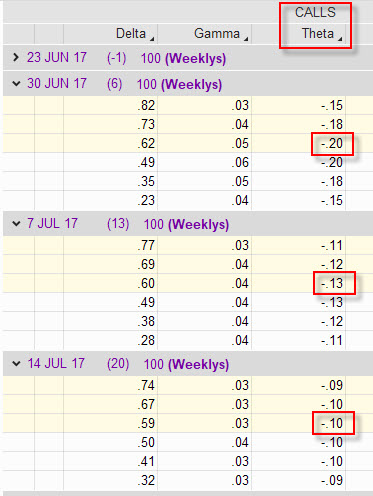
Základní logika pro sledování celkové expozice mého opčního portfolia vůči plynoucímu času pak bude vycházet z celkové hodnoty Théta mých opčních pozic. K takovému přístupu pak budu muset opatřit hodnotu Théta patřičným matematickým znaménkem.
Théta Long opcí je záporná, Théta Short opcí je kladná
Pokud budu držitel Long Call opce nebo Long Put opce, bude čas pracovat v můj neprospěch, pokud se nebudou patřičně pohybovat ostatní cenotvorné prvky hodnoty mých Long opcí, tedy nebude dostatečný pohyb na podkladovém aktivu nebo bude klesat nebo stagnovat Implied Volatilita. Pokud by tyto prvky byl neměnné, tak o hodnotu Théta bude cena opce každodenně neúprosně nižší. O hodnotu Théta (zápornou) by se tak každodenně zvýšila má ztráta na takovém Long opčním kontraktu, o tuto hodnotu Théta méně bych byl schopen na trhu takovou opci prodat a ztrátově vystoupit z pozice.
Vypisovatel Short Call nebo Short Put opcí to mají s hodnotou Théta přesně naopak. Čas pracuje pro vypisovatele. Pokud ostatní cenotvorné prvky jako je Pohyb podkladu a Implied Volatilita budou nevýrazné, bude hodnota Théta každý den ubírat na ceně vypsaných opcí, a to je přesně to, co si vypisovatel přeje. Pokud by se podklad nepohyboval a Implied Volatilita byla neměnná nebo se snižovala, tak o hodnotu Théta (kladnou) by Short opce pro vypisovatele každý den ztratila na své hodnotě, což by prezentovalo hodnotu zisku na tomto opčním kontraktu, o tuto hodnotu Théta méně bych byl schopen na trhu takovou opci koupit zpět a vystoupit ziskově z pozice. O kladnou hodnotu Théta tak roste můj profit.
U složitějších opčních pozic pak mohu pomocí celkové hodnoty Théta zjišťovat, nakolik je takové složitější portfolio vystaveno riziku plynoucího z běhu času mých držených opčních pozic. Na níže uvedeném obrázku je vidět jednoduchá Delta-Neutral opční pozice 3 x ATM Long Straddle na akcii AAPL s expirací za jeden měsíc. Obě Long opce Call i Put jsou na strike 146, Delta-Neutralitu jsem vytvořil pořízením 23 Short akcií AAPL.
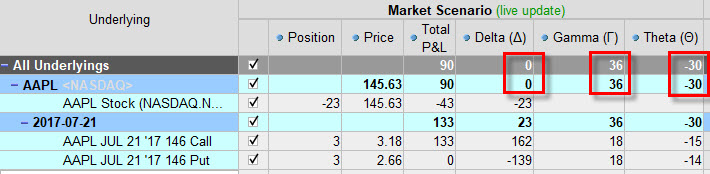
Tato Delta-Neutral opční pozice, tak jak je vidět na obrázku má Delta na hodnotě 0, její celková Gamma je 36 a celková hodnota Théta je -30. Co to znamená? Kladná Gamma znamená, že opční pozici bude velmi svědčit pohyb v jakémkoliv směru, protože je kladná. Čím větší pohyb tím lépe, to vyplývá z popisovaného stavu Gamma v minulém článku. Hodnota Théta je záporná a je na hodnotě -30. Neznamená to nic jiného, že pokud se akcie AAPL nepohne ani o cent a nevzroste Implied Volatilita, tak zítra bude hodnota mých 3 x Long Straddle o -30 USD nižší, a to by bylo nepříjemné.
Jak tedy čelit ztrátě hodnoty takového portfolia působením této záporné Théta? Provedením její neutralizace. Protože jsem popisoval, že hodnota Théta je vyšší u opcí s bližší expiraci, ale že je nižší na strikes, které jsou vzdálenější od ATM strikes, budu k neutralizaci hledat pořízení takového nástroje, který mi takovou neutralizaci zajistí. Na obrázku jsou vidět další pořízené pozice a nové hodnoty Théta.
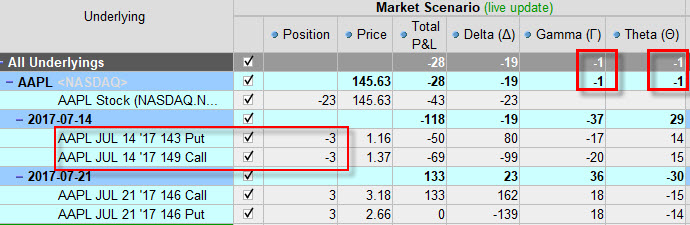
Zapomněl jsem uvést samozřejmou věc, kterou je, že pořízení podkladového aktiva nemá na hodnotu Théta žádný vliv. Podkladové akcie žádnou časovou složku ve své ceně obsaženou nemají, musím tedy hledat pro neutralizaci Théta pouze opční pozice, tyto mohu do svého portfolia přidávat nebo je ze svého portfolia odebírat. Pro úpravu pozice 3 x Long Straddle s negativní Théta jsem tak hledal adekvátní opční pozice, kterými bych dodal do portfolia tolik Théta, aby byla celkově téměř nula. Vybral jsem si 3x Short Call na vyšším strike s bližší expirací a 3x Short Put na nižším strike s bližší expirací. Výběr bližší expirace jsem provedl proto, že Théta opcí v bližších expiracích je vyšší než ve vzdálenější, kde již mám původní Long opce, opce se vzdálenějším strike od ATM jsem volil proto, že mají Théta nižší než opce s ATM strike, takže by tato obchodní operace mohla zajistit při stejném množství nových kontraktů dodání stejného množství Théta. Prodal jsem vlastně 3 x Short Strangle na bližších strike. Pokud se podívám na nové hodnoty Gamma a Théta tak zjišťuji velmi kuriózní věc. Celková hodnota Gamma je -1 a celková hodnota Théta je také -1.
Neutralizace Théta směřuje k Neutralizaci Gamma
Z minulého článku o Gamma vyplynulo, že hodnoty Gamma pro Long opce jsou kladné a pro Short opce jsou záporné. U hodnoty Théta je tomu přesně naopak. Pokud tedy neutralizuji hodnotu Théta, tak také směřuji k neutralizaci hodnoty Gamma. Co to celé znamená? Odejmul jsem pozici risk vyplývající s pohybu podkladu a také z působení běhu času. Protože je má pozice jednoduše čitelná, tak vím, že mám OTM Short Strangle na bližším strike a ATM Long Straddle na vzdálenějším strike. Pokud se cena pohne některým směrem, tak sice Short opční pozice nového Short Strangle půjdou proti mně, ale vzdálenější Long opce původního Long Straddle budou pracovat v můj prospěch, tento prospěch z Long Straddle bude díky svému strike vždy vyšší než ztráta ze Short Strangle. Pokud bych si představil pohyb celé pozice v čase a sledoval, s jakou dynamikou se bude vyvíjet Théta mé pozice, tak bych mohl zjistit, že pokud by se podklad velmi nepohyboval a zůstával by na stejné úrovni, tak by se Théta zvyšovala směrem k expiraci první části pozice (Short Strangle). Po expiraci tohoto Short Strangle bude opět záporná, protože mi zůstanou pouze vzdálenější Long opce původního Long Straddle. Mohu pak provést další podobnou neutralizaci pořízením Short Strangle nad/pod mými Long opcemi. Tím dodám do pozice potřebnou dávku Théta, ale hlavně další prémium, které by mělo financovat původní náklady na pořízení Long Straddle. Pokud by tyto „neutralizační“ Short opce byly ve stejné expiraci jako jsou opce Long Straddle, vytvořil bych tak na každé straně Call i Put vlastně Vertikální Spready (Bull Call Spread a Bear Put Spread) a pokud by součet hodnoty prémií získaných všemi minulými i současnými Short opcemi byl vyšší než jsou pořizovací náklady na původní Long Straddle, byl bych jistý vítěz…
Jediný risk, který mi zůstal, a který jsem pozici neodejmul, je risk vyplývající z Implied Volatility, jako poslednímu cenotvornému prvku, který jsem zatím nezafixoval (o něm někdy příště).
Přidáváním (ubíráním) opčních pozic Long nebo Short na obou stranách Long i Put pak mohu nejen podle celkových součtů hodnot řeckých písmen Delta a Gamma, ale také Théta, snižovat expozici portfolia vlivům tržního prostředí, kterými jsou v případě opčního obchodování pohyb podkladu současně s během času :c)
Sleduj facebook, napiš e-mail nebo tweet
Zrovna jsme dělali pokus na historických datech SPY s thetou a vychází to, že theta je nejmenší na striku 3 USD pod ATM. Proč, to vlastně nevím. Počítáme si jí ve skriptu, nemáme to z platforem.
Zdravím, tomu nerozumím, théta se snižuje, čím více je opce „v penězích“ nebo „dále od peněz“, nejvyšší je na ATM strike, můžete rozvést myšlenku Vašeho pokusu…. :c)
Nojo, to je pravda. Myšlenka pokusu byla prostě si spočítat na kterém striku je nejmenší Theta, jestli se to někdy neliší. Koukám se na náš kód kterým to počítáme a někde tam asi bude chyba ve vstupních parametrech, které pouštíme do funkce RQuantLib, kterou v tomto pokusu používáme na počítání Thety. Takže díky za ťuknutí do myšlenkové kuličky, už se rozkutálela a snad se dokutálí do důlku 🙂
Zdravím, Sosnoff a Battista na tastytrade uvádzali grafy rozpadu časovej hodnoty, kde exponeciálny priebeh rozpadu časovej hodnoty platí pre ATM striky, presne ako píšete v článku. Pre OTM a ITM boli v grafoch takmer lineárne priebehy priebehy, čo mi nesedí celkom s tým, čo sa všade uvádza. V tomto prípade by mala byť théta približne rovnaká počas trvania opcie (ak by sa nezmenili ostatné premenné a podkladovvé aktívum by nerástlo ani neklesalo). Z opčného reťazca v článku je zrejmé, že pre OTM a ITM opcie je pre vzdialenejšie expirácie théta menšia, ale pokles nie je taký výrazný ako pre ATM opcie. Každopádne nie je rovnaká ako by bola pri lineárnom priebehu rozpadu časovej hodnoty. Dalo by sa vniesť trochu svetla aj pre thétu pre OTM a ITM striky? Ďakujem.
Ahoj Miro,
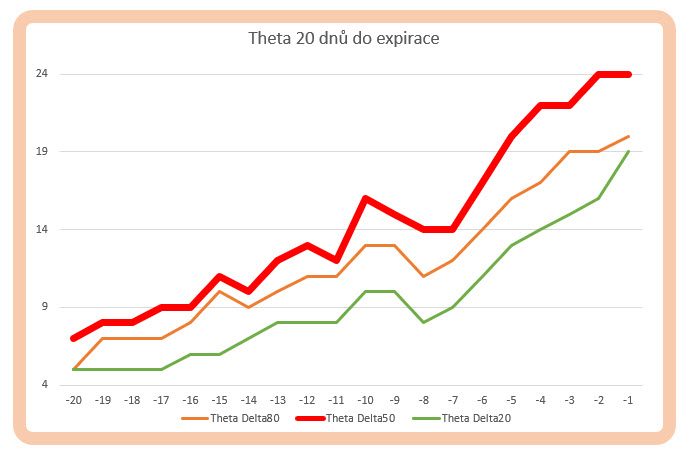
ze vzorce výpočtu hodnoty Theta jednoznačně vyplývá, že její výše graduje s běžícím časem do expirace. Ve jmenovateli výpočtu je v první velké závorce ve jmenovateli prvního zlomku hodnota 2*odmocnina (T), kde T je doba života opčního kontaktu. Pokud budu výpočet provádět pro deset dnů do expirace, tak T=10, výsledný výpočet jmenovatele zlomku je pak zhruba šest, potom by zlomek nabyl hodnoty modelově 1/6. Pokud budu výpočet provádět pro pět dnů do expirace, tak T=5, výsledný výpočet jmenovatele zlomku je zhruba čtyři, potom by zlomek nabyl hodnoty modelově 1/4. Pokud budu něco násobit *1/6 – dostanu vždy méně než bych něco násobil *1/4. Proto bude hodnota Théta narůstat s blížící se expirací, navíc je vzorec funkcí strike (X), takže platí pro všechny strike. V čitateli prvního zlomku je navíc aktuální hodnota podkladového aktiva a celý vzorec je zamotán do Distribuční funkce normálního rozdělení, je zařízeno, že strike který je vzdálen „od peněz“ v obou směrech (ITM i OTM) má Théta menší než na strikes, které jsou ATM. Selským rozumem pak můžu říct, že když něčeho zaručeně ubývá, tak nejvíce ubývá tomu, kdo toho má nejvíc – to jsou opce se strike s největším prémiem, které jsou na ATM opcích a pomaleji ubývá tam, kde je toho méně (OTM a ITM strike s malými prémii). Na obrázku níže jsou vyneseny křivky hodnoty Théta u akcie AAPL dvacet dnů do expirace tak, jak se Théta vyvíjí až k této expiraci.
Protože se cena podkladu neustále mění, jsou zachyceny hodnoty Theta u strike s Delta 50 (ATM opce), Delta 80 (ITM) opce a Delta 20 (OTM´) opce, je tak potlačen vliv pohybu podkladu. Théta se zvyšuje u všech pozorovaných strike směrem k expiraci, nejvyšší nárůst pak logicky má červená křivka pro ATM strike.
Možná, kdybych se zabýval obdobími rok do expirace, budou jednotlivé křivky působit jako horizontály (nebo možná jakési rovnoběžky) ale konec života by byl takový jako na obrázku, kdy tyto změny gradují. Lepší vysvětlení mě nenapadá, ahoj, Jirka
Ďakujem pekne za objasnenie, aj za námahu s grafmi.
Miro
Zdravím. Díky za zajímavý článek, ale dovolím si upozornit na některé nepřesnosti. V článku se uvádí, že nejvyšší hodnota thety je u opcí ATM. Ve skutečnosti je tam ale hodnota thety nejnižší. Dále se v článku uvádí, že long call a put opce mají zápornou thétu. To sice platí ve většině případů, ale ne vždy. Například evropská ITM put opce bude mít kladnou thetu (existují i některé speciální případy call opcí s kladnou thetou – např. evropská ITM na měnu s velmi vysokou úrokovou mírou).
David
Ahoj Davide,
popisuji v článcích opční kontrakty na equties, futures – nejběžnější podklady, tam je Theta nejvyšší u ATM strike. Na obrázku níže je opční řetězec SPX, patrně nejznámější opce evropského typu s vyznačenými Théta.
Průběh Theta je obdobný, měnovým opcím se zde prozatím nevěnuji vůbec, protože obchody s měnami neprovozuji. Mám ale návrh, pokud by jsi chtěl o těchto opcích něco napsat nebo máš s nimi nějaké obchodní zkušenosti, nebyl by problém to tady zveřejnit, na měnové opce jsem dostal hodně dotazů. Díky za komentář a měj, Jirka :c)
Jasně, ale tím, že jsou to záporný hodnoty, tak u ATM je theta vlastně nejnižší, ale to je spíš taková drobnost :-). Jinak měnovým opcím se taky nějak moc nevěnuji. Spíš jsem chtěl upozornit, že se takové případy mohou vyskytnout.
David
Ahoj Jirko,
je jasné, že čas běží i přes víkend a to by mělo ovlivnit cenu opce. Na druhou stranu o víkendu jsou trhy zavřené a není možné s opci nijak disponovat. O událostech, které se stanou před víkend můžeme uvažovat jakoby se stali přes jednu noc v týdnu. Počet obchodních a neobchodních dní je předem známý. Mne tedy stále vrtá hlavou, proč není cena opcí snižována o thétu pouze na základě obchodních dní. Myšleno: v případě že na začátku obchodního dne koupím opci na 15 dní, která expiruje v pátek, tak se mi každý den poníží cena opcí o théta/11 namísto théta/15.
Doufám, že jsem se jasně vyjádřil.
Petr
Ahoj Petře,
takto je čas do ceny opce promítnutý na základě Black-Sholesova oceňovacího modelu. Pokud bych vzal v úvahu další proměnné, které vstupují do ceny opce – pohyb podkladu a Implied Volatilita, tak tyto proměnné se mění (pohybují) pouze ve chvílích, kdy se s podkladem obchoduje a v těchto obchodních seancích také mění své hodnoty, i když nastane nějaká „cenotvorná“ událost například o víkendu, tak podklad vykoná pohyb a IV se změní až při pondělním opčním Open. Čas ale běží pořád, víkendy/nevíkendy, nemůže ho ovlivnit poptávka ani nabídka a dá se dobře a s jistotou měřit. Podotýkám, že já jsem to takto nezařídil, takže nezbývá než to takto brát, nic s tím nenaděláme….:c)