„Cena akcie AAPL je nyní 100 USD“ je tvrzení, které jsem pronesl v jakémsi podivném rozmaru při diskuzi o „obchodních záležitostech“ u třetího piva těsně před půlnocí v mé oblíbené restauraci a dostal jsem se tak na tenký led tajících poznatků o stavu akciových trhů. „To určitě, ty Buffete“ opáčil jeden z neméně zdatných znalců tradingového vesmíru a netušil, že svou pochybností vygeneroval základ k následujícím řádkům, které představují práci s hypotézami a jejich aplikaci do života běžného tradera. Něco tvrdit mohu kdykoliv. Dokázat, že tvrzení platí, již vyžaduje jistou námahu, protože důkazní proces bývá většinou náročnější než formulace dokazovaného tvrzení. Nebudu se nyní trápit zbytečnými filozofickými úvahami a logickými jazykovými přesmyčkami a budu se snažit převést svůj náhled na práci s hypotézami pro své vlastní potřeby představující základní práci s daty, které by mohla být vlastní každému obchodníkovi.
Zadaným výrokem o ceně akcie AAPL na úrovni přesně 100 USD jsem nic nepokazil, protože jednoduše nemohu v danou chvíli vědět, jestli to náhodou není pravda, o ceně tohoto technologického titulu nevím téměř nic a můj výrok je tak pravdivý do chvíle, než někdo provede důkaz, že tato má formulace neplatí. Není pak nic jednoduššího než otevřít například nějakou mobilní tradingovou aplikaci a zjistit, že cena této akcie v aftermarketu zakončila na ceně 127 USD. Můj výrok o přesné ceně akcie AAPL vzal za své a bylo potvrzeno, že má hypotéza nyní neplatí. Mohu pak tento proces jednotlivých úkonů zobecnit a využít poznatků teorie statistiky, které pomohou k obecnějšímu pohledu na tento jednoduchý rozhodovací proces. Definice Nulové Hypotézy („Cena akcie AAPL je nyní 100 USD“), stanovení Alternativní Hypotézy („To určitě, ty Buffete“) a provedení testu hypotézy (zjištění dat z mobilní tradingové aplikace) pak položí základ k vyhodnocení, jak by se věci ve skutečnosti mohly mít.
Hypotéza Nula a Alternativní Hypotéza
Vynořit Nulovou Hypotézu (H0) je základem statistického testování hypotéz. Je to tvrzení, přetrvávající stav, výsledek nějakého měření nebo cokoliv jiného, co považuji za platné, pokud nezjistím něco jiného. Mnou proklamované, že akcie AAPL má nyní hodnotu přesně sto dolarů (AAPL = 100 USD) platí, pokud nebude prokázáno, že platí něco jiného, do té doby, z pohledu statistického testování hypotéz, mohu na tomto tvrzení skálopevně trvat. Narážka „To určitě, ty Buffete“ znamená, že můj oponent vytvořil Alternativní Hypotézu (HA) a podstatou tohoto tvrzení je skutečnost, že cena akcie AAPL nyní není přesně 100 USD (AAPL ≠ 100 USD), nic dalšího. Bez Alternativní Hypotézy není co testovat a zkoumat, kdyby tento protipól k nulovým hypotézám neexistoval, vytvořil by se absolutně totalitní svět stojící na tvrzeních nejrůznějších stupňů pravdivosti a kvality, které by nikdo neověřoval a nezpochybňoval (pro některé politiky politický ideál :c). Z pohledu mého zapojení testování hypotéz se formulací alternativní hypotézy vytváří proces porovnávání dvou výsledků nějakého pozorování, například testování nějaké obchodní myšlenky na historických datech, kdy mohu například zkoumat vylepšování zkoumané obchodní strategie úpravou parametrů backtestu, které budu poté poměřovat s nějakou základní obchodní myšlenkou disponující základními zjištěnými vlastnostmi.
Udělat z testování hypotéz statistickou vědu nebylo pro statistiky nic obtížného. Převedením mého problému s tvrzením, že cena akcie AAPL je přesně sto dolarů, do základních možností variant tvorby alternativních hypotéz k této mé nulové hypotéze, mohu vytvořit čtyři základní možnosti, jak se k mé nulové hypotéze postavit a jenom takto jednoduše dojde k slušně rozvětvenému problému. Mohu si tak pro ilustraci představit, že debata u mého stolu by měla pět účastníků (včetně mé osoby), kdy já vytvářím nulovou hypotézu a každý ze zbylých čtyřech účastníků by alternativní hypotézu formuloval jinak, přesto by její potvrzení odmítalo mou nulovou hypotézu. Budeme tak společně hledat co platí, když neplatí má nulová hypotéza. Znění těchto čtyř alternativ by k nulové hypotéze, že cena akcie AAPL je nyní přesně 100 USD bylo následující
A/ Cena akcie AAPL je 115 USD
Alternativní hypotézou by bylo tvrzení, že cena akcie je nyní přesně 115 USD. Znamenalo by to, že pokud bychom prozkoumali aktuální cenu pohledem do obchodní platformy a tato ceny by se nyní nacházela na hodnotě přesně 115 USD, byla by má nulová hypotéza o aktuální ceně akcie na úrovni 100 USD odmítnuta. Z pohledu dokazování a samotné formulace alternativní hypotézy by to v tomto případě nebylo nejšťastnější řešení, mohou ale ve statistické praxi nastat situace, kdy potřebuji rozhodnutí mezi dvěma konkrétními hodnotami, potom by takové znění alternativní hypotézy mělo smysl.
B/ Cena akcie AAPL není 100 USD
Ten, kdo formuluje takto znějící alternativní hypotézu, potřebuje patrně odmítnout nulovou hypotézu bez dalších příkras. Jakákoliv jiná cena akcie než je 100 USD nulové hypotézy vede k jejímu odmítnutí, vyvrátit tak nyní mé tvrzení, že je cena přesně 100 USD by tak nezabralo mnoho času a přemýšlení.
C/ Cena akcie AAPL je vyšší než 100 USD
Alternativní hypotéza představuje tvrzení, že můj parametr 100 USD bude odmítnut ve formulované nulové hypotéze v případě, že cena akcie AAPL bude zjištěna vyšší než je právě těchto 100 USD. Jakákoliv vyšší zjištěná cena než tvrdohlavě prosazovaných 100 USD bude znamenat, že mé tvrzení bude odmítnuto.
D/ Cena akcie AAPL je nižší než 100 USD
Alternativní hypotéza představuje tvrzení, že nulová hypotéza o ceně akcie přesně 100 USD bude odmítnuta v případě, že cena akcie AAPL bude zjištěním prokázána jako nižší než je tvrzených sto dolarů. Pozorovaná cena například 95.45 USD bude znamenat, že mé tvrzení vtisknuté do nulové hypotézy bude odmítnuto.
Je patrné, že mohu k nulové hypotéze naformulovat několik alternativních hypotéz, které mají svůj smysl a které snesou zatížení zkoumáním, které by mohlo mít vztah k nulové hypotéze. V praxi se však v takto jednoduché formě formulace hypotéz nevyskytuje, vše je zpravidla významně složitější. Hypotéza nula bude zpravidla nějaké tvrzení založené na souboru dat, který byl nějakým způsobem analyzován a zpracován a obdařen nějakými výstupními parametry. Alternativní hypotézy pak budou soubory dat vzniklé z pokusů, měření, zkoumání jevů, které formulují nulovou hypotézu a na základě kterých budu chtít platnost této hypotézy přijmout nebo odmítnout.
Na obrázku níže demonstrace jiného příkladu, který podrobím úvaze z naznačených statistických pohledů na testování hypotéz.
Obrázkem jsem chtěl především ukázat, že jsem si zakoupil Apple Pencil, což se výrazně projeví v další grafické úpravě budoucích článků :c). To, že nesmíte nikdy nic absolutně zatracovat, může být vtěleno do populární hlášky: „I rozbité hodiny ukazují dvakrát denně přesný čas“. Na obrázku jsou nefunkční kuchyňské hodiny po zákroku netrpělivého hodináře, které stále ukazují přesně tři hodiny. Nyní, stejně jako v případě neochvějného přesvědčení o ceně akcie AAPL, budu tvrdit, že tyto mé hodiny ukazují přesný čas. Bude to smělá, ale pro mě jediná správná hypotéza (Hypotéza nula), pokud provedeným testováním nedokážu, že to není pravda. Alternativní hypotéza tak bude znít, že tyto hodiny přesný čas neukazují. Jakým způsobem se mohu k řešení takové úlohy postavit?
Testovaný parametr „přesnost hodin“ podrobím zkoumání, nejlépe provedením nějakého způsobu měření času. Mé měření, které se zaměří na pokus vyvrátit nulovou hypotézu, bude spočívat v zaznamenávání času v každou celou hodinu během následujících dvanácti hodin. Jaký bude výsledek? Obdržím celkem 12 výsledků, které budou tvořit „obor hodnot“ testovaného parametru. Tento obor hodnot budou tvořit dvě skupiny výsledků. „Obor přijetí“ bude označovat množinu hodnot, která potvrzuje nulovou hypotézu. Pro testování hypotézy musím vědět, které naměřené hodnoty tuto nulovou hypotézu potvrzují, v komplexnějších úlohách bude vhodné vědět nebo předpokládat, jaké mají hodnoty patřící do oboru přijetí rozdělení pravděpodobnosti. V mém jednoduché případě bude jasné, že pro potvrzení nulové hypotézy bude svědčit hodnota 3:00 hodin. Zbylé hodnoty budou tvořit množinu výsledků nazvanou „kritický obor“ a budou to hodnoty, které budou znamenat zamítnutí nulové hypotézy. Rozdělení výsledků měření do těchto oborů pak bude zejména určovat poznání o vlastnostech dat, potvrzujících nulovou hypotézu.
Pro rozhodnutí, jakým způsobem se k výsledkům postavím, rozhoduje statistický test. Je založen na existenci příslušné statistické funkce, která je schopna stanovit hodnotu testovacího kritéria ze zjištěného vzorku naměřených dat. Tento výpočet, založený na matematickém vzorci popisujícím tuto statistickou funkci, pak bude pro každý jiný způsob měření (různá jiná data) mít odlišné výsledky, mohu tak opakovanými měřeními na různých souborech dat provádět opakované testování hypotéz podle stejného pravidla – statistické funkce. Mohu tak například měřit čas nikoliv pouze za dvanáct hodin, ale za celý týden, mohu zaznamenávat čas nikoliv každou celou hodinu ale každou celou minutu nebo dokonce provádět zcela náhodná měření v nějaké časové periodě. Vždy získám jiný soubor dat, který mohu použít na podporu nebo odmítnutí nulové hypotézy o „přesných hodinách“. Z vypočítané hodnoty příslušné statistické funkce pro daná data pak mohu zjišťovat, jestli patří do některého z oborů, které jsem výše popsal. Pokud vypočítaná hodnota testovacího kritéria padne do kritického oboru, bude to znamenat, že nulovou hypotézu zamítnu, pokud do kritického oboru nepadne, potom nulovou hypotézu zamítnout nemohu.
Vypadá to jednoduše, provedu zadaný statistický záměr nashromážděním potřebných dat, zvolím vhodnou statistickou funkci, která vypočte nějakou hodnotu z takto pořízených dat a budu moci ukončit test rozhodnutím o zamítnutí nebo nezamítnutí nulové hypotézy podle toho, do kterého z oborů vypočítaná hodnota padne. Nesmím ale zapomenout, že posuzuji příslušnost vypočítaného rozhodovacího kritéria nad celým oborem hodnot, který jsem si rozdělil na dvě části a tento obor zahrnuje výsledky podporující obě možnosti, tedy zamítnutí nebo nezamítnutí nulové hypotézy. V mém případě s rozbitými hodinami ukazujícími stále 3:00 hodin je jisté, že zjištěné hodnoty vzorku dat budou kromě jiných údajů také obsahovat také tuto hodnotu.
Rozhodování podle těchto principů, kdy vycházím z celého oboru získaných dat a určím, do kterého z oborů vypočítané testovací kritérium patří, ovšem nemá pouze tyto dvě polohy rozhodnutí. Je zatíženo chybou možné existence části dat, které podporují také opačnou hypotézu, proto mohu tyto chyby rozdělit do dvou kategorií.
Chyba prvního druhu
Pokud ukazují rozbité hodiny přesný čas je nulová hypotéza a pokud by toto opravdu byla pravda a já bych takovou hypotézu zamítnul, dopustil bych se chyby prvního druhu. Mohu si totiž představit, že hodiny sice vypadají nevábně a nehezky, ale mohou být vybaveny ultrapřesným hodinovým strojem ukazujícím přesný čas. Pokud bych v takovém případě Hypotézu nula přesto zamítnul, dopustil bych se chyby prvního druhu. Toto pochybení v odhadu platnosti nulové hypotézy, v mém případě hrubé podcenění výkonnosti mého hodinového mechanismu, bývá označováno ve statistice jako hladina významnosti s označením alfa (α). Hladina významnosti (α) představuje pravděpodobnost, že dojdeme k nesprávnému závěru týkajícího se platnosti nulové hypotézy. Již nyní je patrné, že hodnota alfa by měla být co nejnižší, protože podporuje co nejnižší pravděpodobnost, že uděláme špatné rozhodnutí ve vztahu k nulové hypotéze. Pokud jsem v tomto případě existence nevábných, ale opravdu přesných hodin rozhodl, že ukazují přesný čas, udělal jsem správné rozhodnutí a Hypotézu nula jsem nezamítnul. Tuto pravděpodobnost rozhodnutí mohu vyjádřit jako 1-α a je definována jako spolehlivost testu
Chyba druhého druhu
Zpátky na zem. Rozflákané hodiny zcela jistě neukazují přesný čas, přesto, pokud je vytáhneme k ukázání přesného času v pravý čas, můžeme toto tvrdit. Čas plyne, jenom mé hodiny jej neregistrují, nasbíraná data přesto obsahují některé hodnoty prokazující, že jsou to „dokonalé švýcary“. Pokud je správná alternativní hypotéza, ale přesto padne rozhodnutí, že nezamítám Hypotézu nula, dopouštím se chyby druhého druhu. Pravděpodobnost, že nastane chyba druhého druhu je označováno za beta (β). V případě, že je správná alternativní hypotéza a já jsem zamítnul nulovou hypotézu, udělal jsem správné rozhodnutí, mohu ji poté popsat jako 1-β a tato veličina se nazývá síla testu.
Je jasné, že pravděpodobnosti obou chyb jsou provázané mělo by s nimi být nakládáno tak, aby rozhodování o hypotézách bylo co nejpřesnější, obecně při co nevyšší možné eliminaci obou druhů chyb. Ideální by bylo, aby mé testování bylo zatíženo co nejnižší alfa, tedy mělo nízkou hladinu významnosti (pravděpodobnost, že zamítnu hypotézu nula i když je správná) a současně disponovalo co nevyšší silou testu (1-β), tedy co nejnižší beta (co nejvyšší pravděpodobnost, že zamítnu nulovou hypotézu, protože je správná alternativní hypotéza).
Sladit tyto požadavky v praxi může vyrůst ve slušně rozvětvenou disciplínu. Statistici obvykle volí celkem jednoduchý a praktický přístup, jak posoudit a porovnat výsledky rozličných testovacích úloh. Vychází ze skutečnosti, že primární je stanovit referenční hodnotu hladiny významnosti testu (α) a poté provedené testy, které splňují tuto hladinu významnosti, podrobit zkoumání, který z testů má nevyšší sílu testu (1–β). Nejběžněji je za hladinu významnosti považována úroveň α = 0.05. Protože se situace začíná komplikovat, bude nejlepší se zabývat nějakým konkrétním statistickým příkladem. Tomu by měl předcházet jednoduchý popis kroků a další objasnění souvislostí testovacího procesu.
K zdárnému průběhu testování musím vycházet z několika předpokladů, které určí jednotlivé kroky testování nejrůznějších hypotéz. Zásadním předpokladem je formulace nulové a alternativní hypotézy, to je ale již jasné, protože tyto dvě hypotézy porovnáváme. Důležité je usoudit, jaké mají hodnoty, které zakládají nulovou hypotézu, rozdělení pravděpodobnosti, se kterou se v souboru dat vyskytují . V praxi se budu pravděpodobně potýkat s velkými objemy dat, které budou mít „nějaké rozdělení“, nebude to tedy dvanáct naměřených časů vzorku dat, kterým budu chtít prokázat platnost nulové hypotézy o mých nefunkčních hodinách. Pokud budu znát rozdělení statistických dat (nebo jej smysluplně předpokládat), mohu stanovit testovou statistiku, tedy číslo, které bude signálem, jestli statistický test vyšel významně nebo nikoliv. Významnost testu poměřím s hladinou alfa (α), kterou jsem si stanovil. Budu tak pozorovat, jestli je testová statistika menší nebo větší než zvolená α (nastavena například na úrovni zmiňovaných 0.05) a podle toho rozhodnu o osudu nulové hypotézy. Z tohoto odstavce pak vyplývá, že budu muset rozhodnout, jaké rozdělení mají data nulové hypotézy a poté nasadit správný způsob výpočtu, který rozhodne o jejím osudu. V předchozích článcích (Volatilita a cenový pohyb – I., Volatilita a cenový pohyb – II. a Volatilita a cenový pohyb – III.) jsem vycházel z předpokladu obecného povědomí o normálním rozdělení náhodné veličiny a podcenil jsem zasazení této vědomosti do širšího kontextu statistických znalostí. Pokusím se nyní malou odbočkou toto mírně napravit.
Rozdělení pravděpodobnosti náhodné veličiny
Výsledkem statistického pokusu je zjištění nějaké hodnoty. Budu-li provádět nejrozmanitější měření nejrůznějších jevů, mohu pořizovat data, která mohu dále matematicky a statisticky zpracovávat, k tomu nejméně potřebuji, aby výsledkem každého takového měření nebo pokusu byl údaj, který mohu vybavit číselnou hodnotou a pravděpodobností, s jakou tuto číselnou konkrétní hodnotu nabývá. Podle toho, jakých hodnot může výsledek pokusu nabýt, mohu rozlišit základní dvě skupiny náhodných veličin, tedy číselných hodnost s pravděpodobnostmi, ze kterými své hodnoty nabývají.
Diskrétní náhodná veličina
Provedení pokusu může znamenat, že budu zachytávat stále stejný počet identických hodnot, kterým mohu přiřadit určitou pravděpodobnost svého výskytu. Zapisováním výsledků počtu vytažení jednotlivých druhů karet z piketového balíčku (32 kusů) bych obdržel celkem 32 položek (a nic navíc) a při představě neomezeného počtu pokusů bych došel ke zjištění, že pikovou dámu vytáhnu s pravděpodobností 1/32. Stejnou pravděpodobnost jednotlivého vytažení by pak měly také zbylé druhy karet. Diskrétní (nespojitý) charakter náhodné veličiny pak znamená, že náhodná veličina může nabývat právě pouze těchto 32 hodnot a žádné jiné hodnoty při svém pokus neobjevím. Házením kostky může padnout pouze šest číslic a nestane se, že výsledkem pokusu bude hodnota „čtyři a půl“. Rozdělení pravděpodobnosti diskrétní náhodné veličiny lze popsat dvěma způsoby:
1/ Pravděpodobnostní funkcí, která vyjadřuje, že náhodná veličina X nabude určité hodnoty xi s nějakou pravděpodobností pi, tedy P(X = xi) = pi
2/ Distribuční funkcí, která sděluje, jaká je pravděpodobnost, že hodnota náhodné veličiny X bude menší nebo rovna nějaké hodnotě xi, tedy F(xi) = P(X ≤ xi)
Nejběžnějšími druhy rozdělení pravděpodobnosti diskrétní náhodné veličiny pak může být právě rovnoměrné rozdělení (výsledek hodu kostkou, výsledek vytažení karty…) nebo rozdělení výsledků pokusů, kterými jsou pouze celá kladná čísla, u kterých mohu sledovat pravděpodobnost jejich výskytu, například počet návštěv webu dobretrejdy.com za jeden den, v takovém případě bych mohl uvažovat o Poissonově rozdělení….Diskrétní náhodná veličina a její pravděpodobnostní rozdělení ale nebude patrně předmětem mého dalšího zájmu při práci z daty u mých tradingových úkolů.
Spojitá náhodná veličina
Zjištění, že výsledky pokusů mohou nabývat jakýchkoliv hodnot a těchto naměřených hodnot může být nekonečně mnoho, vede k poznání, že mám co dočinění se spojitou náhodnou veličinou. Mohu pak z těchto výsledků pokusu sestrojit například plynulou křivku do nějakého grafu a zjišťovat, jak nejlépe tuto křivku matematicky popsat. Matematický popis křivky mi pak pomůže zjišťovat, jaké pravděpodobnosti by příslušely jednotlivým hodnotám. Stejně jako u nespojité náhodné veličiny mohu k popisu rozdělení pravděpodobnosti spojité náhodné veličiny použít zápis, kterým vyjádřím:
1/ Hustotu pravděpodobnosti p(x). Zjednodušeně, pokud budu znát hustotu pravděpodobnosti (tedy její nějaký přesný matematický popis), budu moci vypočítat pro jakoukoliv hodnotu mého měření Xi (náhodnou veličinu) její pravděpodobnost výskytu pi.
2/ Distribuční funkcí, která sděluje, jaká je pravděpodobnost, že hodnota náhodné veličiny X bude menší nebo rovna nějaké hodnotě „xi“, tedy F(xi) = P(X ≤ xi). Ze zápisu a logiky sdělení co je distribuční funkce plyne, že pokud budu zjišťovat, jestli je pravděpodobnost výskytu nějaké náhodné veličiny menší nebo rovna nějaké pevné hodnotě, musí být tato pravděpodobnost v intervalu 0% – 100%, matematicky pak mezi hodnotou 0 až 1.
Normální Rozdělení
Nejznámějším rozdělením pravděpodobnosti spojité náhodné veličiny je Normální Rozdělení. Křivka hustoty pravděpodobnosti má zvonovitý tvar (Gaussova křivka). S odkazem na minulý článek pak mohu konstatovat, že k vyčerpávajícímu popisu rozdělení pravděpodobnosti podle Normálního Rozdělení mi stačí znát pouze dvě hodnoty – střední hodnotu a rozptyl. Pomocí těchto dvou hodnot pak mohu určit pravděpodobnost, s jakou se vykytuje určitá náhodná veličina. Definování tohoto rozdělení podle střední hodnoty a rozptylu také znamená, pokud vím, že odmocnina z rozptylu je standardní (směrodatná) odchylka, že k popisu pravděpodobnosti podle Normálního rozdělení mi stačí znát hodnotu střední hodnoty a standardní odchylky. K sestrojení křivky rozložení jednotlivých náhodných veličin potřebuji znát tvar funkce, která tuto křivku popisuje. Tímto vyjádřením je funkce hustoty pravděpodobnosti, která má tento tvar (µ = střední hodnota a δ = standardní odchylka):
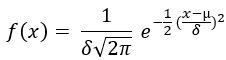
Dosazením hodnoty standardní odchylky a střední hodnoty do tohoto vzorce pak můžu zjišťovat hodnotu funkce hustoty pravděpodobnosti pro libovolnou náhodnou veličinu, která má normální rozdělení s těmito základními parametry střední hodnoty a rozptylu (po odmocnění – směrodatné odchylky). Výše znázorněná funkce tedy představuje hodnoty jednotlivých bodů na této křivce a určuje tak její tvar. Pokud je tedy křivkou hustoty pravděpodobnosti známá zvonovitá křivka (Gaussova křivka), pak znázorněná funkce popisuje tvar (křivku), kterou mohu vykreslit v jednoduchém grafu, jako například v článku Volatilita a cenový pohyb – II.
Zabývat se pravděpodobnostmi jednotlivých výskytů náhodné veličiny, která má Normální rozdělení, však vyžaduje širší úvahu, protože tato pravděpodobnost představuje plochu ve vykresleném grafu Normálního rozdělení pod křivkou hustoty pravděpodobnosti. Velikost plochy pod křivkou nějaké funkce mohu zjistit pomocí integrálu této funkce, mohu tak tímto integrováním získat Distribuční funkci Normálního rozdělení, tato má tento tvar:
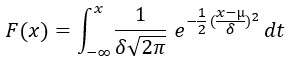
Není zapotřebí nic integrovat ani ručně počítat, je důležité pouze vědět, že se jedná o velikost plochy pod křivkou hustoty pravděpodobnosti a tato celá plocha má velikost jedna. To, že její konkrétní velikost pro nějakou náhodnou veličinu „X“ vypočítám tímto integrálem, tak na to mohu úlevně zapomenout, protože to nebude zapotřebí (existují na to statistické tabulky a samozřejmě Excel). Celá plocha grafu pod funkcí hustoty pravděpodobnosti pak může nabývat hodnot od nuly do jedné, a tento interval reprezentuje pravděpodobnosti od 0% do 100%, něco s výskytem s pravděpodobností 1.30 (130%) jednoduše neexistuje.
Jednoduchý příklad. Má nasbíraná data z měření mají Normální rozdělení se střední hodnotou na vypočítané úrovni 70 a zjištěnou standardní odchylkou ve výši 134. Budu chtít zjistit, pomocí Excelu, s jakou pravděpodobností se v dalším pokusu objeví výsledek s hodnotou menší než je 100. Využiji k tomu přednastavenou excelovskou funkci =NORM.DIST(X; střední hodnota; standardní odchylka, PRAVDA) a výsledkem bude obsah plochy pod křivkou hustoty pravděpodobnosti takto definovaného normálního rozdělení, který bude reprezentovat požadovanou pravděpodobnost.

Výsledkem je, že s pravděpodobností 58.90% se v mém dalším sbírání dat budou objevovat výsledky menší než je hodnota 100. Toto je výsledek operace v Excelu, který za mě provedl výpočet plochy pod křivkou hustoty pravděpodobnosti, nemusel jsem tak řešit žádný integrál. Mohu také usoudit, že se zbylou (100% – 58.90%) pravděpodobností ve výši 41.10% budou výsledky větší než je hodnota 100. Mohu také chtít zjistit, s jakou pravděpodobností se budou objevovat další výsledky v rozsahu 80 – 100. Vypočítám pak stejným způsobem velikost plochy reprezentující pravděpodobnost pro hodnotu menší než 80 a oba výsledky (velikosti ploch) od sebe odečtu, zjistím tak pravděpodobnost výskytu výsledků z intervalu 80 – 100.
Normované normální rozdělení
Neumím a nechci funkce integrovat (vypočítat integrál), a co víc, nepořídil jsem si ani Excel, Vyplývá z doposud napsaného, že jsem vyřízen a musím zkoumání Normálního rozdělení odložit? Nikoliv, stačí, když budu mít po ruce nejběžnější statistické tabulky (například tyto) a mohu získávat stejně plnohodnotné výsledky. Mohu totiž vyjít ze zjištění, že plocha pod křivkou hustoty pravděpodobnosti je vždy rovna jedné, ať se jedná o Normální rozdělení s jakoukoliv střední hodnotou a standardní odchylkou. Tedy i Normální rozdělení, které má střední hodnotu na úrovni nula a standardní odchylku s hodnotou jedna. Takovému Normálnímu rozdělení se říká Normované Normální Rozdělení a plocha pod křivkou hustoty pravděpodobnosti se samozřejmě také rovná jedné. Proč se vlastně zabývat takto „vzácně v přírodě se vyskytujícímu“ rozdělení, když mé měření, které budu v budoucnosti provádět bude zcela jistě nabývat jiných středních hodnot a zcela jiných standardních odchylek (rozptylů)? Ze dvou prozaických důvodů:
1/ Každé Normální rozdělení mohu převést na Normované Normální Rozdělení
2/ Pro Normované normální rozdělení existují statistické tabulky
Pohledem na obrázek níže mohu vypozorovat interpretaci pravděpodobnosti Normálního rozdělení podle standardních odchylek.
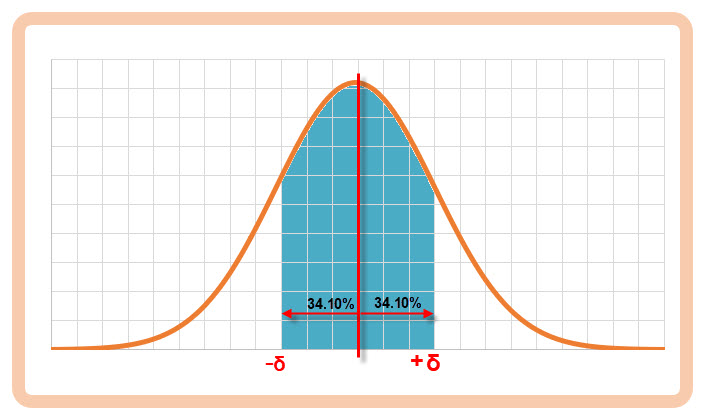
Plocha pod křivkou hustoty pravděpodobnosti Normálního rozdělení, která je vymezena prvními standardními odchylkami (-δ až +δ) má hodnotu 0.682 (68.20%). S touto pravděpodobností mohu očekávat výskyt náhodné veličiny (výsledek měření), pokud má Normální rozdělení. Je tak jedno, jestli má střední hodnotu 70 a standardní odchylku 134 (můj příklad výše) nebo má střední hodnotu nula a standardní odchylku jedna, jako ji má Normované Normální rozdělení, velikost této plochy bude vždy totožná. Zbývá tak jediné, zjistit vztah Normálního rozdělení a Normovaného Normálního rozdělení a nemusím obtížně přemýšlet o náročných početních úkonech. Přestože se to dá matematicky dokázat (tím se nebudu zabývat), tak platí, že pokud mají mé výsledky měření Normální rozdělení, tak pro každý výsledek mého pokusu (náhodnou veličinu) platí, že každá jiná náhodná veličina „U“, která je vypočtena podle stávajících parametrů Normálního rozdělení („X“ hodnota náhodné veličiny Normálního rozdělení, střední hodnota „µ“ a standardní odchylka „δ“) podle tohoto vztahu:
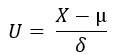
má Normované Normální Rozdělení se střední hodnotou nula a standardní odchylkou jedna. Mohu tak pro jakoukoliv mnou naměřenou hodnotu vypočítat tuto novou „normovanou“ náhodnou veličinu „U“. Proč bych to dělal? Protože její hodnotu znají každé statistické tabulky, nemusím tak nic integrovat ani zapojit Excel a přesto jsem schopen zjistit hodnotu pravděpodobnosti pro jakoukoliv hodnotu náhodné veličiny náhledem do statistických tabulek, a to právě díky takto popsanému „normování“. Mohu pak toto poznání aplikovat na modelový příklad a srovnat oba výsledky.
Má nasbíraná data z měření tedy mají Normální rozdělení se střední hodnotou 70 a standardní odchylkou 134. Budu chtít zjistit, nikoliv pomocí Excelu, ale pomocí statistických tabulek, s jakou pravděpodobností se v dalším pokusu objeví výsledek s hodnotou menší než je 100. Využiji k tomu převod hodnoty náhodné veličiny 100 na normovanou náhodnou veličinu „U“ podle výše uvedeného vzorce:
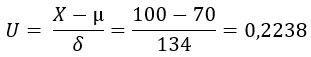
Nyní mohu nahlédnout do statistických tabulek, opět například zde a zjistit, že:
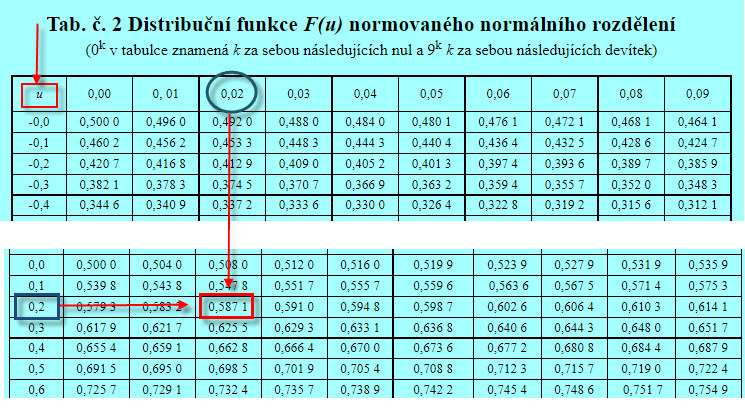
Ve sloupci „u“ pro hodnotu přepočítané normované náhodné veličiny najdu hodnotu 0.2 a pro zjištění jejího přesnější hodnoty (hledám pro hodnotu 0.22) navštívím proto sloupec 0.02 (modrý kroužek). Zjištěná hodnota pravděpodobnosti v buňce tabulek ukazuje hodnotu 0.5871, tedy na hodnotu pravděpodobnosti 58.71%. V porovnáním s excelovskou hodnotou 58.90% jde o nepatrnou odchylku (chtělo by to podrobnější tabulku pro více desetinných míst), výsledná hodnota je tak téměř identická a nemusel jsem nic zadávat do Excelu nebo dokonce integrovat. Mohl bych pak na otázku z modelového příkladu odpovědět se stejnou přesností, jako při řešení pomocí Excelu. Přestože je využití Excelu pravděpodobně elegantnější, musím si uvědomit, že poznatky o rozdělení pravděpodobnosti historicky značně předbíhají vynálezu Excelu nebo jiných statistických aplikací a bylo tak velmi nepraktické vytvářet statistické tabulky pro Normální rozdělení se všemožnými středními hodnotami a standardními odchylkami, převodem na Normované Normální rozdělení je možně použít univerzální jedinou tabulku právě jen pro toto rozdělení se stejným výsledkem.
Centrální limitní věta
Je patrné, že normováním podle určitého matematického vztahu mohu převádět Normální rozdělení na Normované Normální rozdělení a lehce zjišťovat jeho hodnoty. Výsledky jsou pak identické. Pokud budu testovat nejrůznější hypotézy a využívat k tomu vzorky sesbíraných dat, které budu poměřovat s daty podporující nulovou hypotézu, musím mít základní povědomí o tom, jaká mají tato data rozdělení. K vyřešení tohoto problému mohu použít Centrální limitní větu, která tvrdí, ve velmi obecné interpretaci, že po určité úpravě má náhodná veličina Normální rozdělení, jinými slovy můžeme za určitých okolností aproximovat Normálním rozdělením jakékoliv rozdělení. V souvislostí s testováním hypotéz, kdy potřebuji znát rozdělení náhodné veličiny svědčící pro nulovou hypotézu, tak mohu využitím Centrální limitní věty předpokládat, že toto rozdělení bude Normální a mohu je například dále normovat do Normovaného Normálního rozdělení.
Příklad…
Na více než desetiletém období (1.1.2010 – 14.5.2021) jsem aplikoval ve svém excelovském analytickém nástroji historickou analýzu, kdy jsem pořizoval každé pondělí Call Bull Spread s rozsahem tři strike s nakoupenou Long Call opcí „na penězích“ pro podkladový titul SPY, vše s expirací za měsíc. Výsledkem bylo zjištění, že jsem při těchto celkem 590 obchodech průměrně vydělal +54 USD na každém z nich a standardní odchylka mého backtestu měla hodnotu 136. Chci nyní tento test na historických datech vylepšit, proto jsem provedl jednoduché filtrování vstupu do obchodu a tento prováděl pouze v případě, že při vstupu do obchodu byla Implied Volatilita na titulu SPY vyšší než 15%. Slibuji si od tohoto vylepšení zvýšení průměrného profitu, tento jednoduchý filtr pak způsobil, že jsem provedl 246 obchodů, které splnili tuto jednoduchou podmínku.
A/ Zajímá mě nyní, od které výše průměrného profitu na jeden obchod bych mohl se spolehlivostí 95% tvrdit, že se mi podařilo nalézt vylepšení mého základního přístupu.
Má nulová hypotéza tedy proklamuje, že jsem průměrně vydělal +54 USD. Výsledky mých obchodů mají Normální rozdělení se střední hodnotou +54 a rozptylem (1362) 18 496 při 590 obchodech. Má alternativní hypotéza má prokázat, že jsem při filtrování vstupů a provedením 246 obchodů dosáhl významně vyššího zhodnocení prezentované vyšším průměrným obchodem. Pouze na okraj připomínám, že se nyní nezabývám variantami vylepšování backtestu, které vedly k horšímu výsledku průměrného obchodu, než který prezentuje Hypotéza nula, zabývám se pouze výsledky, které vyšly lépe než +54 USD na jeden obchod a hledám odpověď na otázku, jestli je lepší výsledek významný, jedná se tak o „jednostranný test“. Mohu si pak v praxi představit, že mohu testovat hypotézy, kterým bude svědčit nejenom výskyt hodnot významně větších než je hodnota Hypotézy nula, ale také výskyt hodnot, které jsou významně menší než je testovaná hodnota nulové hypotézy, v tomto případě by se jednalo o tzv. „oboustranný test“, pro přehlednost a zachycení jednoduššího významu budu ale dále předpokládat pouze „jednostranné testování“. Není ale nic obtížného rozšířit své poznatky o výpočty oboustranného testu, pokud porozumím logice jednostranného testování, pohledem na obrázek níže s Gaussovou křivkou bych při oboustranném testu „uřízl“ stejný kus plochy také na levé straně obrázku a do výpočtu zahrnul také její existenci…:c)
Hledám tedy, za předpokladu platnosti Centrální limitní věty, hodnotu náhodné veličiny Normálního rozdělení pro pravděpodobnost 95%, Toto Normální rozdělení má střední hodnotu +54 a rozptyl pro 246 obchodů ve výši 18496/246, tedy 75,20 (rozptyl výběrového průměru). Standardní odchylka takového Normálního rozdělení je odmocnina ze 75,20 a má hodnotu 8,67. Pokud bych chtěl zobrazit graficky co hledám, tak by to odpovídalo tomuto:
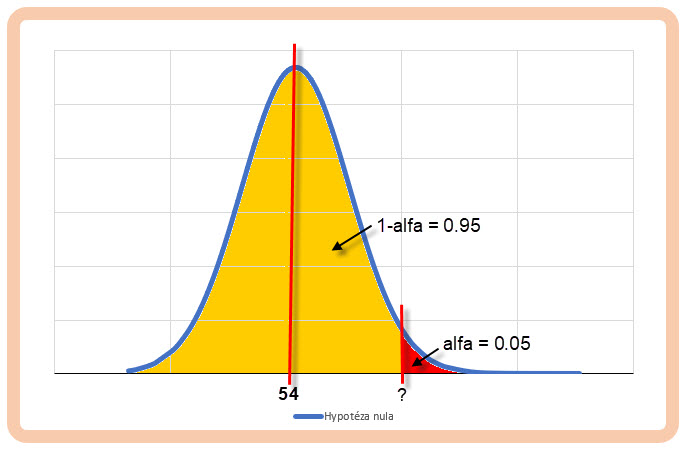
Protože už vím, že mohu využít pro zjištění takové hodnoty v obrázku označené otazníkem Normované Normální rozdělení, budu tedy hledat, jaká je hodnota distribuční funkce Normálního Normovaného rozdělení se střední hodnotou +54 a směrodatnou odchylkou 8.67 při pravděpodobnosti 95% (0.95). Nebudu tedy pomocí této funkce hledat pravděpodobnost, s jakou se vyskytuje náhodná veličina o určité hodnotě, ale zcela naopak, budu hledat, jaká je velikost náhodné veličiny při zadané pravděpodobnosti. Budu tedy statistické tabulky nebo Excel používat „obráceně“, než jsem popisoval v textu výše. Za použití vzorce pro Normované Normální rozdělení:
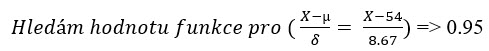
budu hledat ve statistických tabulkách nebo v Excelu hodnotu náhodné veličiny, pro kterou platí pravděpodobnost 0.95.
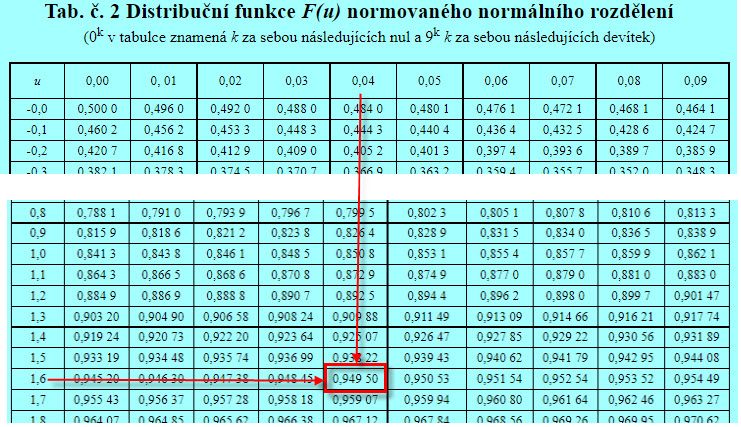
Z tabulek mohu zjistit, že takovou hodnotou je pro Normované Normální rozdělení hodnota 1.64. pro tuto hodnotu pak vypočítám hodnotu, která mi odpoví na mou otázku z příkladu.
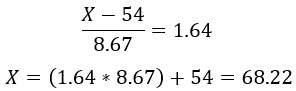
Mohu tak konstatovat, že pro takto nastavený test na historických datech bych mohl za předpokladu, že bude profit průměrného obchodu vyšší než +68.22 USD, zamítnout nulovou hypotézu a konstatovat, že zadaný filtr s Implied Volatilitou vyšší než 15% pomohl nalézt se spolehlivostí vyšší než 95% lepší řešení mého původního zcela mechanického prováděného obchodu.
Tabulky jsou sice dobrá věc, lepší řešení ale nabízí Excel, který umí takové vyhodnocení, tedy hledání „obráceným postupem“, velmi jednoduše pomocí přednastavené formule =NORM.INV(pravděpodobnost; střední hodnota, standardní odchylka)

Excelovská funkce umí takovou „obrácenou záležitost“ po zadání parametrů rozdělení a hledanou pravděpodobnost okamžitě a nemusím nic složitě hledat v tabulkách.
B/ Provedeným vylepšením, filtrováním vstupů do obchodů na Implied Volatilitě podkladu vyšší než 15%, jsem zmenšil počet obchodů na avizovaných 246 obchodů a zjistil, že průměrný profit na obchod činil +70,46 USD. Co mohu z této skutečnosti usuzovat ve vztahu k nulové hypotéze?
Mohu především konstatovat, že pokud k zamítnutí nulové hypotézy se spolehlivostí vyšší než 95% stačí průměrný profit vyšší než +68.22 USD, pak mnou dosažený „vylepšený“ průměrný zisk na jeden obchod ve výši +70.46 USD opravdu potvrzuje zamítnutí nulové hypotézy ve prospěch alternativní hypotézy představované daty z filtrovaného backtestu. Budu si chtít ale úvahu zjednodušit a nehledat nejdříve takto stanovenou mez, tedy hodnotu náhodné veličiny, která mi sdělí, že od této hodnoty již zamítáme/přijímáme nulovou hypotézu (v mém případě je tato mez dána hodnotou +68.22 USD). Budu chtít, pro výsledek mého vylepšeného testu s výsledkem +70.46 USD, okamžitě zjistit, jaká je jeho významnost a nemuset výpočtem zjišťovat nejdříve hodnotu, která tvoří rozhraní mezi oborem přijetí a kritickým oborem a tuto potom porovnat s mým výsledkem provedeného měření, kterým chci zjišťovat nejrůznější domnělá vylepšení oproti nulové hypotéze.
p-value
Takové zjednodušené rozhodnutí mohu provést pomocí p-hodnoty (p-value). Budu jednoduše hledat hodnotu Normálního Normovaného rozdělení pro mnou zjištěný výsledek testu a tento pak poměřovat přímo s hladinou zvolené spolehlivosti (například 0.95). Pro mé rozdělení se střední hodnotou +54, směrodatnou odchylkou 8.67 a se změřenou hodnotou nové střední hodnoty – profitu vylepšeného testu na úrovni +70.46 USD, budu hledat její pravděpodobnost.
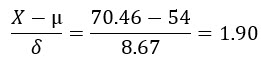
Nahlédnutím do tabulek Normovaného Normálního rozdělení zjišťuji pro hodnotu 1.90 tuto pravděpodobnost:
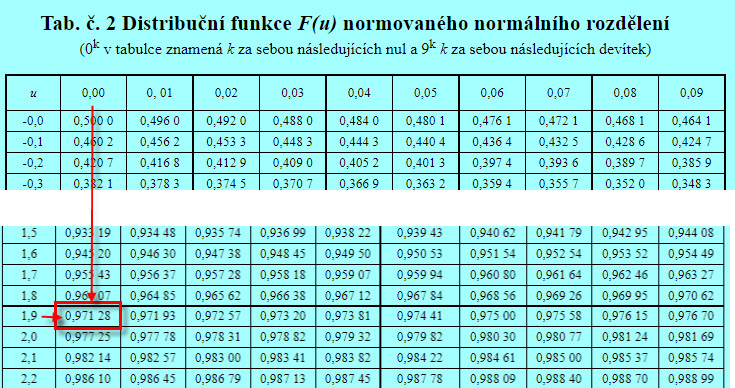
Pozoruji, že mé vypočtené „normované“ hodnotě svědčí ve statistických tabulkách údaj ve výši 0.971, tedy hodnota vyšší, než je spolehlivost ve výši definované 0.95. Zamítám tedy pro tento backtest nulovou hypotézu se spolehlivostí 0.971 a s hladinou významnosti (1-0.971) ve výši 0.029 ve prospěch alternativní hypotézy.
Nebudu chtít využít tabulky, ale zajímá mě, jak si celou věc více zautomatizovat, například pomocí Excelu. Není pak nic jednoduššího, než si p-value vypočítat pomocí distribuční funkce Normovaného Normálního rozdělení. Pro hodnotu 1.90 pak bude tento postup pomocí excelu a výše popisované formule =NORM.DIST, struktura výpočtu by byla následující:
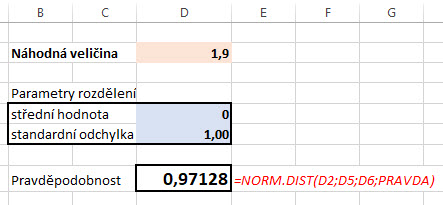
Do připravené tabulky pro výpočet jsem zadal parametry Normovaného Normálního rozdělení se střední hodnotou nula a standardní odchylkou jedna a vyšel mi stejný výsledek pro spolehlivost ve výši 0.971. Mohu tak provést stejnou interpretaci, jako u výsledku pomocí statistických tabulek.
Zdálo by se, že uvedený příklad je jednoduchý. Jednoduchou úpravou jsem dosáhl lepšího výsledku průměrného obchodu, ovšem také jsem provedl méně obchodů. Méně obchodů znamená menší celkový profit za testované období. Z tohoto pohledu je již těžší se rozhodnout, který z výsledků je vlastně lepší a vodítkem k rozhodnutí může být, mimo jiné, takto sestavené posouzení obchodního problému. Na obrázku níže je equity křivka (modrá křivka) pro data, které zakládají nulovou hypotézu a výsledek vylepšeného filtrovaného testu se vstupy uskutečněnými pouze při Implied Volatilitě vyšší než 15% (hnědá křivka).
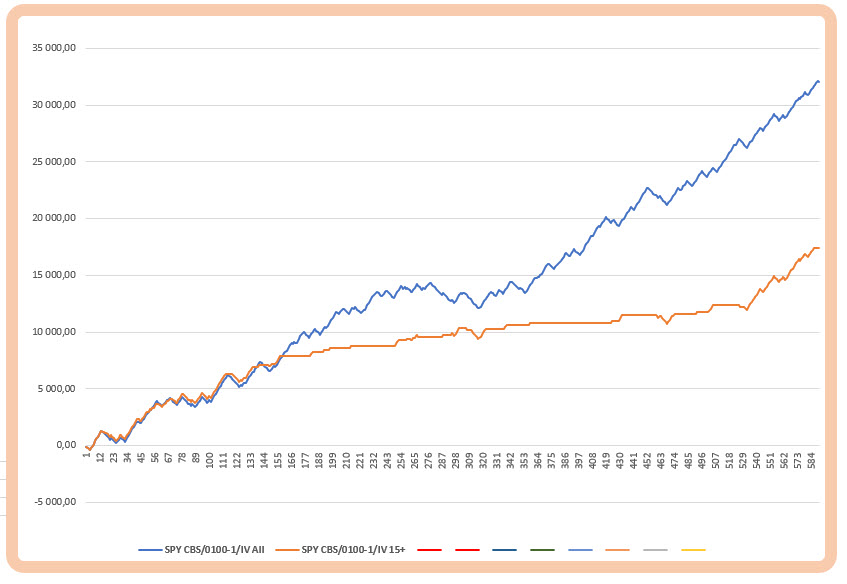
Souhrn obou analýz v histogramu
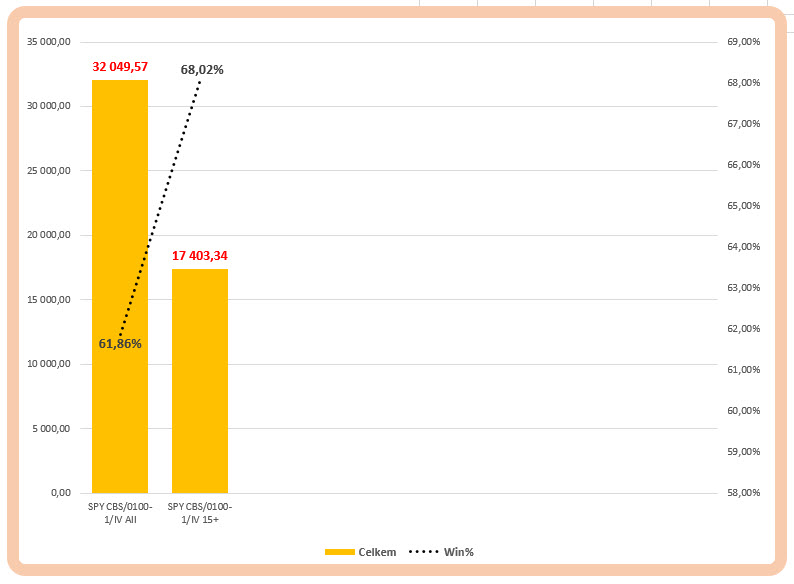
Pravý sloupec s nižší celkovou equity díky menšímu počtu realizovaných obchodů (o polovinu méně) s vyšším procentem vítězných obchodů reprezentuje Alternativní hypotézu, levý sloupec je původní neupravovaná strategie mechanického nakupování představující Hypotézu nula.
Problematika testování hypotéz může nabídnout velmi efektivní pohled na výsledky mých pokusů a jejich interpretaci. Tato část statistické vědy je značně rozsáhlá a nabízí daleko více možností, jak k vyhodnocení mých testů na historických datech mohu přistoupit než jen velmi obecný pohled na tuto problematiku v řádcích výše. Základním motivem poznat tyto statistické metody by mohla být skutečnost, že při obrovských objemech analyzovaných dat, kterými se budu snažit potvrdit nebo odmítnout nulovou hypotézu, nemohu zcela jednoznačně a na první pohled usoudit, co pro potvrzení původních tvrzení svědčí a co nikoliv. Výše uvedené řádky jsou pouhým střípkem z obrovské mozaiky statistických přístupů, které mohu na svá analyzovaná data použít a měly by být například inspirací, jak se k vyhodnocování mých zamýšlených obchodních přístupů postavit.
Komentáře a příspěvky k tomuto článku prosím směrujte do Diskuzního fóra do tohoto vlákna :c)
Sleduj facebook, napiš e-mail nebo tweet