Používání zaběhlých hovorových frází je součástí běžné každodenní komunikace, nevyhýbá se tak ani obchodníkům, kteří používají obchodní výrazy či slovní spojení, jejichž pochopitelnost a zaběhlá platnost se pak bere za jakousi „jasnou věc“. Tyto traderské axiomy popisují běžné obchodní jevy nebo stavy, o jejichž významu se pak nepochybuje, „…návrat k průměru…“, „…ceny jsou rozptýleny kolem střední hodnoty…“, „..hodnota akcie se odchyluje od…“, „…tyto akciové indexy spolu významně korelují…“ atd., jsou natolik běžné výroky, že jejich podstatu již patrně nemusím nijak objasňovat, přestože mi mohou být některé souvislosti, příčiny nebo důsledky skryty v oparu jakéhosi příjemně nepoznaného nevědomí. Čím vyšší četnost používání těchto slovních spojení, která mě nenutí nikdo objasňovat, tím vyšší ubezpečení, že je vše v pořádku a že jsou zřejmé alespoň triviální souvislosti a povědomí o pronášených slovech. Nevím, jestli je tomu opravdu tak a nejsem si úplně jistý, jestli základní povědomí o nejběžnějších matematických a statistických výrazech je natolik vžité, aby nezkreslovalo jejich podstatu a nakonec také jejich interpretaci. Pokusím se v tomto článku shrnout a popsat základní souvislosti nejběžnějších matematicko-statistických výrazů, nejen jako úvod k avizovaným článkům o Market-Neutral obchodnímu přístupu, ale také jako obecnější příspěvek k popisu základních statistických jevů, se kterými by se mohl každý běžný obchodník při vlastním zkoumání zákonitostí finančních trhů setkat.
Datové body
Nejběžnější matematicko-statistickou zápletkou by mohlo být základní hledání vztahu jednotlivého datového údaje k nějaké „běžné hodnotě“ pozorované datové řady, jejíž je součástí. Záměrně se nyní vyhýbám slovu „průměr“, protože tento pojem může mít několik rozměrů. Podstatou mnoha obchodních strategií je tzv. „mean reverting“ chování datových řad (například ceny investičního nástroje) a jeho podstatou by mělo být spoléhání se na skutečnost, že trhy nerady setrvávají na výjimečných hodnotách a chtějí se chovat „normálně“, tedy se svých maxim sestupují na nějaké své běžné hodnoty nebo své poklesy nakonec kompenzují posilováním na své „normální“ hodnoty. Běžná, obvyklá nebo normální hodnota je pak to, co by měl takto zaměřený obchodník hledat a zamyslet se, jaký je vztah každého datového bodu k takto zjištěné „běžné hodnotě“ a jak jej popsat. Na obrázku níže jsou dvě řady čísel, které mohou reprezentovat například měsíční uzavírací ceny dvou pomyslných akciových titulů.

Budu se nyní snažit vyhodnotit tyto dvě datové řady z pohledu rozložení jednotlivých hodnot v každé z nich. Toto rozložení pak bude charakterizováno identifikací polohy každého prvku datové řady vzhledem ke své obvyklé (nejběžněji střední) hodnotě. Musím se tak nejdříve mírně zabývat, jaké náhledy na tuto střední hodnotu se mi nejběžněji nabízí.
Modus (Mode)
Přestože to může vypadat podivně a neprakticky, budu moci svou pozornost při hledání normálních hodnot zaměřit na získání přehledu, které číslo se v každé datové řadě vyskytuje s největší četností. Bude mě tak zajímat nejčastěji se vyskytující hodnota, které by mohla ukázat první základní pohled na datovou řadu, tedy konstatování, že co je nejběžnější by také mohlo být nejnormálnější, těmto číslům s největším počtem výskytů v datové řadě se říká modus.

V první datové řadě se dvakrát objevuje číslo 105, proto modus této datové řady je pak právě 105. Druhá datová řada nemá ani jeden údaj zastoupen více než jednou, každá hodnota ve vzorku dat je originál a mohu o této druhé datové řadě prohlásit, že hodnota parametru modus nebyla nalezena. Zjištění hodnoty pro modus v horní datové řadě dává zcela jednoduchý a základní pohled na analyzovaný datový soubor a může poskytnout první náhled na nasbíraný vzorek dat, jednoduše zjistím, která hodnota se vyskytuje v datové řadě nejčastěji a na tuto mohu upřít svou první pozornost, jako na pokus o hledání „normální hodnoty“. První logický zádrhel pak samozřejmě nastane, pokud se žádná hodnota v datové řadě neopakuje (viz druhá datová řada) nebo pokud se ve vzorku zkoumaných dat objevuje některá stejná hodnota se stejným počtem četností, může se pak stát, že kromě výskytu dvou hodnot 105 se vyskytnou také dvakrát hodnoty 107. Musím pak vyhodnotit, že zkoumám tzv. bimodální datovou řadu se dvěma hodnotami pro modus na úrovni 105 a 107. Další komplikací pak je, pokud mám těchto hodnot pro modus několik, třeba několik stovek, je tak patrné, že hledání normálních hodnot pomocí statistického nástroje modus nebude pro mé ceny akcií patrně nejvhodnější nástroj, může však skvěle posloužit pro jiné vyhodnocení datových souborů pro jiné statistické potřeby. V Excelu (verze 2010 a vyšší) je hledání hodnoty modus zabezpečeno funkcí =MODE.SNGL, v případě, že modus neexistuje, vrací toto zjištění do buňky hlášením „#NENÍ_K_DISPOZICI“, pokud je nalezeno více hodnot pro modus (bimodální, trimodální…multimodální datové řady), je zobrazen modus pro první nalezenou hodnotu ve sledované oblasti, pokud bych potřeboval zjistit všechny nalezené hodnoty, musel bych využít maticovou funkci Excelu =MODE.MULT
Medián (Median)
Hledání mediánu nasbíraného vzorku dat je zcela jinou disciplínou, než pozorování počtu četnosti výskytů stejných hodnot v případě hodnoty modus. Medián je hledání takové hodnoty v souboru dat, která rozdělí zkoumaný soubor dat na stejné poloviny, kde je poté polovina dat s nižší hodnotou, než je hodnota mediánu a druhá polovina dat má vyšší hodnotu než medián. Rozdělení datové řady na takto shodné poloviny již může dávat smysl pro představu, jaká je hodnota tohoto „dělícího bodu“, tedy hodnotu mediánu. Při hledání mediánu vzniká zásadní problém při hledání této „dělící hodnoty“ v počtu dat v analyzované datové řadě. Ideálním stavem je situace, kdy má datová řada lichý počet údajů, potom mohu tento medián velmi pohodlně nalézt pouhým seřazením hodnot od nejnižší k nejvyšší (nebo od nejvyšší k nejnižší) a takto rozdělit analyzovaný soubor dat na dvě přesné poloviny, při počtu dat označených jako „n“ pak bude pro určení pořadí stačit výpočet (n+1)/2. Jedenáctka fotbalistů seřazená podle velikosti od nejmenšího k nejvyššímu při hledání mediánu výšky mančaftu pak při výpočtu (11+1)/2 ukáže na šestého kopálistu v řadě, který tvoří toto rozhraní, pět spoluhráčů na jedné straně řady bude nižších a pět spoluhráčů na druhé straně řady bude vyšších. V případě vzorových dvou řad z mého příkladu pak bude druhá řada, která má lichý počet členů (sedm), mít tento medián

Při počtu dat sedm (n = 7) je po provedeném výpočtu (n+1)/7 zjištěno, že hodnota mediánu je hodnotou na čtvrtém místě mé seřazené datové řady, medián má hodnotu 81. V datové řadě se pak vyskytují tři čísla s nižší hodnotou a tři čísla s vyšší hodnotou.
Při hledání mediánu v případě sudého počtu zkoumaných dat je postup založený na stejné logice, tedy hledání hodnoty „dělícího bodu“, po jehož nalezení budu moci pozorovat polovinu hodnot nižších než medián a polovinu hodnot vyšších než medián. Musím se však smířit s konstatováním, že hodnota mediánu nebude přesně odpovídat některému z členů datové řady, ale že po seřazení analyzovaných dat podle velikosti bude mediánem průměr mezi dvěma hodnotami, které se budou nacházet uprostřed hodnot takto seřazeného souboru. Kompletní šestka hokejistů i s brankářem nacházející se aktuálně na ledě a seřazených podle velikosti by při hledání mediánu výšky musela vzít za vděk výpočtem, který by vycházel z průměru výšky třetího a čtvrtého hokejisty v řadě, někde mezi nimi by se nacházela hodnota mediánu, aby nalevo od této hodnoty byli tři hokejisté menšího vzrůstu, než je hodnota mediánu a napravo od mediánu by se nacházeli tři hokejisté vyššího vzrůstu. Vypočítanou hodnotou mediánu by tak nebyl obdařen žádný z konkrétních hráčů, bylo by to pouze vypočítané průměrné číslo nacházející se mezi prostředními dvěma seřazenými hokejisty. Na obrázku níže je výpočet mediánu mé vzorové řady o sudém počtu členů.

Zjištěný průměr prostředních dvou členů seřazené řady podle velikosti jednotlivých dat v datové řadě stanovuje hodnotu mediánu na 100.50. V osmičlenné datové řadě jsou pak čtyři hodnoty menší než 100.50 a čtyři hodnoty vyšší než 100.50.
Využití mediánu jako hodnoty charakterizující nějakou obvyklou hodnotu sledovaného datového souboru může poskytnout dobrý základní náhled na strukturu a rozložení analyzovaného souboru, zejména z pohledu extrémních hodnot, které by se mohly ve vzorku dat nacházet, a které by mohly být při posuzování jinými jednoduchými statistickými metodami zkresleny. Na obrázku níže je opětovné vyhodnocení hodnoty mediánu a k němu stanovena hodnota aritmetického průměru vzorku dat

Mohu pozorovat, že při hodnotě mediánu s hodnotou 81 je průměrná hodnota analyzovaných dat na úrovni 100. Mohu však datovou řadu vybavit extrémní hodnotou a poté zkoumat, jak se jednotlivé hodnoty změní.

Poslední hodnotu v datové řadě na úrovni 220 jsem nahradil extrémní hodnotou 3250. Mohu pak vypozorovat, že hodnota mediánu zůstala stejná, protože se tato extrémní hodnota nachází opět ve stejné polovině dat vyšších než medián bez ohledu na její velkost a nic dalšího se nezměnilo, hodnota aritmetického průměru však touto extrémní hodnotou vykázala značné zkreslení a vyhoupla se na více než pětinásobek původního průměru, z původní hodnoty 100 se zvedla na hodnotu 528.
V běžné praxi pomocí Excelu nebudu muset nic seřazovat podle velikosti ani vyhodnocovat, jestli mám lichý nebo sudý počet jednotlivých datových položek. Funkce =MEDIAN se zahrnutou oblastí buněk obsahující analyzovaná data vyhodnotí hodnotu mediánu bez jakýchkoliv dalších úprav.
Aritmetický průměr (Arithmetic Mean)
Po zjištění, jaká hodnota se vyskytuje ve sledované řadě nejvícekrát (modus) nebo prozkoumání, jaká hodnota reprezentuje střed hodnot sledované řady tak, že ji rozděluje na stejně početné poloviny výskytů podle své velikosti (medián) mohu za hledání střední hodnoty, průměru, nejběžnější hodnoty, průměrné hodnoty nebo obecně „meanu“ považovat hodnotu vypočítanou jako aritmetický průměr hodnot analyzované datové řady. Nebudu nyní urážet čtenářovo ego popisováním struktury výpočtu aritmetického průměru, protože sečíst všechna čísla a vydělit tento součet počtem sečítaných hodnot je úkol z prvního stupně základní školy
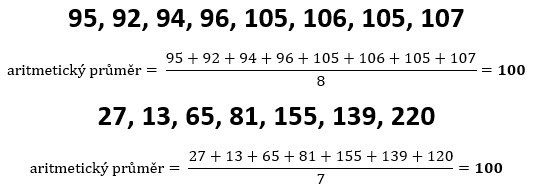
Provedená matematická operace na obou datových řadách ukazuje, že aritmetický průměr je v obou případech stejný a má hodnotu 100. V Excelu je pak pro výpočet aritmetického průměru určena funkce =PRUMER na označené oblasti buněk, obsahující data, která chci zprůměrovat. Výpočet aritmetického průměru tak není nic vědeckého. Nejjednodušší a nejznámější způsob, jak nalézt střední hodnotu metodou aritmetického průměru je pak opravdu nejběžnější přístup, kterým mohu na analyzovaných datech vyhledat hodnotu „meanu“, ve většině případů je pak za vypočítanou hodnotou „středu“ datové řady považována právě tímto jednoduchým způsobem vypočítaná hodnota.
Variační rozpětí (Range)
Pokusit se rozpoznat základní vlastnosti polohy jednotlivých dat zkoumaných datových souborů pomocí zjištění „nějaké střední hodnoty“ je prvním dobrým krokem, jak získat základní a smysluplný parametr. Zjištění hodnoty aritmetického průměru pro obě sledované datové řady na hodnotě 100 ale v žádném případě není nic, co by mě mělo uspokojit, protože tato hodnota v žádném případě nepopisuje rozptýlenost jednotlivých dat kolem této střední hodnoty, pouhé konstatování, že oba datové soubory mají stejnou střední hodnotu, kolem které se vše „nějak odehrává“, by zcela jistě byla chyba, které je patrná z grafického pohledu na obě datové řady v jednoduchém diagramu.
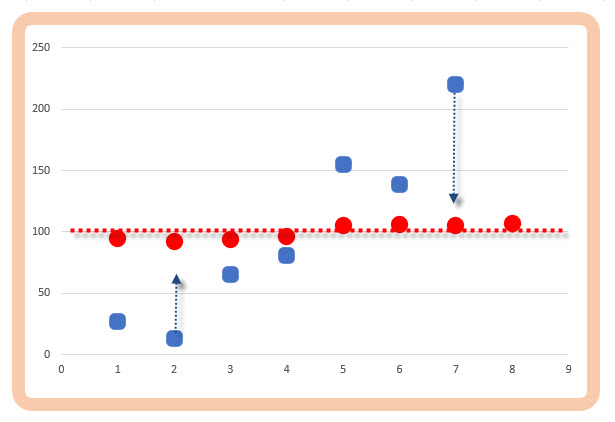
Je patrné, že jednotlivé datové údaje z horní řady seřazených dat, kterou reprezentují červené body, jsou velmi úzce rozptýleny kolem průměrné hodnoty na úrovni 100, kdežto modré čtverečky reprezentující spodní řadu seřazených dat se stejným průměrem na hodnotě 100 jsou zásadněji a viditelněji vzdáleny od této průměrné úrovně. Tento výrazný a viditelný nepoměr v umístění jednotlivých dat vzhledem ke své střední hodnotě – aritmetickému průměru – mohu nejjednodušeji popsat hodnotou Variačního rozpětí, tedy výpočtem velikosti rozdílu nejvyšší a nejnižší hodnoty nacházející se v analyzovaném datovém souboru

Z obrázku vyplývá, že přestože střední hodnota obou souborů je 100, hodnoty, ze kterých výpočet „meanu“ byl stanoven, disponují značně odlišným variačním rozpětím. První datová řada (červené body na diagramu) má téměř čtrnáctkrát menší Variační rozpětí než řada reprezentující modré body na diagramu. Mohu tedy kromě vypočtené hodnoty středu datových souborů využít první pomůcky pro určení polohy zbylých dat ve vztahu k vypočítané střední hodnotě, kterou bych mohl alespoň velmi zjednodušeně zobrazit míru, se kterou se jednotlivá data přimykají ke své střední hodnotě, je jasné, že větší „nedomykavostí polohy“ jednotlivých dat disponuje analyzovaný datový soubor s nepoměrně vyšším variačním rozpětím. Nevýhodou zaměření pozornosti na hodnotu variačního rozpětí může mít opačné zjištění, kdy datové soubory mohou mít stejně veliké (nebo velmi podobné) variační rozpětí, ale hodnoty středních hodnot budou diametrálně odlišné a nabízet zkreslující interpretace.
Excel umí vyřešit zjištění variačního rozpětí velmi banálním způsobem, kdy pomocí funkcí =MAX a =MIN pro analyzovanou oblast dat zjistím takto hledané datové položky, jejich prostý rozdíl pak bude hodnotou variačního rozpětí.
Rozptyl (Variance)
Zjistit střední hodnotu datového souboru a rozsah, ve kterém se jednotlivá data nacházejí je zajisté užitečné zjištění. Více mě však bude zajímat, jak stanovit míru rozložení analyzovaných dat vzhledem ke střední hodnotě v rámci zjištěného variačního rozpětí, tedy kvantifikovat číslem míru rozptýlenosti dat. Základním parametrem, který má statistika k dispozici je možnost vypočítat tzv. rozptyl. Přestože by se nabízelo jednodušší řešení, jak stanovit základní parametr polohy každého z členů datového souboru vyhledáním průměru vzdálenosti každé hodnoty datové řady ke střední hodnotě, k výpočtu hodnoty rozptylu bylo použito průměrování „čtverců vzdálenosti“ každé naměřené hodnoty ke střední hodnotě. Není to nic nepředstavitelného, naměřenou vzdálenosti každé zjištěné hodnoty v datovém souboru ke střední hodnotě umocním na druhou a z těchto mocnin pak vypočítám aritmetický průměr vydělením počtu zjištěných „čtverců hodnot“.
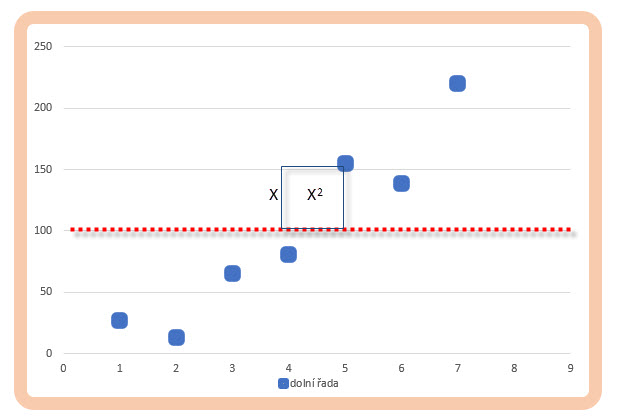
Protože u modelových řad z řádků výše již vím, že hodnota průměru je 100, budu jednoduše zjišťovat, jaká je vzdálenost každého člena mého analyzovaného souboru od tohoto průměru a tuto vzdálenost umocním na druhou. Z naměřených mocnin pak vypočítám aritmetický průměr, kterým určím číslo znamenající hodnotu Rozptylu. Hodnota rozptylu se označuje jako δ2, budu se tak zavedeného značení držet také. Na obrázku níže je naznačen výpočet rozptylů obou sledovaných datových řad.

Výpočet vzdálenosti každého bodu od střední hodnoty, umocnění této vzdálenosti ke střední hodnotě na druhou a výpočet průměru ze získaných mocnin dává hodnoty rozptylu pro obě datové řady. Mohu konstatovat, že řada, která měla velmi úzké variační rozpětí má hodnotu rozptylu δ2 = 35, kdežto rozptyl datového souboru s širokým variačním rozpětím má hodnotu rozptylu δ2 = 4776. Mohu tak konstatovat, že průměrný čtverec vzdálenosti datového bodu od střední hodnoty je pro první analyzovanou řadu na úrovni 35 resp. 4776 u druhé analyzované datové řady. Přestože jsou čísla diametrálně odlišná, je velmi nepraktické si za těmito čísly něco představit, samozřejmě pominu-li základní zjištění, že jsou významně jinak veliká. Pokud bych setrval v představě, že každá z datových řad představuje například měsíční uzavírací ceny akciových titulů, pak bych musel konstatovat, že například u druhé datové řady je průměrná hodnota druhé mocniny vzdálenosti ceny akcie na konci měsíce vzhledem k její „normální hodnotě“ na hodnotě 4776.
Velmi jednoduše mohu vypočítat hodnotu rozptylu pomocí Excelu. Funkce =VAR.P pro značenou oblast analyzovaných dat vrátí hodnotu hledaného rozptylu, nemusím tak tuto operaci provádět ručně po jednotlivých krocích pro každý datový bod mého datového souboru, což by bylo velmi úmorné
Standardní odchylka (Standard Deviation)
Zjistit jakousi průměrnou vzdálenost každého z členů analyzovaného datového souboru od její střední hodnoty již umím pomocí rozptylu (δ2), tento mi však udává, jaká je průměrná hodnota čtverce této průměrné vzdálenosti, což je, jak jsem již výše konstatoval, velmi nepraktické a vyžaduje vyšší míru představivosti. Chci po svých výpočtech, aby ukazovaly pochopitelné a snadno interpretovatelné hodnoty. Pokud tedy vím, jaká je průměrná hodnota čtverce vzdálenosti od střední hodnoty (toto mi udává rozptyl δ2), není nic jednoduššího, než pouhým odmocněním této hodnoty rozptylu získat jednoduchou bezrozměrnou hodnotu této průměrné vzdálenosti. Odmocněním hodnoty rozptylu získám hodnotu Standardní odchylky, ze čtverce vzdáleností dostanu obyčejnou vzdálenost, tedy hodnotu strany tohoto čtverce.
![]()
Uvedený vzorec je demonstrací takto jednoduchého výpočtu Standardní odchylky, kterou upravuji hodnotu rozptylu na jednorozměrné a jednoduché číslo, které mohu interpretovat v původních jednotkách analyzovaného datového souboru a nemusím trápit představivost „čtvercem vzdálenosti“. Hodnota standardní odchylky mi tak ukazuje, jaká je průměrná vzdálenost bodů analyzované datové řady ke střední hodnotě.

Odmocněním hodnot rozptylu svých modelových datových souborů pak mohu zjistit, jaké jsou tyto průměrné vzdálenosti. Pokud bych si tedy opět představil, že obě datové řady představují dolarové závěrečné ceny akcií pro poslední dny minulých měsíců, mohu konstatovat, že pro horní řadu závěrečných měsíčních cen platí, že jednotlivé ceny jsou od střední hodnoty 100 USD vzdáleny průměrně 5.92 USD a pro spodní řadu závěrečných měsíčních cen platí, že tyto měsíční zavírací ceny jsou od střední hodnoty na úrovni stejných 100 USD průměrně vzdáleny 69.11 USD. Toto je již velmi pochopitelný a interpretovatelný výsledek, který dává zcela zřetelnou představu, jakým způsobem jsou data rozptýlena vzhledem ke své střední hodnotě. Pokud bych předpokládal nákup akcie za 100 USD, mohu tak očekávat, vycházeje z historického vývoje podle sebraných dat, že průměrný měsíční pohyb akcie v prvním případě může být +/-5.92 USD nebo +/- 69.11 USD v druhém případě. Zcela zřetelně je pak patrné, že nákup druhé akcie s větší Standardní odchylkou mi patrně připraví více horkých chvilek než pořízení akciového titulu s menší Standardní odchylkou.
Excel samozřejmě disponuje funkcí pro výpočet Standardní odchylky, kterou je =SMODCH.P s výběrem oblasti, pro kterou chci tuto hodnotu zjistit. Protože je to druhá odmocnina z rozptylu, můžete vyzkoušet zjistit nejdříve tuto hodnotu rozptylu z analyzovaných dat (=VAR.P) a tuto hodnotu pokusně odmocnit třeba kalkulačkou, výsledkem je pak stejná hodnota jako zjištěná pomocí funkce =SMODCH.P.
V článcích Volatilita a cenový pohyb – I. nebo Volatilita a cenový pohyb – II. jsem pak rozváděl téma Standardní odchylky ve vztahu k pravděpodobnostem za předpokladu, že analyzovaná data mají Normální rozdělení a jaké další statistické ukazatele mohu na zkoumání takového datového souboru použít a co by mi mohly o analyzovaných datech prozradit.
Doposud jsem statistické ukazatele použil pro zkoumání polohy jednotlivého datového bodu mého datového souboru, tedy jakým způsobem mohu najít a kvantifikovat jeho polohu ve vztahu ke střední hodnotě, tato střední hodnota pak byla popsána možností zvolit její určení pomocí hodnoty vypočítané jako modus, medián nebo aritmetický průměr. Za nejjednodušší a nejvhodnější výpočet střední hodnoty jsem shledal právě aritmetický průměr a k jeho hodnotě jsem pak hledal průměrnou vzdálenost dat pomocí dalších výpočtů. Variační rozpětí mi bylo schopné definovat, jakou „šířku“ každý analyzovaný soubor může mít, o průměrné poloze datového údaje tvořící datový soubor to však neřeklo téměř vůbec nic. Rozptyl, jako statistická veličina založená na určení mocniny (čtverce) vzdálenosti každého jednotlivého datového údaje od střední hodnoty, která následně zprůměrována udávala průměrnou velikost druhé mocniny takové průměrné vzdálenosti, což se zase ukázalo nepraktické pro představivost v původních jednotkách měření nebo získávání jednorozměrných dat namísto jejich druhých mocnin. Prostým odmocněním hodnoty rozptylu jsem ze „čtverců udělal strany“, tedy vrátil výpočtu průměrné vzdálenosti datového bodu od střední hodnoty pochopitelné a srozumitelné číslo, tato statistická veličina je nazvána Standardní odchylka. Toto jednoduché shrnutí, jehož výstupem je pak schopnost vypočítat průměr (střední hodnotu), rozptyl a standardní odchylku jakékoliv datové řady bude základním kamenem poznání základních statistických ukazatelů vztahů mezi jednotlivými datovými řadami.
Datové řady
Zkoumání vlastností datového souboru mohu nyní rozšířit o pozorování dvou a více sérií nasbíraných dat a zjišťovat, jaký mají tyto datové soubory vzájemný vztah. Omezím se nyní pouze na časové datové řady, tedy na datové soubory, u kterých mohu určit, že v určitém okamžiku jsem schopen definovat hodnotu datového bodu pro každý datový soubor a aby to bylo ještě jednodušší, budu pracovat se dvěma datovými soubory. Praktickou ukázku grafického zobrazení existence dvou časových datových řad mohu pozorovat na obrázku níže.
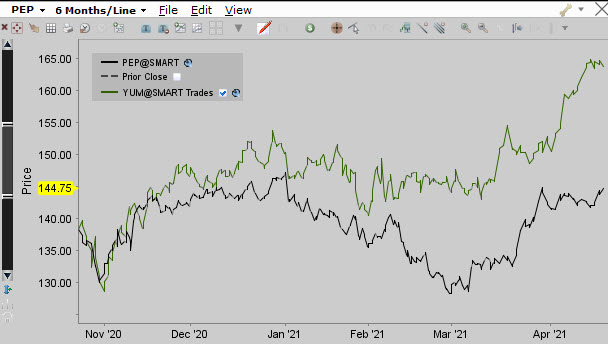
Půlroční cenový průběh vynesený v grafu představuje hodnotu akciových titulů PEP a YUM. Nemohu si nevšimnout, že přestože jsou obě křivky průběhu originální, je prostým okem pozorovatelný vzájemný vztah obou těchto cenových křivek. Mohu tak v obecné rovině konstatovat, že oba datové soubory – cenové datové řady, mohou odrážet jakýsi vzájemný vztah, a tento vzájemný vztah se budu snažit co nejjednodušeji kvantifikovat. Nebude mě nyní zajímat, jestli je mezi oběma datovými soubory nějaká kauzalita, tedy jestli jsou cenové pohyby reakcí na společné fundamentální události nebo jestli existuje přímá interakce mezi oběma časovými řadami navzájem. K pouhému základnímu prozkoumání vzájemného vztahu použiji opět jednoduché statistické nástroje, postavené na statistických výpočtech vycházejících z textu výše
Kovariance (Covariance)
Poznat metodu výpočtu, který definuje hodnotu kovariance, mohu odtušit již z názvu tohoto statistického výrazu. Pokud jsem u kvantifikace hledání průměrné velikosti polohy datového bodu ke střední hodnotě použil výpočet rozptylu (variance), bude hledání hodnoty kovariance dvou datových řad znamenat poznání a změření „co-variance“, tedy jakéhosi „spolu-rozptýlení“ jednotlivých souvisejících datových položek. Stanovení rozptylu pro jeden datový bod určením jeho vzdálenosti od vypočítané střední hodnoty a umocněním na druhou (tedy čtverec vzdálenosti) nachází využití také ve stanovení hodnoty kovariance dvou datových řad. Také budu tedy hledat vzdálenosti jednotlivých datových bodů od střední hodnoty, jenom to budu provádět současně dvakrát, pro každou z obou datových řad. Pokud jsem výsledný rozptyl pro jeden datový bod pro jednu datovou řadu, jako ukazatel průměrné vzdálenosti ke střední hodnotě, zjistil z aritmetického průměru všech zjištěných a vypočítaných čtverců hodnot, bude hledání hodnoty kovariance téměř identické a bude obsahovat nalezení aritmetického průměru ze všech součinů vzdáleností každého datového bodu ke střední hodnotě pro každou datovou řadu. Jak to může vypadat s kovarianci prakticky můžu ukázat opět na dvou modelových časových datových řadách reprezentujících například konečné měsíční ceny dvou akciových titulů za posledních osm měsíců.

Obě časové řady mají osm datových prvků, akcie A má střední hodnotu na úrovni 100 (1), vypočítanou jako aritmetický průměr, stejným způsobem je stanovena střední hodnota pro akcii B, která činí 105 (2). Matematický zápis výpočtu kovariance je uveden ve vzorci (3). Vypadá možná složitě, ale přesně popisuje, jak se k výpočtu doberu. Bude to konkrétně pro mé dvě nevelké datové řady znamenat, že každou z dvojice datových bodů odečtu od svých průměrů (zjistím vzdálenost ke své střední hodnotě pro svou datovou řadu) a zjištěné vzdálenosti mezi sebou vynásobím, takto to provedu pro každou z osmi dvojic dat. Všech osm součinů (jejich výsledky) sečtu a vydělím celkovým počtem provedených součinů, tedy zjistím aritmetický průměr těchto velikostí součinů jednotlivých vzdáleností od středních hodnot. To je celé, výsledek mi představuje hodnotu kovariance pro analyzovaný vztah mezi akciemi A a B. Konkrétně pro ilustraci na obrázku níže.
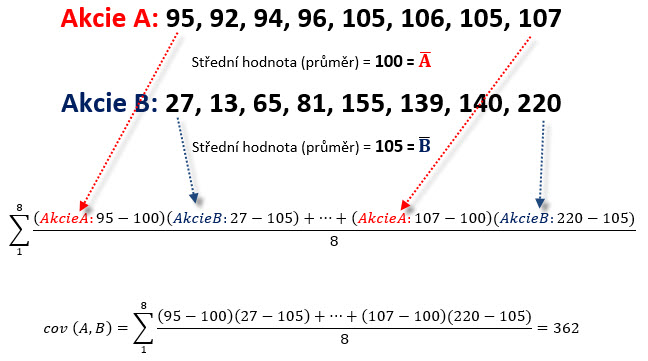
Postupné sečítání součinů vzdáleností ke svým středním hodnotám je znázorněno šipkami pro první a nakonec poslední dvojici dat. Není to nic složitého, jsou využity pouze základní početní operace, výsledkem je pak hodnota +362. Provedeným výpočtem pak mohu konstatovat, že kovariance akcií A,B je kladná a má hodnotu právě +362. Co je to za číslo? Těžko jej lze nějak prakticky interpretovat, když představuje průměr součinů vzdáleností vzájemných dvojic dat od svých středních hodnot, takže stěží mohu hovořit o průměrné velikosti čtverce jako v případě rozptylu, v tomto případě představuje kovariance opět jakési dvojrozměrné číslo charakterizující průměrné „spolurozptýlení“ analyzovaných datových řad. Tato interpretace však není nyní nutná, postačí mi základní povědomí, co by mohla hodnota kovariance na úrovni +362 znamenat. Na obrázku je část výpočtu modelového příkladu.
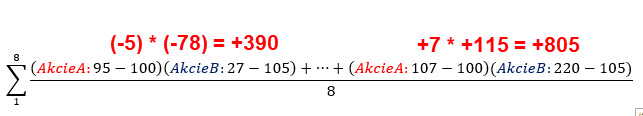
Mohu pozorovat, že první součin (95-100)*(27-105) přinesl součin záporných čísel, který je ve výsledku kladným číslem. Znamenalo to, že obě záporná čísla tvořící součin (ceny akcií obou datových řad pro první pozorování) se nacházela pod střední hodnotou svých datových řad (cena 95 pod průměrem s hodnotou 100 pro akcii A a cena 27 pod průměrem hodnotou 105 pro akcii B). Stejně mohu pozorovat, že poslední součin (107-100)*(220-105) přinesl součin kladných čísel, který je ve výsledku opět kladným číslem. Znamenalo to, že obě kladná čísla tvořící součin (ceny akcií obou datových řad pro poslední pozorování) se nacházela nad střední hodnotou svých datových řad (cena 107 nad průměrem s hodnotou 100 pro akcii A a cena 220 nad průměrem s hodnotou 105 pro akcii B). Součin obou kladných čísel přispěl ke kladnému výsledku celé hodnoty kovariance. Nacházení se dvojice dat k součinu současně buď nad svými průměry nebo obě současně pod svými průměry způsobuje kladný příspěvek k celkové kovarianci a znamená, že pokud se současně obě počítaná data nacházejí ve stejné poloze nad svými průměry nebo pod svými průměry, je to známka jakési vzájemné vazby mezi takto zjištěnými daty, obě se tedy nacházejí na správné straně vzhledem ke svým středním hodnotám. Mohu tak předpokládat, že obě datové řady s kladnou hodnotou kovariance budou mít tendenci se chovat podobně, tedy současně růst nebo současně klesat, protože to bude znamenat, že se budou nacházet na stejné straně vzhledem ke svým středním hodnotám, pohne-li se cena k následnému měření a následný součin další dvojice dat se bude nacházet opět na stejné straně vzhledem ke své střední hodnotě a vygeneruje další kladný součin, přispěje tento ke „kladnosti“ celého výsledku vypočítané kovariance. Na obrázku níže jsou vyobrazeny obě datové časové řady s výslednou kladnou kovariancí, která charakterizuje vztah mezi oběma datovými řadami.
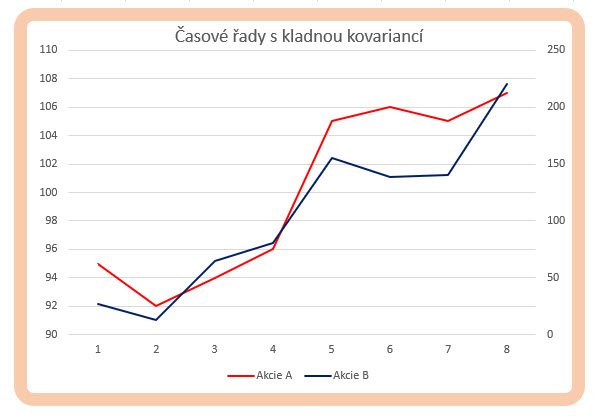
Je patrné, že pohyb obou datových řad má určitou pozorovatelnou závislost, obě řady přibližně současně klesají nebo společně rostou.
Co by způsobilo, aby se celková hodnota kovariance měla tendenci tlačit pod hodnotu nula do záporných hodnot? Takový výpočet by musel znamenat, že obsahuje součiny, které jsou ve výsledku záporné a bude jich v absolutní hodnotě součtů více než těch kladných, záporný součin pak vygenerují taková data, která pro jednotlivé dvojice vykazují opačnou polohu ke své střední hodnotě, tedy pokud se cena akcie A nachází nad svou střední hodnotou a současně se cena akcie B nachází pod svou střední hodnotou (nebo naopak), bude součin těchto vzdáleností nakonec záporný a bude způsobovat, že bude stlačovat výsledek kovariance do záporných hodnot. Současná poloha sledovaných dvojic dat s opačnou polohou vůči své střední hodnotě pak ve zjednodušené interpretaci znamená, že obě datové řady s vypočítanou zápornou hodnotou kovariance budou mít tendenci se chovat zcela opačně, tedy při růstu jedné datové řady bude druhá datová řada klesat. Na obrázku níže je velmi jednoduchá úprava modelových dvou časových řad.

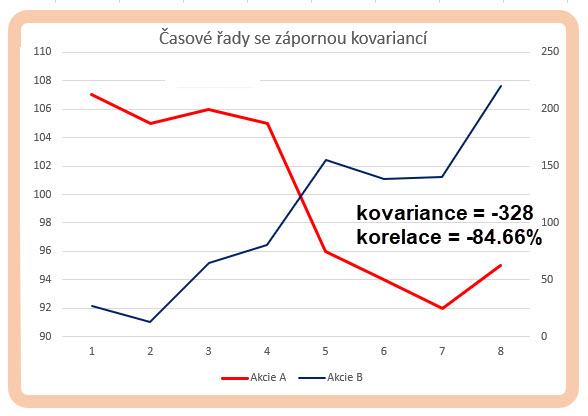
Ceny akcií A jsem přepsal do obráceného pořadí, samozřejmě, že průměry (střední hodnoty) zůstávají stejné. Pokud bych nyní provedl součin prvních dvou hodnot vzdáleností ke svým středním hodnotám v obou datových řadách (107-100)*(27-105) = +7*(-78) = -546, vyjde tato záporná hodnota, protože cena akcie A se v této chvíli nachází nad střední hodnotou, kdežto cena akcie B se nachází pod střední hodnotou. Celkově je kovariance obou datových řad na záporné hodnotě -328. Co tato záporná hodnota představuje je patrné z obrázku níže.
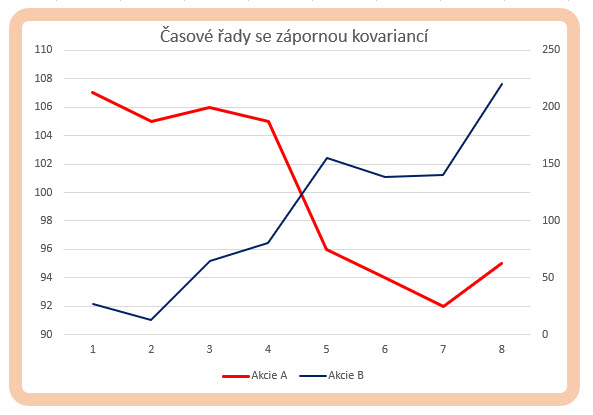
Je patrné, že záporná hodnota kovariance popisuje opačné chování cen obou datových řad, za současného růstu jedné datové řady druhá datová řada klesá a naopak.
Zjišťování hodnoty kovariance časových řad pomocí Excelu obstarává funkce =COVARIANCE.P se zadáním obou oblastí porovnávaných časových datových řad, zjištění vypočítané hodnoty na rozsáhlých datových souborech je tak otázka okamžiku
Zjišťování kovariance, tedy zjištění míry závislosti obou časových datových řad nemusí nutně ustrnout na výpočtu pro dvě datové řady, je možné zjišťovat víceřadé závislosti sestavováním a řešením kovariančních matic, to je však mimo dimenze tohoto článku.
Korelace (Correlation)
Zjistit, jaká je kovariance datových řad s výsledkem nějakého čísla udávajícího průměr součinů vzdáleností jednotlivých odpovídající datových údajů od svých středních hodnot je pro představivost a interpretaci stejně nepohodlné, jako údaj o rozptylu z analýzy datového souboru, který představuje průměrný čtverec vzdálenosti od své střední hodnoty. Odebrat údaji o zjištěné kovarianci charakter průměrného součinu, nějakým způsobem tento údaj standardizovat a umět jej jednoduše vysvětlit je úkon připomínající odmocnění hodnoty rozptylu ke získání hodnoty standardní odchylky. Tímto úkonem pak v případě kovariance bude převést vypočítanou kovarianci na jednorozměrné číslo, a to za použití právě již známých hodnot směrodatné odchylky pro obě porovnávané datové řady. Mohu tak pro modelový příklad využít opět mé časové datové řady a pouze využít již vypočítaných hodnot.

Datové řady představující například osm po sobě jdoucích měsíčních zavíracích cen akci A a akcií B mohou mít střední hodnoty na úrovni 100 (akcie A) a 105 (akcie B). Standardní odchylka, tedy průměrná vzdálenost datového údaje každé z datových řad je vypočítána (například pedantských dosazením do vzorce, odmocněním rozptylu nebo pomocí Excelu) na hodnotu 5.87 pro řadu akcií A resp. 65.98 pro řadu reprezentující akcie B. Jakým způsobem tedy mohu standardizovat hodnotu kovariance na užitečné číslo? Pokud kovariance představuje průměrný součin vzdáleností jednotlivých datových bodů ke svým středním hodnotám, pak se bude jistě jednat o „nějakou plochu“ (například obdélníku). Pokud mezi sebou vynásobím hodnoty standardních odchylek, tedy průměrné vzdálenosti datových bodů pro každou z datových řad, vypočítám také „nějakou plochu“ (pravděpodobně opět nějakého obdélníku), tento ale bude představovat jakousi průměrnou plochu pro obě datové řady. Pokud poté mezi sebou porovnám plochu zjištěnou kovariancí a průměrnou plochu zjištěnou standardními odchylkami, mohu vypočítané číslo lépe pochopit, protože se bude jednat o číslo, které se bude pohybovat v intervalu od -1 do +1. Přesně tímto způsobem vypočítám koeficient korelace, tedy korelaci mezi oběma datovými řadami. Obecně tedy mohu toto porovnání ploch, jako postup pro výpočet korelace, popsat takto:
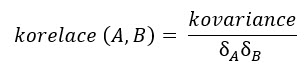
Dosazením do vzorce pro analyzované modelové datové řady s kovariancí +362 a se standardními odchylkami 5.87 a 65.98 se pak mohu dopočítat k následujícímu výsledku:
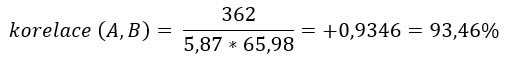
Protože jsem upravoval kladnou kovarianci (+362) mých modelových datových řad, která popisuje vztah současného růstu hodnoty prvků jedné datové řady růstem prvků druhé datové řady, součinem standardních odchylek, je patrné, že výsledek bude také kladný a ukáže mi míru takového vzájemného vztahu vyjádřenou jediným srozumitelným číslem. Protože se hodnota korelace pohybuje mezi hodnotami -1 a +1, mohu ji také vyjádřit procenty, ukazujícími na míru vzájemné závislosti také z tohoto procentního pohledu. Kladná hodnota vypočítaného korelačního koeficientu +93.47% mi ukazuje, že tato korelační závislost obou časových řad je velmi významná a znamená, že pohyb ceny akcie vzhůru bude také znamenat výrazně vysokou pravděpodobnost, že také cena druhého akciového titulu bude narůstat. Grafické shrnutí na obrázku níže.
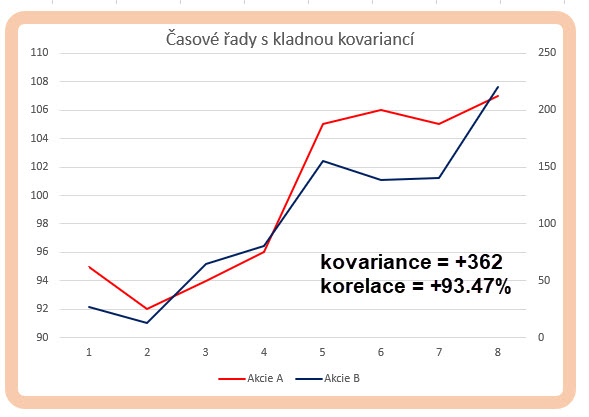
Pohyb vypočítané korelace v intervalu (-1;+1) znamená, že pokud bude hodnota korelačního koeficientu klesat z vypočítaných kladných hodnot k nule, bude se také vytrácet významnost vztahu mezi oběma datovými řadami, když výpočet korelace s hodnotou nula bude znamenat, že vztah mezi porovnávanými datovými řadami není žádný. Korelační koeficient se zápornou hodnotou pak bude naznačovat opačné chování prvků analyzovaných datových řad, zejména proto, že ke standardizaci kovariance vycházíme při dosazení do vzorce výpočtu korelace z její záporné hodnoty. Záporná korelace pak bude znamenat, že pokud se hodnota prvků v jedné datové řadě zvyšuje, hodnota prvků v druhé časové řadě se snižuje. Grafické shrnutí s vypočítanou zápornou kovarianci a zápornou korelací na obrázku níže.
Korelace tak měří míru lineární závislosti obou zkoumaných časových datových řad, kvantifikuje, nakolik se při změně hodnoty datového bodu změní hodnota bodu druhé časové řady. Je důležité vědět, že linearita závislosti vychází ze způsobu výpočtu korelace, tedy pokud bych mohl předpokládat, že koeficient korelace bude +1.00 (+100%), bude to znamenat, že například změna ceny akcie A o +4% bude znamenat také dokonale podobnou změnu ceny akcie B o +4%. Pokud bych si každou takovou změnu ceny, která bude pro obě datové řady v takto dokonalém souladu, vynesl do grafu s osami představujícími akcie A a akcie B, výsledným útvarem by byla přímka. Na obrázku níže jsou dvě dokonale korelované časové řady, mohou tak opět představovat například ceny dvou akciových titulů měřené ve stejných časových okamžicích.

Korelační koeficient je +1.00 a znamená +100% korelaci obou akciových titulů. Pokud bych si vynesl jednotlivé prvky datových řad do bodového grafu, mohu pozorovat tento průběh.
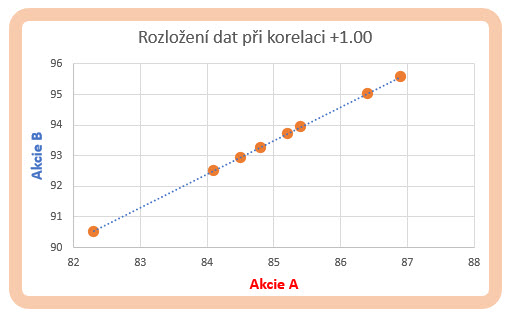
Jednotlivé body cenových průběhů obou akciových titulů bych mohl proložit ideální přímkou, dokonalá závislost má tedy dokonale lineární průběh, sklon křivky stoupající zleva doprava znamená, že stoupání hodnoty akcie A bude doprovázeno také zvyšováním ceny akcie B a naopak. Každá nedokonalost narušující takto ideální korelaci bude znamenat níže zobrazený výskyt takto zobrazeného bodu nesplňujícího 100% korelaci mimo ideální přímku.
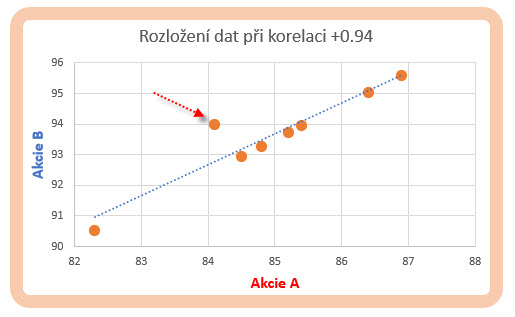
Dokonale korelované datové řady narušil výskyt jedné dvojice datových bodů nesplňující dokonalou linearitu vzájemných vztahů a snížil koeficient korelace na +94%. Souřadnice takové dvojice vynesly umístění výsledku mimo ideální spojnici trendu – přímku stoprocentní (ideální) korelace.
Mohu také pro úplnost prozkoumat časovou datovou řadu s korelací zápornou na mezní hodnotě -1.00, tedy -100%. Takto korelované časové řady se vyznačují dokonalou opačnou vzájemnou závislostí jednotlivých „datových dvojic“, růst hodnot jedné datové řady je doprovázen dokonale proporcionálním poklesem hodnot druhé časové řady. Mohu se pak pokusit graficky zobrazit takto dokonale opačně korelované datové řady ve stejném grafu souřadnic a pokusit se nalézt spojnici těchto bodů a předpokládat, že budou opět tvořit přímku.
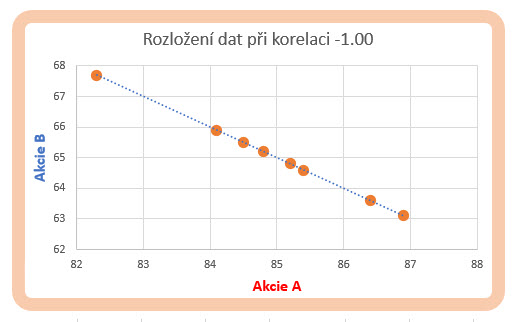
Tento předpoklad, že spojnice takto zobrazených bodů bude lineární se opravdu potvrdil, mohu ale nyní pozorovat opačný sklon této přímky, který je ve znamení poklesu ve směru růstu ceny akcie A (osa x), potvrzuje to tak vypočítanou zápornou hodnotu koeficientu korelace, tedy růst hodnoty jedné časové řady je doprovázen poklesem hodnot druhé časové řadu, v tomto případě v dokonalých proporcích.
Absence jakékoliv vazby mezi cenovými řadami je naznačena vypočítanou hodnotou koeficientu korelace na hodnotě 0.00. Časové datové řady s takto zjištěným koeficientem mohu pro úplnost dokresli grafickým znázorněním na obrázku níže.
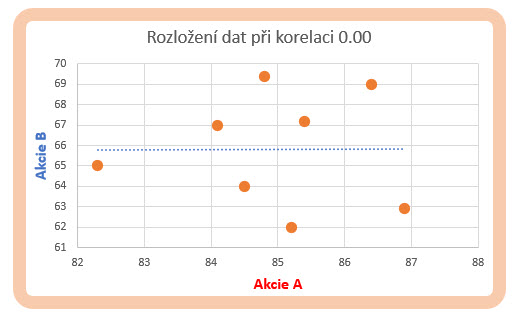
Absence sklonu ideální spojnice všech datových bodů reprezentující jednotlivé cenové údaje obou analyzovaných datových řad a výskyt neprosto neuspořádaného rozložení jednotlivých bodů po celé ploše grafu nepřimykajícího se k nějaké pozorovatelné přímce je charakteristické právě pro takto nekorelované datové řady.
Výpočet a analýza korelace je hledání a kvantifikování lineární závislosti obou časových řad, protože se pokouším právě o hledání závislosti ve vztahu k takto namodelované přímce. Ve skutečnosti však může být závislost mezi datovými řadami nikoliv lineární, ale například může jednotlivým datovým bodům odpovídat jiná a ideálnější spojnice, mohou mít například blíže k nějakému tvaru exponenciální nebo logaritmické křivky, na kvantifikaci takového vztahu mezi jednotlivými datovými řadami však nemohu použít výše uvedený výpočetní postup pro stanovení korelačního koeficientu, ale jiné a sofistikovanější matematické a statistické postupy. Koeficient korelace mohu samozřejmě zjistit také pomocí Excelu, kde zabudovaná funkce =CORREL s označením oblastí vyhodnocovaných datových řad dokáže vypočítat hodnotu tohoto koeficientu bez znalosti jakéhokoliv výpočetního postupu.
Komentáře a příspěvky k tomuto článku prosím směrujte do Diskuzního fóra do tohoto vlákna :c)
Sleduj facebook, napiš e-mail nebo tweet