
V minulém článku Cena opce jsem se pokusil popsat, jak je možné si alespoň zjednodušeně představit zcela zevrubnou stavbu stanovení ceny opčního kontraktu. Protože mám rád převod teoretických úvah do praktického obchodování (vlastně o nic jiného mi ani nejde), tak bych se v intencích těchto lehce éterických myšlenek pokusil tuto úvahu o stanovení ceny opčního kontrakt zasadit do nějakého smysluplného rámce. Jednoduše chci, aby mi taková znalost určení alespoň ceny opce dávala nějaký smysl pro nějaká další obchodní rozhodnutí. V minulém článku jsem také ukázal velmi jednoduchý Excel s naprogramovaným i funkcemi cen opcí Call a Put pro okamžité zjištění ceny opčních kontraktů, které využívá Black-Scholesův oceňovací model.
Pokud bych si tedy alespoň v základech osvojil schopnosti určit si podle nějakého modelu teoretickou cenu opčního kontraktu, například podle vlastního Excelu nebo pomocí nějaké aplikace, bylo by pak otázkou, k čemu mi taková vypočítaná a teoretická hodnota ceny opce vlastně je? Odpověď je jednoduchá. Byl bych si totiž schopen velmi jednoduše odpovědět na kardinální obchodní otázku „…je to, co kupuji drahé nebo levné ?…“
Abych byl schopen na tuto otázku nějak férově odpovědět v praktickém životě, tak při zjišťování, jestli je kilo česneku v našem Albertu drahé nebo levné mi bude stačit jednoduše odskočit do Lidlu a Billy a zjistit, kolik stojí tam a podle toho padne mé jednoduché konečné nákupní rozhodnutí. Pokud ale kupuji něco, co nikde jinde neprodávají, protože se jedná například o unikátní druh zboží, které jinde prostě nemají, musím se vydat jinou cestou srovnání. Nejjednodušším srovnáním by pak mohlo být zjišťování, jestli v tomto obchodě cena takového unikátního zboží byla v historii vyšší nebo nižší a z takového zjištění pak vytvořit mé vlastní obchodní rozhodnutí ve vztahu k dnešní nabízené ceně. Protože pořizování opčních pozic je zcela unikátní a originální záležitost, vyjdeme prostě z tohoto jednoduchého srovnávacího přístupu. Přestože vím, že existují sofistikované modelovací opční aplikace, přece jenom si myslím, že by nebylo špatné pochopit, jak by takové historické srovnání mohlo fungovat a co by mohlo být jeho podstatou.
V minulém článku s přiloženým Excelem jsem ukázal, jak hodnota Implied Volatility velmi podstatně ovlivňuje hodnotu opčního kontraktu v reálném čase. Pokud budu mít k dispozici údaje o Ceně Podkladu, Strike, Délce života opce, Implied Volatilitě, Úroku a Dividendě, tak jsem schopen si cenu opce spočítat. Tak bych jednoduše zjistil, kolik opční kontrakt stojí nyní na trhu, za kolik se takové „zboží“ aktuálně nabízí. K tomu ale nepotřebuji žádné analytické aplikace nebo vlastní excelovské výpočty, to mi opravdu stačí se podívat do opční platformy a nemusím o takových výpočtech aktuální ceny vůbec přemýšlet. Problém je v tom, že pokud se podíváte do různých opční platforem různých brokerů, uvidíte téměř totožné „aktuální ceny zboží“ – opčních kontraktů, takže takovými pohledy vlastně nic o ceně nezjistíte. Jaká by však hodnota zboží měla skutečně být, by mělo vyplynout ze srovnání této skutečné ceny s cenami, které byly vytvořeny pro dané zboží – opční kontrakty – v minulosti. Pro jednoduché srovnání proto budu vycházet nikoliv z hodnoty Implied Volatility, tedy volatility, která je u daného opčního kontraktu „Implied“ (očekávána), ale z hodnoty Historické Volatility, kterou zakomponuji do opčního modelu, abych zjistil toto historické srovnání. Takže vlastně porovnávám, jaká by hodnota opce měla být ve vztahu k minulým hodnotám na základě volatility podkladu, který se odehrával v nejbližší minulosti s hodnotou, kterou skutečně vidím v opčním řetězci a je mi reálně nabízena.
Historická volatilita je hodnota, která v matematickém vyjádření představuje skutečné pohyby podkladového aktiva, tak, jak se udály v minulosti. Někdy je možné se také setkat s označením Realizovaná Volatilita, oba pojmy však pojmenovávají to nejpodstatnější, a to skutečnost, že se jedna o hodnotu odrážející již proběhlou historickou volatilitu, tedy takovou, která se opravdu skutečně stala a na trzích příslušného podkladu realizovala. Můžu si ji také velmi jednoduše spočítat pomocí funkcí v Excelu. Abych mohl celý výpočet provést, měl bych její výpočet pochopit. Přestože se mě její hodnota ukazuje ve všech obchodních platformách, je celkem neuvěřitelné, jak se její hodnoty liší, protože při jejím výpočtu mohou být zvoleny určité odlišné postupy. Pokud bych vyšel z nějaké ustálené definice, tak Historická Volatilita vyjadřuje standardní odchylku mezidenního pohybu podkladového aktiva za sledované období převedenou do anualizovaného tvaru. Protože to zní velmi nepřehledně, tak celou situaci ukáži v praxi na jednoduchém příkladu akcie Facebook (FB), kde budu chtít zjistit nejrozšířeněji využívanou hodnotu 30-ti denní Historické Volatility.
Na obrázku je vidět rozdělenou definici výpočtu HV do třech kroků, jak byla postupně spočtena.
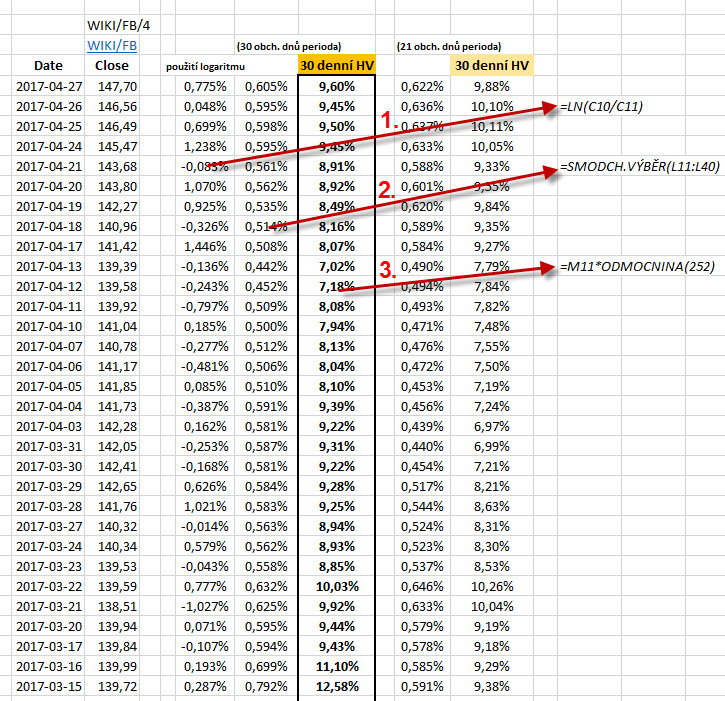
Bod 1. Výpočet mezidenního pohybu. K tomuto výpočtu byly použity hodnoty Close na akcii FB, tak je možné je bleskově to excelu načíst například z Quandl.com. Je s podivem, jak mnohé aplikace vypočítávají mezidenní pohyb jako rozdíl mezi Close hodnotou dnes a včerejší. Na obrázku je uveden výpočet pomocí přirozeného logaritmu podílu těchto cen. Proč? Z jednoduchého důvodu, pokud bude mít dnes FB hodnotu 100 USD a jeho cena se zvedne o 10%, tak bude mít zítra hodnotu 110 USD, pokud ale pozítří cena opět klesne o 10% zpět, tak výsledná hodnota FB bude 99 USD, nikoliv původních 100 USD, proto tento logaritmický výpočet, který takový početní nesoulad vyhlazuje. Některé aplikace také nepracují jen s rozdílem těchto Close cen, ale porovnávají například High a Low jednotlivých dnů, aby bylo přesněji zachyceno, co všechno taková akcie může v těchto srovnávaných dnech „předvést“ za pohyby, toto může být také zdrojem výrazných zkreslení.
Bod 2. Výpočet standardní odchylky za sledované období. K tomuto výpočtu využijeme funkci v excelu, to není žádný problém, problémem může být, jaký rozsah období do tohoto výpočtu zahrneme. Pokud hledám hodnotu 30-ti denní Historické Volatility, tak musím vědět, že pokud zahrnu do výpočtu 30 hodnot (jako na obrázku) vypočtu tuto Historickou Volatilitu za posledních 30 obchodních dnů, nikoliv poslední měsíc, toto bych dosáhl, pokud bych do výběru zahrnul pouze posledních 21 hodnot – dnů (průměrný počet obchodních dnů v měsíci). Na pravé straně obrázku v posledním sloupci vidíte rozdíl mezi hodnotami, pokud je 30-ti denní HV spočtena právě jen z období posledních 21 dnů – rozdíly jsou patrné a mohou se lišit o jednotky procent (pak by se asi mělo mluvit o „měsíční Historické Volatilitě“). Volba délky takového období tedy také může způsobit výrazná zkreslení ve výpočtu. Pokud bychom chtěli vytvářet jiné periody Historické Volatility (například 100 dnů, jeden rok…), tak k tomu nám postačí pouze upravit rozsah takové excelovské periody.
Bod.3. Převod do anualizovaného tvaru. Pokud spočítáme hodnotu směrodatné odchylky, musíme ji převést do tvaru, který vyjadřuje její roční hodnotu – „anualizaci“, toto provedeme jednoduše tak, že hodnotu této odchylky vynásobíme druhou odmocninou hodnoty 252, která představuje průměrný počet obchodních dnů v roce. Rovněž musím upozornit, že některé modely mohu používat hodnotu druhé odmocniny z čísla 365.
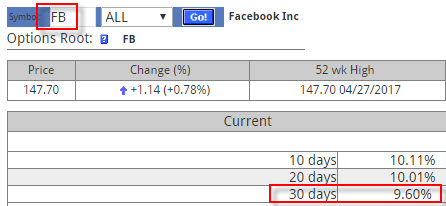
Pokud tedy použiji výpočet mezidenních rozdílů pomocí přirozeného logaritmu, použiji 30 dnů, jako periodu výpočtu standardní odchylky a anualizaci vyřeším odmocninou z čísla 252, tak hodnota 30-ti denní Historické Volatility u akcie FB je k tomuto okamžiku na hodnotě 9,60%, tedy úplně stejná hodnota, jak je prezentována například na stránkách iVolatility.com. Toto vše můžete vidět na přiloženém obrázku.
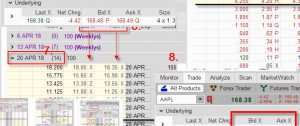
Pokud tedy tuto hodnotu Historické Volatility využiji k mému srovnání a vyhodnocení, jak na tom jsem s cenami opcí na FB nyní, mohu k tomu použít například Excel s předchozího příspěvku, který vypočítával teoretickou cenu opcí (na druhém listu tohoto Excelu je výpočet Historické Volatility podle předchozích odstavců). Budu se tedy zabývat otázkou, jaké jsou ceny například ATM opcí na strike 150, které bych chtěl dnes pořídit s expirací za 21 dnů, tedy expirace klasické měsíční opce. Do Excelu vložím zadané hodnoty momentální ceny podkladu, data pořízení a expirace, strike a případně úrokové míry, za volatilitu dosadíme hodnotu 9,60%, tedy hodnotu Historické Volatility, která reprezentuje volatilitu podkladu za uplynulých 30-ti dnů a budu sledovat, jaké jsou projekce ceny opce podle této Historické Volatility a srovnám je z aktuálně nabízenými cenami.
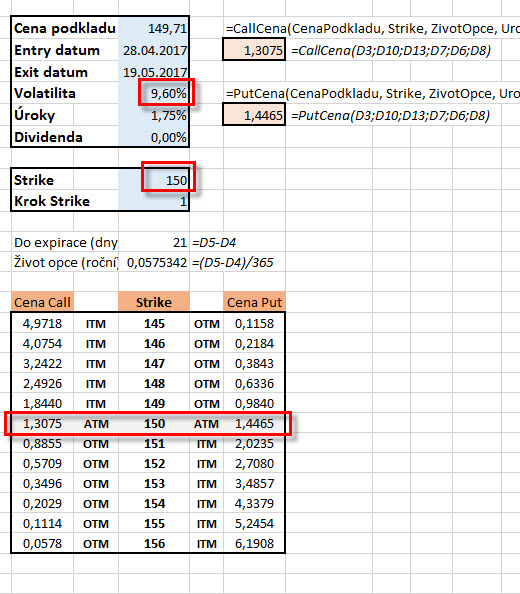
Podle mého jednoduchého výpočtu na základě hodnoty předcházejících pohybů akcie FB, kterou mi reprezentuje 30-ti denní Historická Volatilita ve výši 9,60% by pak měly být ceny Call opcí na hodnotě 1,31 a Put opcí na hodnotě 1,45. Na níže uvedeném obrázku je vidět aktuální cena opcí, za kterou je na sledovaném strike 150 můžeme ve skutečnosti pořídit.
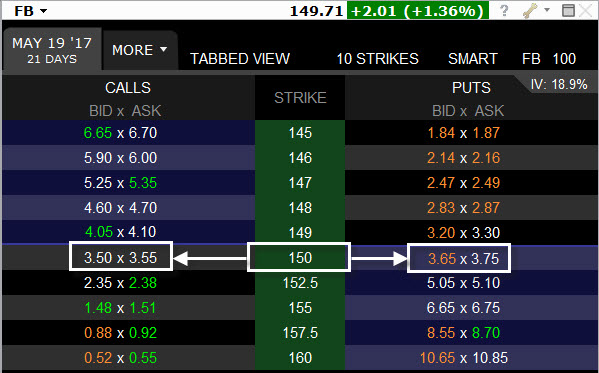
Výsledek takového srovnání je velmi výrazně odlišný, podle Historické Volatility a minulých pohybů na akcii FB, by měla Call 150 stát 131 USD a Put 150 by měla stát 145 USD. Místo toho však Call 150 stojí 350 USD a Put 150 má aktuální cenu 375 USD, tedy Call je nabízena za cenu o 219 USD vyšší a Put za cenu o 230 USD vyšší, než by se na základě minulého vývoje čekalo, aktuální ceny jsou tak dražší více než o 100% !!! Co z toho plyne? Opce jsou velmi drahé. Znamená to, že akcie FB si prošly v posledním období velmi klidným a nevolatilním vývojem, které způsobilo, že Historická Volatilita je na velmi nízké úrovni pod 10%, tento minulý vývoj ale není vůbec přenesen do aktuálních tržních cen, mám ve výpočtu chybu?
Pokud bych chtěl ze současných, velmi vysokých cen vysledovat, jaká je současná Implied Volatilita, která byla použita k výpočtu současných cen opcí na strike 150, tak bych pomocí aplikace na Livevol mohl vypočítat, že její hodnota je 25,43%, tedy úplně někde jinde, než je má „excelovská“ hodnota 9,60%.
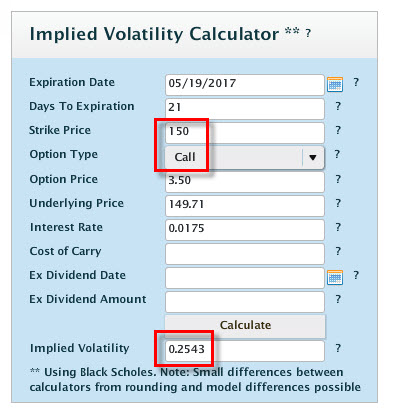
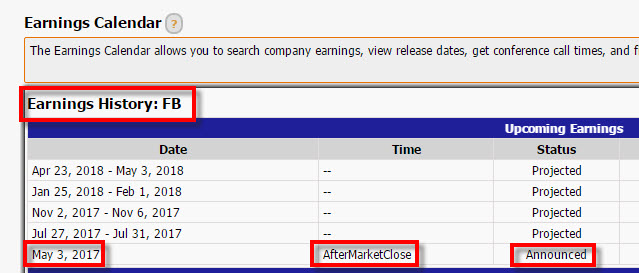
Proč tomu tak je? Vysoká Implied Volatilita, více než dvojnásobná oproti volatilitě Realizované a Historické znamená, že v období do expirace opčního kontraktu, kterým se ve výpočtu zabývám, je promítnuta nějaká očekávaná událost, která způsobuje tak dramatický růst ceny opčního kontraktu. Takovou událostí je očekávané vyhlašování hospodářských výsledků za první kvartál ohlášené na 3.května 2017 po uzavření trhů. Tato událost se stane za života mé sledované opce a signalizuje, že podkladová akcie může v souvislostí s touto událostí udělat nějaký mimořádný cenový pohyb a tento pohyb je promítnut do hodnoty Implied Volatility a samozřejmě do ceny opčních kontraktů. Informace o projekci termínů vyhlašování hospodářských výsledků můžete v ucelené podobě zdarma najít například na Marketchameleon.com.
Pozorování vývoje obou volatilit – Historické a Implikované – je základem a předmětem mnoha obchodních opčních strategií, které budu v budoucích článcích popisovat. Odpověď na otázku, jestli je opce nyní drahá nebo naopak levná je jedním se základních předpokladů k rozhodnutí, jak vstupovat do různých opčních pozic, zejména jaké opce k tomuto využít. K velmi rychlé a jednoduché vizualizaci a vyhodnocení takového fenoménu diskrepance mezi volatilitami mohou být například grafy takových Volatilit, které můžu zdarma získat na stránkách iVolatility.com
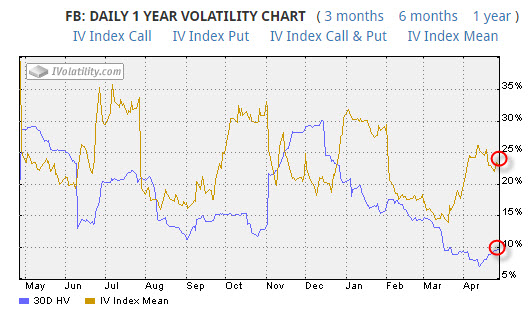
Na obrázku je vidět grafické znázornění průběhu 30-ti denní Historické Volatility (modrá křivka) za současného zobrazení průběhu Implied Volatility (hnědá křivka) u akcie FB. Takové křivky pak reprezentují v obecném pohledu naděje a očekávání do akcie vkládané (křivka IV), ve srovnání se skutečným a reálným naplňováním takových nadějí a očekávání (křivka HV). Zcela zřetelně je vidět, že předpoklady a realita jsou dvě diametrálně odlišné věci, takový ale obecně není jen cenový vývoj akcie Facebook, ale život sám :c)
Sleduj facebook, napiš e-mail nebo tweet
Moc pěkné články.
Osobně si myslím, že používat zrovna 30 denní volatilitu je podivná zvyklost a moc jí nerozumím. Asi je to způsobené tím, že si to tvůrci platforem a snad i obchodníci chtějí zjednodušit.
Proč zrovna třicet dní a ne třeba 60? Nebo rovnou 365? S kolegy jsme si nedávno vytvořili jakousi svojí vlastní „exponenciální volatilitu“ , která počítá s delším obdobím, ale poslední pohyby mají větší váhu než pohyby minulé. Do toho se ale motá to, že některé extrémní pohyby je třeba z výpočtů vynechat, protože byly jednorázové a neodpovídají běžné volatilite podkladu. Dají se s tím dělat všelijaké hrátky 🙂 To se mě osobně na opcich líbí, ta rozmanitost. Ať se daří.
Ahoj Pavle, máš pravdu v tom, že ta variabilita při obchodování opcí je neskutečně široká. Člověk si to ale může výrazně zkomplikovat právě nějakými hlubšími ponory, aby nakonec zjistil, že mu unikne pravá podstata problému. Protože je pochopení volatility při obchodování opcí základní věc, tak také souhlasím, že právě zkoumání různých volatilit na jiných délkách časových period může leccos napovědět, co zůstává na první pohled skryto. Na obrázku Volatility NFLX je například vidět různé průběhy jednotlivých volatilit na akcii NFLX. Volatility s dlouhodobější periodou nemají takové razantní dna a vrcholy jako 30-ti denní, tak asi proto je tato nejběžněji používaná, ale to si opravdu každý může vyrobit podle svého. Já jsem chtěl v tomto článku ukázat, že je možné si to jednoduše vypočítat „doma“ a sám si pak kdokoliv může zvolit jakoukoliv periodu. Díky a přeji „dobré trejdy“, Jirka
Dobrý den,
děkuji za parádní články. Rád bych se zeptal, když jsem zkoušel hledal poslední graf v článku na iVolatility.com tak jsem našel pouze program který mi to ukáže , ale je zdarma pouze první měsíc. Špatně hledám nebo je to již zpoplatněno?
Děkuji a ať se daří
Ahoj, stačí si na iVolatility vytvořit zdarma základní registraci a poté z hlavní stránky kliknout na jeden z grafů (BMY nebo KORS). Tak se dostaneš na stránku ze základními údaji o volatilitě, kde můžeš zadávat do pole „symbol“ požadované tituly. V pravém dolním rohu vedle tabulek s údaji jsou vždy požadované grafy, které kliknutím zobrazíš, mě to funguje již několik let a nic nikomu neplatím, ahoj, Jirka :c)
Ahoj Jiří, také díky za pěkné čtení. Pro začátečníka je to úplně super a začínám se díky tvým článkům již trochu orientovat ve světě opčních obchodů. Chci se zeptat, není stejné porovnání implied a historické volatility jako na iVolatility.com také v aplikaci TOS?
Měj se pěkně, Lukáš
Ahoj Lukáši,
kupodivu není, protože IV vypočítávaná na iVolatility.com a TOS je pokaždé jiným způsobem. IVolatility zobrazují IV Index, tedy jakési číslo, které se vypočítává jako vážený průměr volatilit na ATM strike podle „nějakého jejich výpočtu“, kdežto TOS má něco obdobného, ale algoritmus výpočtu je jiný „jejich vlastní“. Čísla se pak neshodují i když jsou si velmi podobná a pro základní práci úplně postačí, jenom dodávám, že Interactive Brokers má tyto hodnoty také jiné, takže si potom vyber, není třeba si ale kvůli tomu lámat hlavu, protože ty rozdíly jsou pro nějaké zásadní obchodní rozhodnutí nepodstatné, protože do začátku stačí, jestli je IV vysoká nebo nízká nebo alespoň poznání, že „nějak vybočuje z normálu“, ahoj, Jirka :c)
Ahoj Jirko,
čistě základní (a možná stupidní dotaz) – HV a IV porovnáváš proto, abys došel k tomu, zda je cena opce u brokera podle toho porovnání levná či drahá. Není už sama tahle myšlenka nesprávná? Budoucí vývoj trhu přece nelze usuzovat z historického vývoje. Historický vývoj sice něco málo napoví, ale neměl bych se podle něj stavět své rozhodování. Navíc, do vzorců pro výpočet IV mohou vstupovat další faktory (zmínil jsi earnings date, ale může to být v podstatě cokoliv, co ovlivňuje cenu podkladového aktiva).
Jak si se vypořádal s tímto základním problémem? Předpokládám, že sis nějak ověřil, že metoda srovnání IV a HV se jako faktor pro rozhodování hodí, jen by mě to zajímalo.
Moc díky za odpověď i za Tvou práci na tomhle skvělém webu.
Josef
Ahoj Josefe,
pokud cena opčního kontraktu vychází z pevně daných hodnot (v určitému okamžiku) – ceny podkladu, hodnoty strike, doby do expirace, úroků a existenci vyplácené dividendy do expirace a pouze z jediné neznámé – Implied Volatility, pak tato IV bude základním cenotvorným prvkem opčního kontraktu. Máš pravdu, že to, co se stalo v minulosti nutně nemusí platit pro budoucnost, ale co jednoduššího mi zbývá, než porovnat historické úrovně volatility s aktuálně vloženou volatilitou do ceny opčního kontraktu? Existují značně sofistikované modely, které se snaží stanovit hodnotu IV tak, aby odrážela co nejvěrněji očekávání budoucího cenového vývoje podkladu, ale pořád to jsou jen modely, výpočty a odhady s nějakou mírou pravděpodobnosti, které se nakonec nemusí vyplnit. Cena opcí stoupá při očekávaných budoucích událostech právě proto, že se zvyšuje pravděpodobnost pohybu podkladu (Earnings…), tedy očekávaná volatilita a mohu se podívat do historie, jakých úrovní dosáhla v minulosti a předpokládat, že podobných úrovní dosáhne i před nynějším Earnings, což se ale nakonec nemusí identicky vyplnit….Srovnání HV a IV používám v nejběžnější formě tak, že pokud chci nakoupit opční kontrakt co nejlevněji, tak se podívám na graf IV a pokud je v nějakém významném spike nebo obecně na vysoké úrovni, tak je to pro mě signál, že kupuji za vysokou cenu a mohu tratit již jen z této skutečnosti, tedy z nevhodné doby pro nákup. Je totiž pro mě nemožné vyhodnotit pouhým pohledem na opční řetězec, že pokud kupuji Long Call JNJ na strike 170 s expirací za dva měsíce za cenu 200 USD, jestli kupuji draze nebo levně. Mohu ale s pohledu na graf IV vypozorovat, že se nachází na neobvykle nízkých úrovních v porovnání z minulostí a tedy mohu být klidný, že nenakupuji předražený opční kontrakt…Jirka :c)