Obchodování mého osobního traderského účtu nevyžaduje nijak významné nároky na kontrolu rizika, se kterým na tomto účtu pracuji. Mám přesně danou skladbu svých pozic, vím dopředu, kolik mohu maximálně ztratit a na požádání pravděpodobně vyjmenuji kompletně všechny jednotlivé pozice mého portfolia. Povědomí o celkovém přijatém riziku mého malého účtu mám pod detailní kontrolou pouhým bleskovým nahlédnutím na stav portfolia v aplikaci mého mobilního telefonu. Co mohu ale říct o celkovém riziku portfolia, které má sto padesát obchodních pozic složených z podkladů a na ně navázaných derivátů, které společně nějakým způsobem korelují a navíc každý jednotlivý segment portfolia vykazuje jiný profil zisku a ztráty? Nic konkrétního, pokud nezapojím nějakou statistickou metodu nebo nepoužiji nějaký vhodný analytický nástroj, který mi pomůže nahlédnout na základní rizikové parametry mého portfolia. Je také jasné, že pokud bychom dostali společně s dalšími tradery za úkol utratit každý jeden milion dolarů „na nějaké investice“ na kapitálovém trhu, udělá to každý po svém a každý podstoupí při svém investování jinou úroveň budoucího rizika. Budou tedy muset existovat nějaké obecné nástroje, které by mohly takto různorodá rizika měřit na nějakém jednotném základě a za sjednocených principů, zejména proto, aby bylo možné tato rizika nějakým zodpovědným způsobem řídit. Pochopení základních nástrojů, které mi toto měření umožňují, pak mohu aplikovat na jakkoliv rozsáhlá investiční portfolia, od mého malého obchodního účtu až po obrovská multimilardová fondová portfolia.    

Portfolio RiskProfile

   Pokud bych měl své portfolio složeno z investičních nástrojů, které mají profil zisku a ztráty ve tvaru přímky (například nakoupené akcie), mohu odhadovat, jak se portfoliu povede, pokud trhy rostou nebo klesají například na základě metod, které budou využívat tzv. Beta, tedy číslo, které zobrazuje stupeň závislosti pohybu akciového titulu vzhledem k celkovému pohybu trhů, který se rozhodnu měřit například nějakým akciovým indexem. Obecně jsem o Beta psal v těchto článcích Beta – I. a Beta – II., nebudu se již nyní konstrukcí tohoto parametru zabývat. Pokud budu znát míru závislosti pohybu akciového titulu na vybraném akciovém indexu, mohu stanovit, jakým způsobem se změní hodnota mé investice do jednotlivého akciového titulu, pokud se hodnota referenčního akciového indexu pohne na jakoukoliv úroveň. Pokud budu na svém účtu držet několik akciových titulů s rozdílnou alokací a s rozdílnou Beta pro každý z nich, mohu metodou vážení jednotlivých Beta zjistit celkovou Beta mého portfolia. Mohu pak opět zjišťovat a odhadovat, nakolik se hodnota mého akciového portfolia změní, pokud se změní hodnota vybraného akciového indexu. Má celková investice do nakoupených akcií na mém obchodním účtu by pak vykreslovala nějakou pomyslnou přímku, která by charakterizovala profil zisku a ztráty v závislosti na pohybu příslušného akciového indexu, který jsem použil pro stanovení jednotlivých Beta mých nakoupených akciových titulů. Protože obchoduji u Interactive Brokers, mohu při sledování takové závislosti využít analytickou aplikaci Risk Navigator, která se spouští z panelu nástrojů obchodní platformy TWS.

   Spuštěním Risk Navigatoru mám možnost nahlédnout na základní parametry mého akciového portfolia z pohledu výše napsaných řádků, tedy mít možnost vyhodnotit, jaká je Beta mého portfolia.

   Mé akciové portfolio disponuje nyní celkovou Beta na úrovni 1.16. Znamená to, že je mírně vyšší než hodnota jedna a znamená to, že pokud se hodnota referenčního akciového indexu zvýší o jedno procento, vzroste hodnota mého portfolia o +1.16%, portfolio bude tedy velmi mírně volatilnější než je sledovaný akciový index, mnou vypozorované číslo je ale tak velmi blízko jedničce (dokonalá korelace s akciovým indexem), že jej mohu za takto ideálně korelované považovat. Ponechám nyní stranou techniku výpočtu Beta a zaměřím se na skutečnost, že analytický nástroj Risk Navigator mi může nabídnout různé hodnoty Beta pro mé akciové tituly podle nejrůznějších akciových indexů, mohu jednoduše pozorovat a vybrat, jaký akciový index je pro tento výpočet pro mě nejvhodnější. Tuto volbu mohu spustit v nabídce „Settings“

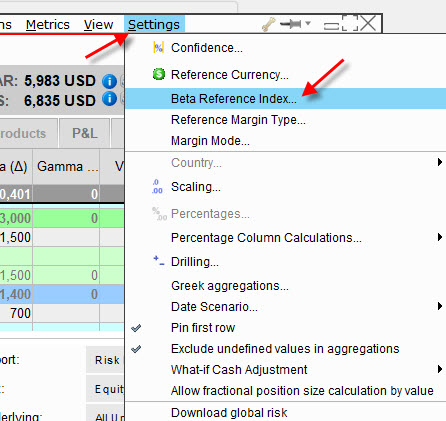
   Volbou „Settings“ a následně „Beta Reference Index…“ vyvolám nabídku pro volbu nejrůznějších akciových indexů.

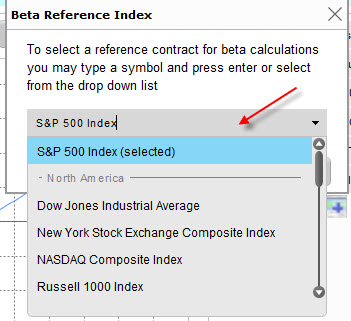
   Mohu vypozorovat, že mám vybránu volbu S&P500 Index, jako referenční index pro výpočet Beta mého portfolia, který je na úrovni 1.16. Mohu se pokusit svůj výpočet změnit a vybrat například Dow Jones Industrial Average akciový index. 

    Po potvrzení volby mohu pozorovat tuto změnu celkové Beta.

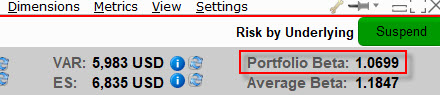
   Použití jednotlivých Beta mých akcií vypočítaných podle korelace s indexem Dow Jones Industrial Average mi přineslo přepočítanou celkovou Beta mého portfolia na úrovni 1.069, tedy ještě těsněji k hodnotě jedna než v případě Beta mého portfolia vypočítané podle indexu S&P500.

   Pokud by se tedy jednalo pouze o takto strukturované akciové portfolio, mohl bych tvar křivky profilu zisku a ztráty v grafické podobě vypozorovat v okně Risk Navigatoru takto:

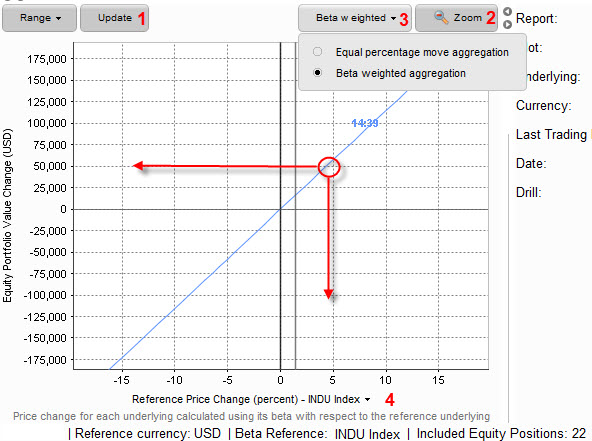
   Avizoval jsem RiskProfile ve tvaru přímky, která vykresluje závislost pohybu ceny mého akciového portfolia v závislosti na pohybu hodnoty indexu Dow Jones Industrial Average. Mohu si každou změnu v simulaci vývoje ceny portfolia promítnout do této křivky jejím znovunačtením (1) a přiblížením ve větším detailu (2). Mohu vybírat z nabídky závislosti na aplikaci vážené Beta (3), to je výběr učiněný v obrázku, tedy pohyb na akciovém indexu je přepočítán do pohybu na jednotlivém akciovém titulu podle své vlastní Beta podle vybraného indexu na rozdíl od druhé možnosti, která předpokládá stejný procentní pohyb pro všechny akciové složky portfolia bez ohledu na Beta. Ve spodní části grafu s profilem zisku a ztráty mohu odezírat celkový popisný komentář. Z obrázku je patrné, že pohyb na akciovém indexu Dow Jones Industrial Average o necelých +5% způsobí, že hodnota mého portfolia by se k okamžiku vyobrazení tohoto profilu změnila o +50.000 USD (červený kroužek v grafu), a protože má profil zisku a ztráty lineární profil, při stejně velkém poklesu bych mohl utrpět adekvátně stejně velkou ztrátu.

   Takto jednoduše graficky vyobrazený profil zisku a ztráty by již tak byl určitě dobrou pomůckou, jak zjistit, jak se bude mému portfoliu dařit, pokud se trhy měřené mnou vybraným indexem budou pohybovat. V mém případě se jedná o držení Long akciových pozic, takže směr přímky se dá velmi jednoduše interpretovat a odhadnout, rostoucí trhy znamenají blahodárný vliv na mé portfolio a naopak. Jak ale naložit s portfoliem, kde profily zisku ztráty pro jednotlivé investiční nástroje nejsou lineární a jejich pohyb nelze tak snadno odhadnout v závislosti na vybraném akciovém indexu, což platí zejména pro nejrůznější deriváty. Další komplikací pak může být obchodování nejrůznějších kombinací těchto derivátů najednou, kdy tyto kombinace mezi sebou vytvářejí nejrůzněji tvarované komplexní profily zisku a ztráty, které bych velmi pracně nějak manuálně zpracovával. RiskProfile pro takto komplexnější portfolio vykreslený pomocí grafického znázornění jeho křivky v Risk Navigatoru by pak mohl dát alespoň stručný obrázek o základních parametrech mého portfolia. Na obrázku níže je tento profil pro jedno z mých Delta Neutral portfolií, tedy kombinací podkladových aktiv plně zajištěných opčními kontrakty.

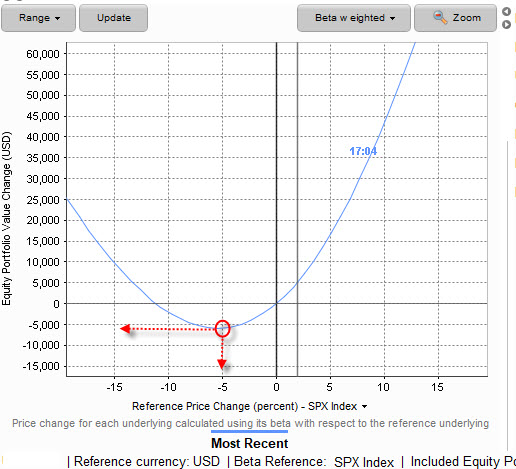
   Mohu vypozorovat, že jsem použil profil zisku a ztráty podle vážené Beta, kdy jsem si nechal zobrazit profil zisku a ztráty vztažený k pohybu akciového indexu S&P500. Nakoupené akciové podklady mám zajištěny nakoupenými Long opčními kontrakty, za které jsem vydal peníze, proto je dno tohoto profilu pod nulovou hranicí, která představuje náklady na toto zajištění. Mohu tak vypozorovat, že jsem zcela ochráněn při poklesu hodnoty portfolia ve výši propadu akciového indexu S&P500o zhruba o -11% a více, při menším propadu bych utržil maximální ztrátu přibližně -5.000 USD, na straně růstu hodnoty akciového indexu S&P500 bych pak mohl počítat také s vyobrazenými profity, pokud by se hodnota tohoto indexu patřičně pohnula směrem vzhůru . Musím tak konstatovat, že bych se pravděpodobně nebyl schopen nějakou vlastní metodou dobrat tak jednoduché vizualizace stavu mých pozic v danou chvíli s velmi čitelnými a jasně deklarovanými vyhlídkami.   

   Přestože je zobrazování profilu zisku a ztráty mého portfolia vskutku skvělá názorná pomůcka, chybí ji základní prvek politiky řízení rizika, tedy kvantifikace přesnější sumy peněz, kterou svými investicemi opravdu riskuji. Profil zisku a ztráty mi sice zobrazuje, jak to může s mým portfoliem dopadnout, pokud se trhy pohnou o nějaký definovaný kousek od chvíle, kdy jsem tento profil vytvořil, neříká to ale nic o tom, kolik bych mohl na investici vydělat/ztratit v nějakém časovém horizontu a jaká je pravděpodobnost, že se tak stane. „Obchoduj tak, aby tvé portfolio mohlo ztratit maximálně dvacet tisíc dolarů s pravděpodobností 5% během jednoho obchodního dne a je mi úplně jedno, do čeho budeš investovat“ by mohlo být zadání šéfa oddělení rizik v investiční firmě namísto toho, aby se prodíral drženým multipozicemi každého z třiceti obchodníků, kteří mu podléhají nebo aby alespoň prostudoval rizikové profily jejich portfolií. Bude mu pak stačit sledovat, při nastavené pravděpodobnosti pro zadaný časový úsek, úroveň ohroženosti vyřčené dvacetitisícové částky – maximální možné ztráty pro každé z portfolií, tedy sledovat tzv. VaR.

Value at Risk (VaR)

   Každá slušnější obchodní platforma by měla mít schopnost vygenerovat jeho uživateli hodnotu Value at Risk drženého portfolia, pokud budu moci nechat počítat tuto hodnotu podle nějakých volitelných parametrů, bude to jenom její další přidaná hodnota. Nezbývá potom než jen pochopit, jakou má takový výpočet hodnotu, jak jej zasadit do celkového kontextu řízení rizika, jak takový výpočet interpretovat a jaká je základní logika jeho výpočtu. Můj broker Interactive Brokers nabízí několik možností, jak k hodnotě VaR přistoupit, jak ji vypočítat a jak si ji zobrazit.

  V okně Risk Navigatoru mohu pro hodnoty Value at Risk vypozorovat následující nastavení.

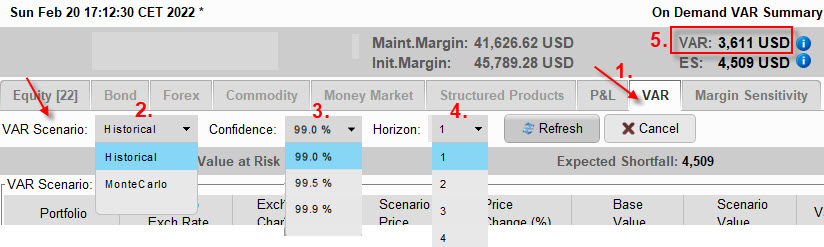
    Kliknutím na záložku VAR (1) mohu vypozorovat nastavení zobrazení hodnoty VaR pro mé obchodované portfolio. Na páse VAR Scenario (červená šipka) mohu volit způsoby, jak si VaR nastavit, první možností je vybrat metodu výpočtu (2) (Historical, Monte Carlo), nastavení úrovně spolehlivosti (pravděpodobnosti) (3), zde mohu vybírat ze tří úrovní 99%, 99.50% a 99.90% a nakonec mohu zvolit časový horizont (4), pro který chci hodnotu VaR zobrazit. Mé nastavení z obrázku znamená, že jsem si za pomocí metody „Historical“ s pravděpodobností 99.00% vypočítal hodnotu VaR pro jednodenní časovou úroveň a tato hodnota je nyní 3.611 USD (5). Znamená to, že (za použití této výpočetní metody) s pravděpodobností 1% mohu za jeden den ztratit částku -3.611 USD a vyšší nebo opačná interpretace, s pravděpodobností 99% mohu během následujícího obchodního dne očekávat pohyb hodnoty mého portfolia o částku -3.611 USD a vyšší. Jak jsem k takové interpretaci došel bude patrné z ukázky, jak si takovou historickou hodnotu VaR vypočítat pro nějaké malé fiktivní portfolio.

Historická metoda VaR

   Rozhodl jsem se, že nakoupím 100x Long akcií CAT a 100x Long akcií KMB. Pro toto mé miniportfolio budu chtít stanovit hodnotu VaR historickou metodou pro pravděpodobnost 1% s horizontem jednoho obchodního dne. Bude mě jednoduše zajímat, o kolik by mohlo mé portfolio s touto jednoprocentní pravděpodobností přijít během jednoho obchodního dne. Historická metoda výpočtu VaR je založena na historických pohybech jednotlivých složek portfolia, jejich setřídění a vyhodnocení podle zadaných podmínek. Pro potřeby mého výpočtu jsem si tedy opatřil pětiletá historická data obou akciových titulů na finance.yahoo a tyto přenesl do mého excelu.

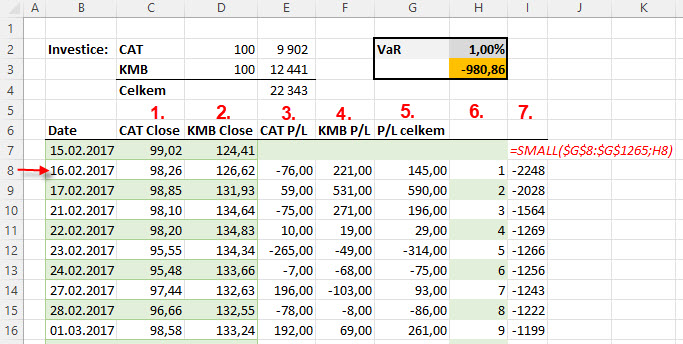
  V excelu jsem poté pro oba tituly ponechal pouze sloupce pro denní Close ceny (1) a (2). Protože se mi jedná o jednodenní hodnotu VaR, vypočítal jsem si pro jednotlivé tituly z mého portfolia mezidenní výnosy každé složky. Mohu tak na první řádku s výpočtem (červená šipka) vypozorovat, že pokud bych portfolio nakoupil před pěti lety 15.2.2017 za Close ceny před uzavřením trhů, následující den by mých sto akcií CAT ztratilo na hodnotě -76 USD (3) a naopak stovka akcií KMB by přinesla profit +221 USD (4), celkově bych pak svůj účet obohatil (-79 USD +221 USD) o částku +145 USD (5). Takto vypočítám výnos/ztrátu pro každý den za celé pětileté období. Provedené výpočty v tabulce seřadím od nejnižšího po nejvyšší pomocí číselné řady (6), kterou použiji do vzorce ve sloupci (7). Tento postup jsem již popisoval v článku Volatilita a cenový pohyb – II., nebudu se nyní již jeho popisem zabývat. V tomto posledním sloupci pak vidím pod sebou jednotlivé jednodenní výnosy od nejvyšší ztráty až po největší celkový profit. Takto seřazené jednodenní profity/ztráty mohu pak ilustrovat pomocí histogramu.

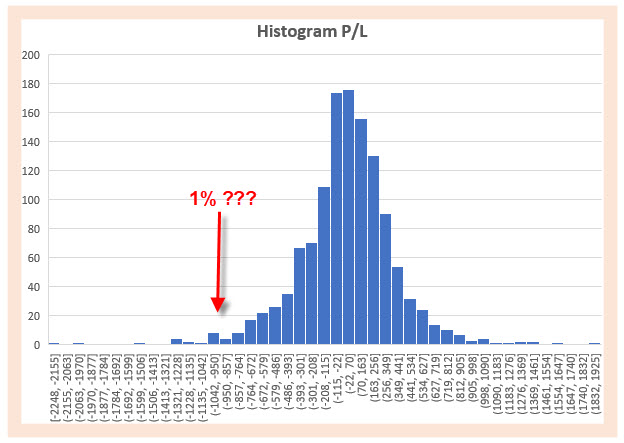
    Mohu se nyní přesvědčit, že v jednotlivých cenových intervalech se vyskytuje vždy určitý počet výskytů reprezentovaný výškou modrého sloupce. Mohu pak vypozorovat, že nejvíce hodnot je „namačkáno“ kolem středu histogramu, který reprezentuje jakousi průměrnou hodnotu a představuje velmi malé jednodenní pohyby. Nejpravděpodobněji tak budou jednodenní výnosy nebo ztráty velmi malé, mohu také pozorovat, že vyšší výnosy nebo vyšší ztráty se mému miniportfoliu nevyhnuly a jsou představovány sloupci odlehlejšími od pomyslného vrcholu histogramu. Na obou koncích histogramu pak mohu pozorovat extrémní profity nebo extrémní ztráty, protože je ale výška sloupců nepatrná, mohu očekávat jejich vzácnější výskyty. Dalším výsledkem pozorování provedeného seřazení je skutečnost, že maximální profit představoval částku +1925 USD a maximální ztráta činila -2248 USD, je tak zřejmé, že na straně ztráty existuje „tlustější ocas“ mého histogramu.

   Z vyobrazeného rozložení mých seřazených výsledků bude nyní nutné určit, jaký výsledek mohu očekávat podle mého zadání pro stanovení jednodenního VaR 99%. Ten bude reprezentovat takovou hodnotu, která bude hodnotou percentilu na úrovni 1%, tedy hraniční úrovní, která všechny denní výnosy, které jsem seřadil a reprezentují 100% mých naměřených výnosů, rozděluje na část intervalu o velikosti nula až jedno procento a zbylý interval jedno procento až sto procent. V histogramu toto reprezentuje červená šipka, pro kterou budu hledat její skutečnou hodnotu z mých zjištěných výsledků jednodenních profitů nebo ztrát.

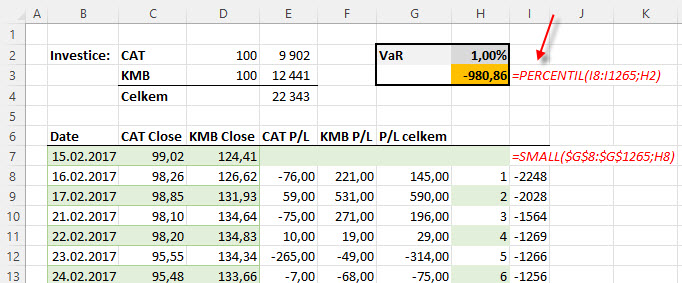
   Nalezení hodnoty takového zadaného percentilu není nic obtížného, excelovská funkce =PERCENTIL umí z vybrané oblasti dat vybrat právě takovou hodnotu a tuto pak mohu interpretovat jako hledaný VaR podle mého zadání pro mé fiktivní portfolio. Mohu tak provedením výpočtu zjistit, že historickou metodou vypočítaný jednodenní VaR 99% na úrovni -980.86 USD znamená, že s pravděpodobností 1% mě může při zítřejším obchodování postihnou ztráta -980.86 USD a vyšší. Mohu také prozkoumat, jak se změní VaR, pokud změním hodnotu pravděpodobnosti, k takovému zkoumání si vyberu například hodnotu VaR 95% (5% pravděpodobnost) nebo hodnotu VaR 99.50% (pravděpodobnost 0.50%).

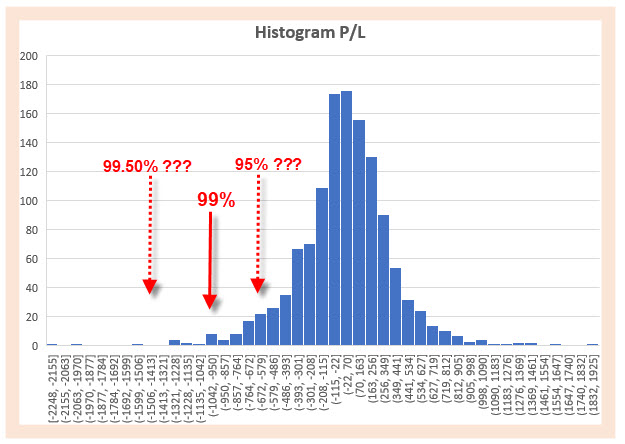
   Pokud již vím, jaká je hodnota jednodenního VaR s pravděpodobností 1% (VaR 99%) počítaný historickou metodou (-980.86 USD), měl bych být schopen alespoň předběžně odhadnout, zdali pro tyto jiné úrovně spolehlivosti bude hledaný VaR vyšší nebo nižší než mnou prozatím identifikovaná hodnota pro pravděpodobnost 1%. Z histogramu totiž vyplývá, že čím více se budu posunovat ve hledání na levou stranu grafu, budu nacházet vzácnější výskyty větších ztrát, budu tedy muset očekávat, že pokud budu hledat VaR pro „jemnější“ pravděpodobnost (například 99.50%), bude hodnota VaR vyšší, pokud budu směřovat svou pravděpodobnost směrem ke středu histogramu, bude hodnota VaR nižší. Mohu toto například vyzkoušet na mém obchodním účtu, kde jsem do Risk Navigatoru zadal zjištění VaR 99.90%.

   Protože hodnota 99.90% leží ve větší vzdálenosti od středu histogramu než původní hodnota 99% (VaR -3.611 USD), budu očekávat, že jeho hodnota bude vyšší, což se také z obrázku výše potvrzuje. VaR na hladině spolehlivosti 99.90% mého portfolia je na hodnotě -5.945 USD a je tak o více než dva tisíce dolarů vyšší. Mohu pak toto aplikovat také na excelovský výpočet mého fiktivního portfolia a vypočítat hodnotu VaR pro 99.50% a 95% namísto 99%.

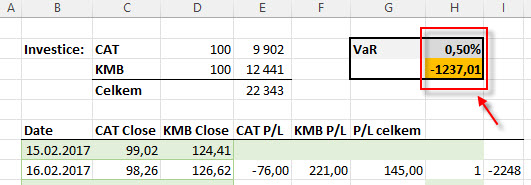
   Výpočet VaR pro spolehlivost 99.50% přinesla vyšší hodnotu -1.237 USD než byla pro pravděpodobnost 99%, protože se nachází ve větší vzdálenosti od středu histogramu, které reprezentuje vyšší jednodenní ztráty. Naopak také mohu zobrazit VaR pro úroveň pravděpodobnosti 95%, která se bude nacházet blíže středu histogramu.

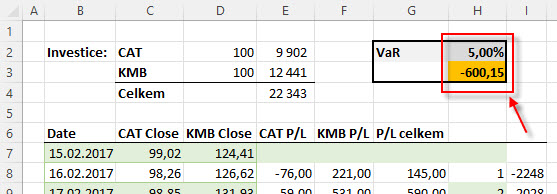
   Hodnota VaR s pravděpodobností 95% na úrovni -600.15 USD je nižší než pro VaR s pravděpodobností 99% (-980.86 USD) nebo 99.50% (-1.237 USD), protože se nachází v oblasti, které reprezentují menší mezidenní ztráty. Je tedy nyní na mě, abych se rozhodl, jakou úroveň VaR budu pro své vyhodnocení rizika používat a jaká úroveň pravděpodobnosti mi více vyhovuje. V obecném pohledu na výše napsané řádky pak budu muset vzít v úvahu, že vyšší procentní úroveň VaR bude znamenat sice méně pravděpodobnou možnost výskytu ztráty, tato však bude při této menší pravděpodobnosti vyšší. Pokud bych chtěl tuto myšlenku měření rizika zapojit do praxe u mého portfolia, tak bych při zjištění VaR například se spolehlivostí 99% podle této metody a v jednodenním horizontu s úrovní -980.86 USD, mohl chtít mít právě takto vysokou možnou ztrátu zajištěnou nějakým investičním nástrojem nebo pozicí, která by ji mohla při nepřízni vývoje pokrývat.        

   Pohledem na obrázek histogramu s četností výskytu jednotlivých mezidenních profitů a ztrát bych mohl zaznamenat, že tvar jednotlivých sloupců bych mohl pospojovat do nějaké spojnice a vykreslit v jejich vrcholech křivku, která by byla velmi nápadně podobná křivce hustoty pravděpodobnosti Normálního rozdělení (Gaussova křivka), jak jsem ji popisoval například v článku Základy tradingové statistiky – II.. Mohl bych pak přistoupit ke zjištění VaR „více statisticky“ a nechat si příslušné hodnoty VaR vyhodnocovat jinou metodou. Hned v úvodu poznamenám, že historická metoda výpočtu VaR má proti této „vědečtější“ metodě zásadní výhodu, a to je respektování existence „tail risku“, tedy možnosti více ztratit při poklesu než vydělat při růstu, protože jednotlivé výskyty významnějších ztrát se nalézají v odlehlejší oblasti vzhledem ke středu grafu než významnější profity na opačné straně histogramu četnosti podle popsané historické metody.

   Ze získaných pětiletých dat mého excelu použitého pro mé miniportfolio simulující držení akcií CAT a KMB, mohu vypočítané mezidenní profity a ztráty podrobit zjištění, jakou mají střední hodnotu a jakou hodnotu standardní odchylky. Budu jednoduše předpokládat, že mezidenní pětileté výnosy mají Normální rozdělení s vypočítanou střední hodnotou a zjištěnou standardní odchylkou. Pokud zjistím tyto parametry mého miniportfolia (nebo jakéhokoliv portfolia) a budu předpokládat, že jednodenní výnosy mají Normální rozdělení, budu schopen stanovovat jednotlivé pravděpodobnosti výskytu nejrůznějších mezidenních profitů a ztrát a tyto interpretovat také jako VaR, ale odlišnou metodou. Mohu si pak nechat zobrazit namísto histogramu křivku hustoty pravděpodobnosti výskytu profitů a ztrát v takto zjednodušeném tvaru.

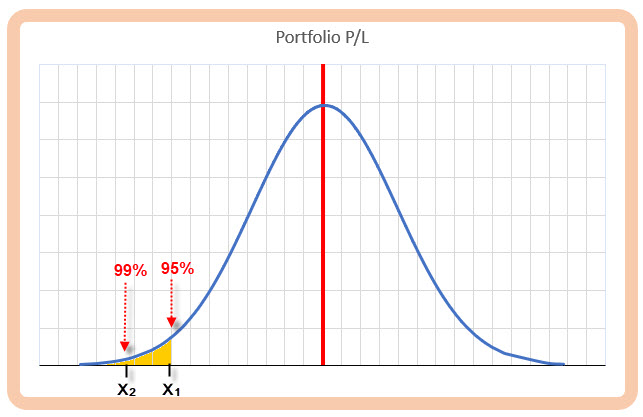
   Protože vycházím z předpokladu, že mé mezidenní výnosy portfolia mají Normální rozdělení, mohu těmto jednotlivým výnosům (ztrátám a profitům) přiřadit pravděpodobnost, s jakou se mohou vyskytnout. Z možnosti přiřadit určité hodnotě náhodného jevu pravděpodobnost vyplývá také obrácená možnost, tedy zjišťovat velikost této hodnoty, pokud budu znát její pravděpodobnost, a o to v případě VaR také jde. Na obrázku mám vyznačeny požadované hodnoty pravděpodobnosti jednodenních zisků a ztrát mého portfolia (95% a 99%) a budu k nim hledat příslušné hodnoty konkrétních ztrát X₁ a X₂ (pohybuji se na levé straně grafu), které těmto hodnotám odpovídají. Není to nic náročného, excelovská funkce =NORM.INV takovou hodnotu pro zadané Normální rozdělení s konkrétní střední hodnotou a danou standardní odchylkou umí vypočítat. Na obrázku níže je výpočet jednodenního VaR touto metodou pro pravděpodobnost 99%.

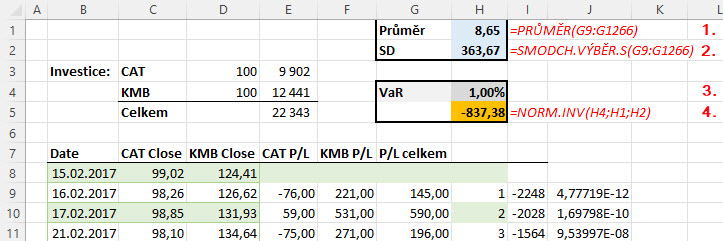
   Výpočet průměru (1) ze zjištěných jednodenních profitů a ztrát není potřeba komentovat, stejně tak excelovské zjištění hodnoty standardní odchylky těchto hodnot (2). Tímto mám definovány základní parametry rozdělení těchto hodnot a mohu je využít ke hledání konkrétních hodnot podle zadaných pravděpodobností. V obrázku hledám hodnotu ztráty, která představuje VaR 99% (3), tedy hodnotu ztráty s pravděpodobností přesně 1%, toto mohu opět interpretovat jako konstatování, že s pravděpodobností 1% utrpí mé portfolio ztrátu, která bude stejná nebo vyšší než nalezená hodnota ztráty, tato pak činí -837,38 USD (4). Mohu tak nyní porovnat obě metody a zjistit, že historickou metodou jsem vypočítal jednodenní VaR 99% na částku -980.86 USD, kdežto statistickou metodou za použití Normálního rozdělení představuje jednodenní VaR 99% částku -837,38 USD, tedy o stopadesát dolarů částku nižší. Znamená to avizovanou přesnější předpověď pravděpodobnosti ztráty pomocí historické metody, ta totiž bere v úvahu historickou skutečnost, že ztráty mého miniportfolia mohou být v jednodenním měření větší než případné profity („tail risk“). Zajímavé srovnání přináší zjištění VaR oběma metodami na „velkorysejší úrovni“ VaR 95%

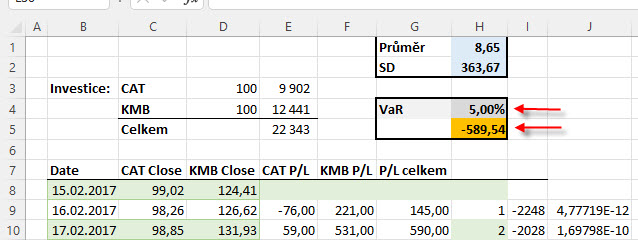
   Historickou metodou zjištěný jednodenní VaR 95% na úrovni -600.15 USD pak silně koresponduje se zjištěnou hodnotu jednodenního VaR 95% pomocí zjednodušené statistické metody, která jej stanovila na hodnotu -589,54 USD, rozdíl je pak pouhých cca 10 USD. Mohu si to vysvětlit tak, že se zvyšováním pravděpodobnosti pak bude mé portfolio dosahovat průměrně stejných výsledků počítaných podle obou metod, snižující se pravděpodobnost, která pracuje s méně obvyklými výskyty jednotlivých ztrát, pak bude přinášet odlišnější výsledky. Vycházení z předpokladu, že jednodenní výnosy mého portfolia by mohly mít pravděpodobnost výskytu podle Normálního rozdělení mohu využít k další práci se stanoveným VaR. Stanovení hodnoty konkrétní ztráty s konkrétní pravděpodobností v horizontu jednoho obchodního dne pak mohu velmi jednoduše rozšířit na očekávání možné ztráty se stejnou pravděpodobností na jakékoliv budoucí období. Pokud je tedy můj VaR 99% vypočítaný statistickou metodou na hodnotě -837.38 USD a představuje 1% pravděpodobnost přijmout za následující obchodní den ztrátu v této výši nebo dokonce vyšší, mohu tento požadavek rozšířit na početní úkol stanovit hodnotu této ztráty při dané pravděpodobnosti na jeden týden (pět obchodních dnů) nebo například na jeden měsíc (21 obchodních dnů).

   Popisu, jak stanovit z jednodenní hodnoty Implied Volatility tuto hodnotu pro delší časový úsek jsem se věnoval v článku Volatilita a cenový pohyb – I.. Šlo o prosté vynásobení jednodenní hodnoty Implied Volatility odmocninou času, pro který hledám příslušnou Implied Volatilitu, mohu tak z její procentní hodnoty, která představuje pravděpodobnost cenového pohybu pro zadaný časový úsek, odvozovat velikost cenového pohybu opčního kontraktu. Stejně si mohu počínat v případě výpočtu utržení možné ztráty při určité pravděpodobnosti za libovolné období, která bude vycházet z hodnoty ztráty za stejné pravděpodobnosti pro jednotku času (například den).         

   Jednodenní VaR 99% se zjištěnou hodnotou -837.38 USD vypočítaný statistickou metodou mohu přepočítat na týdenní VaR 99% vynásobením odmocninou z 5, která představuje 5 obchodních dnů tvořících následný obchodní týden, abych zjistil, že během následujícího týdne (nebo jakýchkoliv následujících pět obchodních dnů) mohu s pravděpodobností 1% ztratit na mém akciovém miniportfoliu částku -1.875,73 USD a vyšší. Použitím odmocniny libovolného času pak mohu odhadovat možnosti ztráty pro jakékoliv období.

  Monte Carlo metoda VaR

   „Co bylo, už není“. Předvídání budoucnosti na základě zkušeností z minulosti je základní, pochopitelný a vskutku logický princip nikoliv pouze v běžném životě, ale také v matematice a statistice. Odrazy minulých zážitků se v mozku transformují do aktuálních interakcí na realitu, která mě obklopuje a vznikají tak každodenní unikátní řešení stejného rutinního problému. Přestože jsem přesvědčen, že jedu se svým autem do práce stejnou cestou, stejně rychle a se stejnou samozřejmostí, každá jízda patrně vykazuje nějaké drobné odchylky od „zavedené rutiny“, jakéhosi pomyslného průměru, která je reakcí na nové události, které aktuálně během jízdy nastaly. Školáci na přechodu, psaní SMS, námraza na vozovce, zapomenuté brýle nebo jen obyčejná snaha „dneska dodržovat rychlost“ vtiskne do této jízdy neopakovatelné prvky, které ve výsledku svých možných kombinací s vlastní pravděpodobností znamenají různě dlouhý čas, který jsem tomuto zcela běžnému úkonu věnoval. Ve světle těchto skutečností pak mohu zjištění hodnoty VaR podle metod popsaných výše považovat za jakousi pravděpodobnost, odvozenou od součtu jevů, které se v minulosti opravdu staly, které se ovšem v budoucnosti nemusí vůbec opakovat. „Co bude, nikdy nebylo“ pak může být zcela jednoduchá formulace motivů pro využití metody Monte Carlo pro zjištění hodnoty VaR. Jejím základním principem je možnost provést z nashromážděných dat pro konkrétní zjištěnou datovou řadu zcela náhodnou záměnu těchto dat a vytvoření nové datové řady, která by mohla být jedním z budoucích scénářů možného vývoje. Pokud se mi podaří vyrobit značné množství takových náhodných řad, mohu z jejich možného průběhu usuzovat na nějaké kvalitativní ukazatele možného budoucího vývoje. Metoda Monte Carlo se tak snaží vyjádřit „Brownův pohyb“ mého miniportfolia směrem do budoucnosti, tedy jakousi „náhodnou procházku“, na kterou mohu se svými nastřádanými daty vyrazit.    

   Ke zjištění VaR jsem u předcházejících metod vycházel ze skutečně zjištěných pětiletých mezidenních pohybů mého miniportfolia akcií KMB a CAT, které původní investici do stovky akcií z každého titulu v celkové výši 22.343 USD nakonec zhodnotily na úroveň 33.226 USD. Vysledované pětileté období (konkrétně 15.2.2017 – 14.2.2022) přineslo celkem 1258 konkrétních mezidenních pohybů, jejichž výsledkem byla právě výše uvedená výkonnost. Tento pevně stanovený sled mezidenních pohybů, tak jak se skutečně v minulosti odehrál, přinesl výpočet hodnoty jednodenního VaR 99% pomocí historické metody částku -980,86 USD a pomocí statistické metody hodnotu jednodenního VaR 99% částku -837,38 USD.

   Risk Navigator obchodní platformy TWS nabízí možnost nechat si zobrazit jednodenní VaR s 99% pravděpodobností také právě pomocí Monte Carlo metody. Znamená to, že možnost ztráty s nějakou pravděpodobností (1%) v horizontu jednoho obchodního dne je založena právě na simulaci historických dat pomocí tohoto statistického nástroje. Přestože je mnoho možností, jak k simulaci Monte Carlo, tedy výpočtu VaR touto metodou přistoupit (koneckonců můj broker podstatu takového výpočtu nezveřejňuje), mohu se pokusit ukázat, jak bych mohl takovou metodu „nasadit“ na mé miniportfolio a pokusit se proniknout do podstaty této metody pomocí Excelu. 

   Z historických pětiletých dat mého portfolia jsem zjistil skutečnosti zobrazené níže na obrázku.

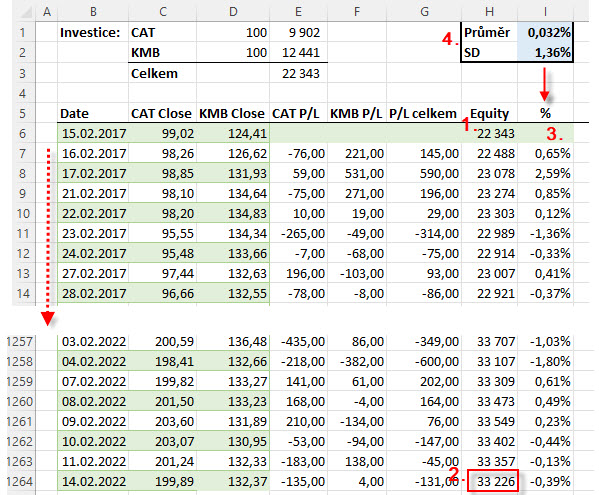
   Pětiletá historie mého miniportfolia rozprostřená na více než tisícovce řádků ukazuje, že jsem opravdu svou investici 22.343 USD (1) zhodnotil na částku 33.226 USD (2). Jednotlivá mezidenní výkonnost miniportfolia je pak zobrazena ve sloupci (3). Mohu pak z této výkonnosti vypočítat její střední hodnotu s úrovní 0.032% a standardní odchylku ve výši 1.36% (4). Za předpokladu, že tyto jednodenní výkony mají Normální rozdělení, není nic obtížného stanovit jejich výši pro jakoukoliv mnou zvolenou pravděpodobnost, což bylo předmětem statistické metody určení hodnoty VaR, kterou jsem výše popisoval. Má snaha bude vygenerovat další možné datové řady, které by napodobovaly parametry tohoto originálního a skutečného historického vývoje. Zapojení náhody do excelovské tabulky vyžaduje nasazení excelovské funkce =NÁHČÍSLO (). Její umístění do buňky v excelu vytvoří v této buňce náhodně vygenerované desetinné číslo z intervalu nula až jedna.

   Mohu pak tyto desetinná čísla považovat například za náhodně vygenerovanou pravděpodobnost výskytu „něčeho“, tato pravděpodobnost výskytu se také pohybuje pouze v intervalu 0% až 100% a nemůže být jiná. Zapojení náhodného čísla k vytvoření náhodné datové řady provedu podle obrázku níže.  

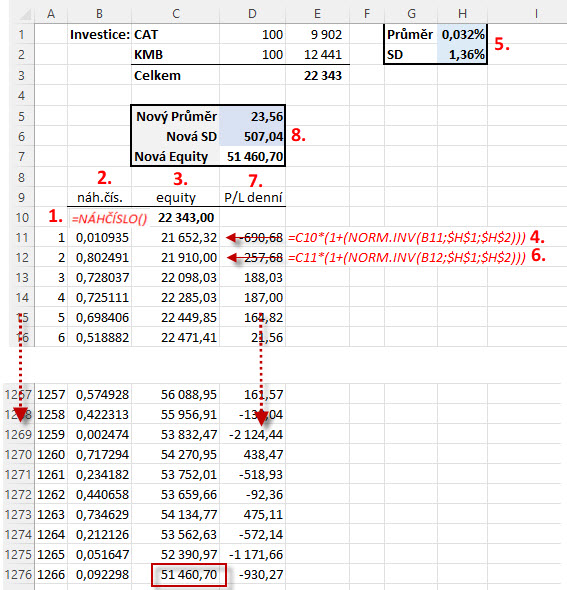
   Původní datovou řadu pětiletého vývoje mého miniportfolia jsem měl rozmístěnou v excelovské tabulce na 1266 řádcích. Označím si proto novou tabulku, kde budu generovat náhodnou časovou řadu, čísly řádků 1 – 1266, abych pokaždé vygeneroval stejný počet dat nové náhodné řady (1). Ve sloupci „B“ vygeneruji podle již známe formule náhodná čísla, která budou představovat nahodilou pravděpodobnost (2). Ve sloupci „C“ budu vytvářet náhodnou datovou řadu (3), prvním číslem v buňce „C10“ je startovací hodnota mé investice (23.343 USD). První hodnota mé náhodně vytvářené datové řady v buňce „C11“ (21.652,32 USD) je vytvořena pomocí vzorce pro vyhledání hodnoty inverzní funkce pro Normální rozdělení (4), tedy budu hledat hodnotu mezidenního výnosu mého miniportfolia pro zadanou pravděpodobnost (náhodná pravděpodobnost generovaná náhodným číslem v buňce „B11“) pro datovou řadu, která předpokládá Normální rozdělení s parametry (střední hodnotou a standardní odchylkou) mého původního a skutečně zjištěného historického vývoje mého miniportfolia (5). Tento vypočítaný náhodný výnos pak připočtu k hodnotě mé startovací sumy. Takto postupuji v generování jednodenních náhodných výnosů i na dalších řádcích (6) až vyplním do buněk ve sloupci „C“ všech 1266 nových náhodných postupných hodnot mého miniportfolia. Takto získám nové mezidenní výnosy pro tuto nově vygenerovanou náhodnou datovou řadu (7).Tato nová data řada pak disponuje nově vypočítanými vlastnostmi (8), mohu pak vypočítat její novou průměrnou střední hodnotu (23.56), novou standardní odchylku (507.04) a novou hodnotu celkové equity (51.460,70 USD). Každé stisknutí klávesy „F9“ na mé klávesnici provede nové generování sady náhodných čísel, mohu pak pozorovat novou křivku náhodné equity a samozřejmě také nové rozložení mezidenních výnosů ve vytvořených grafických vizualizacích. Ve videu níže je zobrazeno opakované mačkání klávesy „F9“ spojené s generováním náhodných datových řad.

   Modrá křivka reprezentuje datovou řadu mezidenních výnosů tak, jak se opravdu v historii vyskytovaly ve svém přesném chronologickém průběhu. Červená křivka pak zachycuje datovou řadu vygenerovanou pomocí náhodných čísel, které představují náhodnou pravděpodobnost výběru ze spektra mezidenních výnosů s Normálním Rozdělením s vlastnostmi tohoto historického průběhu. Na změně histogramu je pak patrné, že každá náhodná výnosová křivka disponuje jiným rozložením mezidenních výnosů, bude tak jasné, že hodnota ztráty s pravděpodobností 1% (VaR 99%) bude pro každou vygenerovanou řadu odlišná. Mohu pak tento VaR 99% pro každou takovou řadu vypočítat.

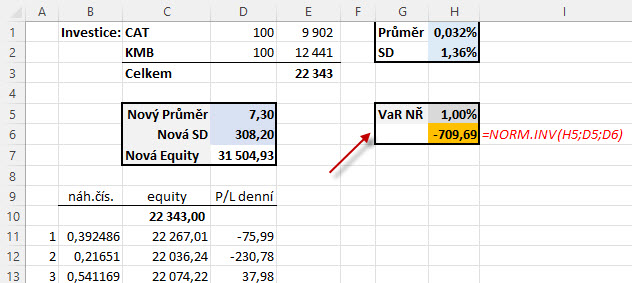
   Z obrázku zjišťuji, že pro aktuálně vytvořenou náhodnou řadu mohu vypočítat hodnotu VaR 99% na úrovni -709.69 USD (označeno VaR NŘ – VaR Náhodné Řady). Podstatou metody Monte Carlo je pak vytvořit obrovské množství podobných simulací se zabudovanou náhodou a zjišťovat, jak se může pro tyto náhodné budoucí vývoje měnit mnou pozorovaný parametr, nyní tedy VaR NŘ 99%. Budu tedy chtít provést alespoň jeden tisíc takových budoucích náhodných vývojů mého miniportfolia a z těchto průběhů pak vždy zaznamenat jenom hodnotu VaR 99% u každého jednotlivého z nich. Zprůměrováním jednoho tisíce získaných „VaRů 99%“ pak vypočítám VaR 99% na základě tisícinásobné simulace Monte Carlo.

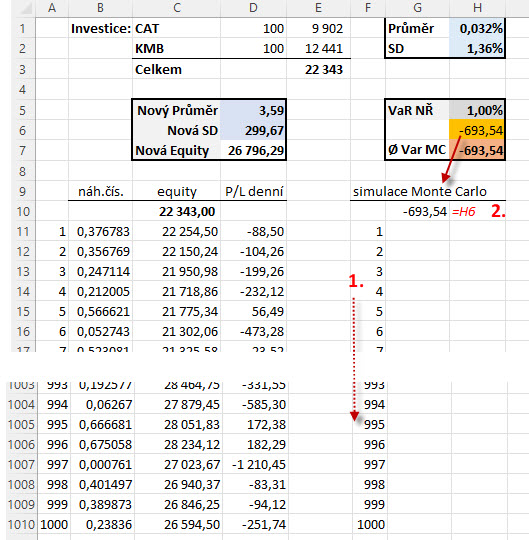
   Ve svém excelu vytvořím ve sloupci „F“ sloupec s čísly 1 – 1000, který bude označovat jeden tisíc budoucích simulací (1). Do vedlejšího sloupce „G“, do první buňky nad začátek řady, kde budu chtít zaznamenávat výsledek prováděných simulací (2), přenesu vzorec s výpočtem, který po simulacích požaduji. V mém případě budu chtít zaznamenávat VaR 99% z každé náhodné řady, kterou postupně vytvořím (a bude jich rovná tisícovka). Poté provedu akci podle obrázku níže.

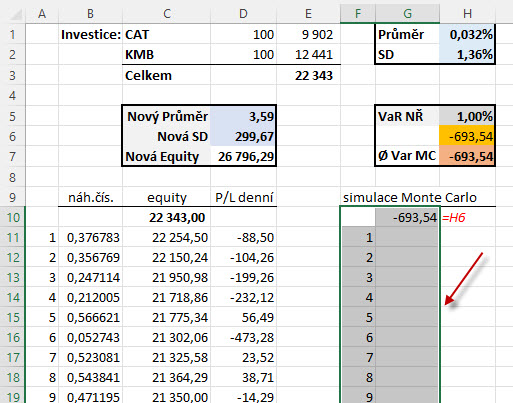
   Tažením myší označím oblast dat zahrnující sloupec s čísly 1 – 1000 a sloupec s přenášením požadovaných výpočtů, kde je v první buňce jeho vzorec. Poté vyberu ke zpracování výpočtu vhodný excelovský nástroj.

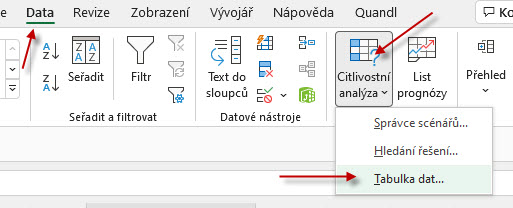
   Ze záložky „Data“ vyberu „Citlivostní analýza“ a potvrdím „Tabulka dat…“. Touto volbou otevřu parametry datové tabulky, kterou mám označenu tažením myší výše.

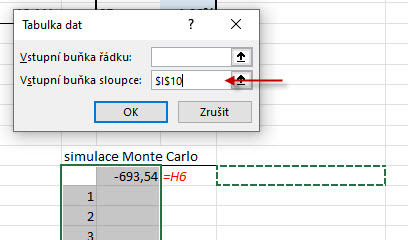
   Do „Vstupní buňka řádku“ nevkládám nic, do „Vstupní buňka sloupce“ zadám například buňku „I10“. Potvrzením „OK“ dojde k automatickému vyplnění všech označených buněk výpočtem VaR 99% pro jeden tisíc simulací.

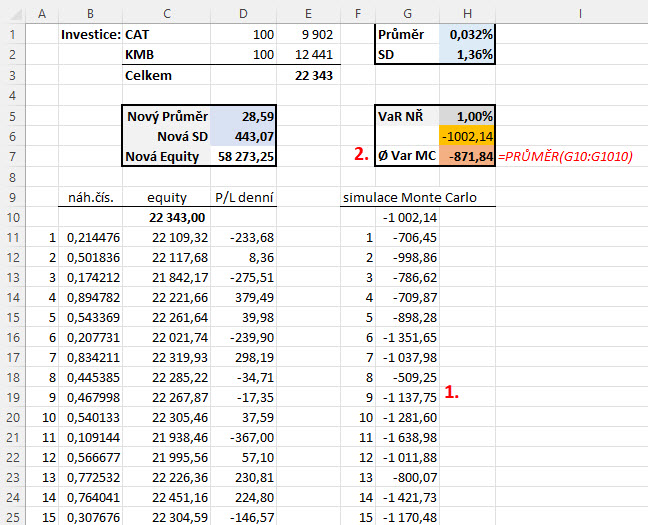
   Provedením tisícovky simulací (1) dojde k výpočtu průměrné hodnoty VaR 99% pomocí těchto mnohonásobných simulací. Mohu tak z obrázku odezírat, že s pravděpodobností 1% může mé portfolio utrpět během následujícího dne ztrátu -871.84 USD a vyšší, toto vše vypočteno pomocí metody Monte Carlo (2) založené na tisícovce simmulací. Mohu pak kliknutím na klávesu „F9“ provést další tisícovku jiných simulací…Je pak také jasné, že změnou hodnoty hledané pravděpodobnosti mohu velmi jednoduše stanovovat jednotlivé VaR pro tyto pravděpodobnostní úrovně.

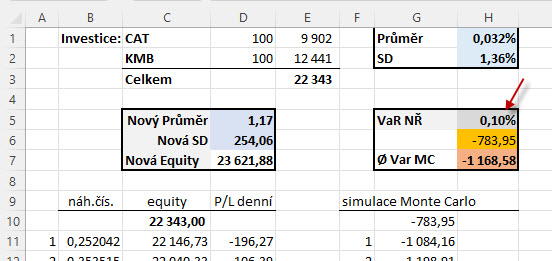
   Zjištění VaR 99.90% pro mé miniportfolio metodou Monte Carlo s tisícovkou simulací by stanovilo hodnotu ztráty -1.168,58 USD a vyšší s pravděpodobností 0.10% pro následující obchodní den.

   Jak nakonec takové zacházení s VaR vyhodnotit? Je velmi důležité si uvědomit, že výpočet VaR je postaven na pravděpodobnosti, vycházím pouze z dat, která představují nějaký minulý vývoj a z něj se snažím usuzovat do budoucnosti. Co se v minulosti stalo, se samozřejmě v budoucnosti neopakuje, toto sice mohu nahradit nějakými náhodnými simulacemi, vždy jde ale pouze o nějaký odhad a v tomto smyslu by se k VaR mělo přistupovat. Nesmím samozřejmě zapomenout vzít v úvahu kvalitu historických dat, která budu zpracovávat, jejich nepřesnost může způsobit značné rozdíly ve výstupních výpočtech a mohou potom zavádějícím způsobem ovlivňovat řízení rizika portfolia. Jak bych se k vypočítané konkrétní hodnotě VaR postavit? Pokud přijmu za své, že budu sledovat hodnotu VaR 99%, tedy připustím pravděpodobnost 1% nějaké konkrétní ztráty v následujícím obchodním dni, měl bych patrně vytvořit alespoň takové zajištění, které by mohlo takovou ztrátu v mezidenním horizontu krýt, jaké by mohlo konkrétně být, ponechám na fantazii každého obchodníka.

   Zcela zásadní otázkou je pak vyhodnocení vypočtené hodnoty VaR v její absolutní výši. Pokud jsem vypočítal jednodenní VaR 99% pomocí metody Monte Carlo na úrovni -871.84 USD a tato metoda a tato pravděpodobnost mi bude vlastní, musím nyní prozkoumat, jestli je z hlediska řízení rizika přijatelná či nikoliv. Samotné číslo o míře rizika nevypovídá téměř nic, proto jej musím uvést do nějaké logické souvislosti. Pokud jsem investoval 22.343 USD, potom hodnota jednodenního VaR 99% na úrovni -871.84 USD představuje možnou ztrátu -3,90% z investované částky s pravděpodobností 1% v následujícím obchodním dni. Neumím posoudit, jaký je práh bolestivosti risk manažera nebo konkrétního tradera, tedy jestli je s touto možnou ztrátou mentálně srovnán natolik, aby ji vyhodnotil jako přijatelnou nebo absolutně nepřípustnou. Mohu pak také hodnotu jednodenního Var 99% na hladině -871.84 USD vztáhnout nikoliv k investované částce, ale k hodnotě mého investičního účtu, který je například 70.000 USD, potom by taková jednoprocentní pravděpodobnost ztráty činila -1.25% z celého mého obchodního účtu a bylo by pak opět na vyhodnocení, jestli je to mnoho nebo málo. Jako příklad posouzení hodnoty VaR mohu použít dokument jisté nadnárodní investiční společnosti, která na hodnotu VaR nahlíží takto: „..The one day 95 percentile Value at Risk (VaR) based on the standard normal distribution of the aggregate net exposure of the Investments may not exceed 1.5% of the Investment Account Value at any given time…“ V jednoduchém vyjádření tak definují riziko jednodenní hodnotou VaR 95%, jehož hodnota nesmí překročit 1.5% hodnoty investičního účtu. Jak by tedy mohl reagovat riskmanažer této investiční společnosti na nenadále turbulence na trzích? Jednoduchým příkazem uděleným podřízeným obchodníkům o snížení daného jednodenního VaR 95% na částku představující pouze 1% každého z investičních účtů. Tradeři, kteří by tuto hranici na svých účtech překračovali by pak museli jít domů nebo snížit expozici svých pozic na požadovanou novou úroveň pro VaR 95%.     

   Je patrné, že definovat riziko není zrovna jednoduché, zejména u komplexnějších portfolii. Zabudované statistické nástroje, kterými disponuje Interactive Brokers však mohou být velmi dobrým pomocníkem, jak tuto definici usnadnit. Cílem článku tak bylo provést nějakou základní náhled na strukturu možných výpočtů nebo alespoň jejich logiku. V úvodním příspěvku ve fóru k tomuto článku lze stáhnout excel s výpočty, které jsem výše popisoval  :c) 

Komentáře a příspěvky k tomuto článku prosím směrujte do Diskuzního fóra do tohoto vlákna :c)