Je pondělí 25.3.2019 a já sleduji třetí díl čtvrté série kultovního seriálu Billions. Taylor rozepisuje na tabuli matematickou úvahu, která demonstruje spletitost, složitost a sofistikovanost vydělávání peněz na finančních trzích. Snaha je pravděpodobně ukázat, že pokud to nemáte v hlavě matematicky v pořádku, nemáte šanci se takovým investorským veličinám rovnat.

   Tejlořin táta, jako spoluautor rozepsaného televizního matematického chuchvalce, nakonec prohodí něco o úchvatnosti Frobeniovy věty a máte jasno, že je zcela nemožné proniknout do světa „velkých financí“ bez tak elementární znalosti, jako je existence a aplikace Frobeniovy záležitosti. V investiční praxi totiž nebudete dělat nic jiného, než řešit soustavy lineárních rovnic a zjišťovat, kolik mají vlastně řešení pomocí této nezbytné matematické vychytávky. Frustrace z neznalosti doprovázená pocitem méněcennosti je tady a zbývá tedy řešit již jen technické otázky, tedy, kdy zavřu svůj obchodní účet a jaké úroky mi vlastně nyní nabízí stavební spoření s vychytralou liškou. Je tomu opravdu tak, že to bez nějakého „vyššího poznání“ matematiky nelze zvládnout? Odpověď je vcelku jednoduchá, zcela jistě! Je to přece jenom seriál z atraktivního prostředí a jde převážně o to ukázat, nakolik mají hlavní hrdinové „sexy mozky“. Přestože je Frobeniova věta jednou z nejdůležitějších vět lineární algebry, mám obavu, jestli tvůrci tohoto seriálu své diváky nějakým důmyslným způsobem nezmátli, protože dotyčný výpočet na tabuli neunikl špionážnímu foťáku Bobbyho Axelroda, který si nakonec zálibně prohlíží pořízený snímek výpočtu v útulném prostředí svého tryskáče.

   Nejsem nějaký matematický zarputilec a možná se mnou takto erudovanější čtenáři nebudou souhlasit, ale vyobrazený matematický traktát, rozepsaný na formátu zhruba jeden čtvereční metr, nemá s danou matematickou problematikou, tedy hledání řešení soustavy lineárních rovnic, mnoho společného (pokud vůbec), proto si takového nesouladu musel samozřejmě všimnout i samotný Bobby.

   Nemá proto dále cenu pro hlavního hrdinu se v takových výpočtech pitvat a je lepší se zaměřit na praktičtější disciplínu, jako by například mohlo být falšování Arkansaského Chicken Indexu a vsadit na prozaičtější investiční metody. Je to tak nakonec stejné jako v samotném životě, tedy jaké si to kdo udělá, takové to nakonec bude mít, někomu stačí povrchní znalosti a má nadmíru odvahy k obchodům, jinému nebude vadit hlubší poznání, ze kterého by mohl čerpat a objevovat komplexnější řešení, které mu třeba vykompenzuje nedostatek nezbytného obchodního odhodlání. Geniální mozky mezi obchodníky opravdu existují a brilantní znalosti z širokého spektra oborů jsou opravdu skvělou výbavou pro pochopení složitějších tržních souvislostí než jen těch opravdu nejelementárnějších nebo těch, které jsou patrné na první pohled, nikoho ale automaticky nepředurčují k lepší obchodní výkonnosti.

    Zpátky do reality a k Delta Neutralitě. Z dosavadních publikovaných článků prozatím vyplynulo, že Delta Neutralita vytváří nezávislost pohybu ceny opčního kontraktu na pohybu podkladového aktiva, tato ale není trvalejšího charakteru a je porušována permanentními pohyby podkladového aktiva. Odklony od Delta Neutrality vytvářejí obchodní příležitosti, na které se mohu dívat pomocí dalších „řeckých písmen“, když jsem se v dosavadních článcích zabýval Gamma, jako odvozeninou Delta a vypozoroval jsem její vliv na portfolia podle jejího znaménka. Zkoumání kladné Gamma je pak dosavadním hlavním motivem prozatím napsaného. Začíná se také rýsovat hrubá představa o práci s Delta a Gamma, jako o výrazných parametrech při práci se zajišťováním opčních pozic na mém účtu, kdy jsem velmi efektivně schopen vhodnými operacemi s podkladovými aktivy kompenzovat časovou složku hodnoty opčního kontraktu při současných vyhlídkách na velmi slušný profit vyplývající z možného velmi slušného pohybu podkladu. Myslím si, že již nyní je patrné, že provádění takových úprav portfolia je určeno pro velmi opatrné obchodníky, kteří dbají na osud svých investic a ve světle úvodu článku se pak nyní budu snažit matematicky takovou dbalost a odpovědnost také podpořit. Po dvou praktických článcích s konkrétními obchody tedy opět něco ryze teoretického.

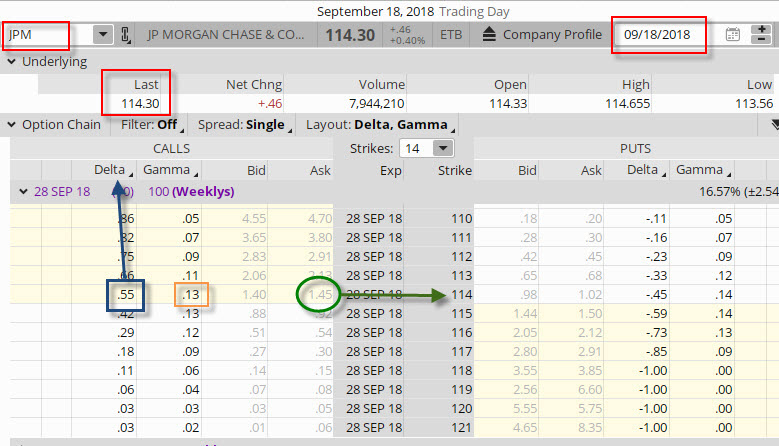
   Složité věci mě neberou, složitosti mám tendenci zjednodušovat, jak se to jenom dá, na druhou stranu ale troška matematiky také ještě nikoho nezabila. Ve starších článcích o Delta a Gamma jsem popisoval matematickou formu těchto písmen odvozenou od Black-Scholesova oceňovacího modelu, společně s jejími interpretacemi. Také jsem naznačil, jakým způsobem jsou z Black-Scholesova oceňovacího modelu odvozeny a jak se dají vypočítat. Delta a Gamma mohu také matematicky interpretovat pomocí derivací. Derivace funkce v obecném matematickém pohledu vyjadřuje změnu hodnoty funkce v závislosti na změně nezávislé proměnné (argumentu), pokud je změna hodnoty funkce závislá na jedné proměnné, pak se jedná o parciální derivaci. Vypadá to složitě, ale o co vlastně jde? Na obrázku níže je vyobrazena funkce ceny Long Call opčního kontraktu na strike 114 podkladové akcie JPM.

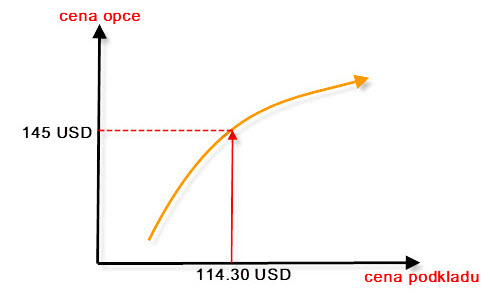
   Tato funkce by mohla mít například tento tvar a z něj by mohlo vyplývat, že cena Long Call opčního kontraktu bude klesat tak, jak klesá hodnota akcie JPM a bude proto vydatně ztrácet na hodnotě, naopak, pokud cena akcie roste, cena Long Call opčního kontraktu se zvyšuje až dospěje do fáze, kdy je růst ceny podkladu identický k růstu ceny podkladu – o kolik vzroste cena podkladu, o tolik se zvýší cena opčního kontraktu (Delta opce = 100). Graf zobrazuje závislost ceny opčního kontraktu pouze na pohybu podkladového aktiva (akcie JPM) a nezahrnuje žádné další vlivy – běh času, změnu Implied Volatility, vyplácenou Dividendu nebo změnu úrokové míry, její průběh je nyní závislý pouze na jediné proměnné, kterou je změna ceny podkladu. Z obrázku pak mohu vypozorovat, že cena Long Call opčního kontraktu bude mít při ceně akcie JPM na úrovní 114.30 USD hodnotu 145 USD. Pomocí matematické definice derivací pak mohu konstatovat, že hodnota Delta je první derivací funkce ceny opčního kontraktu v závislosti na ceně podkladového aktiva. Mohu si pak tento matematický zápis zobrazit níže takto:

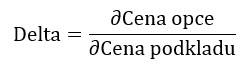
   Uvedenou derivací pak zjistím, že pro danou funkci závislosti ceny opčního kontraktu na ceně podkladu platí, že při ceně podkladové akcie JPM na úrovni 114.30 USD má Long Call opční kontrakt na strike 114 cenu 146 USD a hodnota Delta +55.

    Gamma je popisována jako číslo, které vyjadřuje, o kolik se změní Delta v závislosti na změně ceny podkladového aktiva, měří tedy nikoliv změnu ceny opčního kontraktu (i když se toto dá samozřejmě vypočítat) ale změnu Delta, tedy vypočtené hodnoty z výše uvedeného vzorce. Při použití stejného obrázku funkce změny ceny opčního kontraktu v závislosti na ceně podkladové akcie tak mohu matematicky konstatovat, že Gamma je druhou derivací funkce ceny opčního kontraktu v závislosti na ceně podkladového aktiva. Takový pohled na Gamma pak mohu formulovat do matematického zápisu níže.

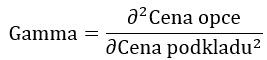
   Mohl bych také ve stejném smyslu vytvořit třetí derivaci funkce ceny opce v závislosti na změně ceny podkladového aktiva a zjišťovat, jak se mění velikost samotné Gamma, tuto odvozenou hodnotu bych pak mohl nazvat pracovně například „jiřina“, abych zachoval ženský rod řeckých písmen zachycujících závislost na pohybu podkladu (Delta, Gamma, Jiřina…:c) a mohl bych se také vrhnout na čtvrtou derivaci atd. Zůstanu ale u takto matematicky zachycených hodnot Delta a Gamma a tyto pak využiji k přiblížení základního obchodního pohledu na Delta Neutralitu a roli Gamma mého portfolia. Abych vrátil takový náhled na Delta Neutralitu do konkrétního příkladu, mohu využít situaci na podkladové akcii JPM ze dne 18.9.2018.

    Při ceně akcie JPM na úrovni 114.30 USD (toto je ve výše uvedených vzorcích označeno jako „Cena podkladu“) jsem měl možnost nakoupit Long Call opční kontrakt na strike 114 za cenu -145 USD (ve vzorcích označeno „Cena opce“). Delta tohoto Long Call 114 opčního kontraktu je vypočtena na hodnotu +55, proto jsem pořídil, pro potřeby Delta Neutrality, -55x Short akcií JPM za cenu 114.30 USD/kus. Nyní mě bude zajímat, jak vypočítám svůj profit na nakoupené Long Call 114 opci, které je neutralizovaná Short akciemi, pokud nastane nějaký pohyb na akcii JPM. Pokud bych zjišťoval tento profit například na druhý den po vstoupení do výše uvedené pozice, kdy mohu již vědět, jaký pohyb na podkladové akcii opravdu nastal a jak se v důsledku tohoto pohybu změnila cena mé Long Call 114 opce, mohl bych si takový výpočet profitu matematicky zapsat například takto:

   Není to nic nepochopitelného, odečetl bych od nové dnešní ceny opčního kontraktu jeho pořizovací (včerejší) cenu (Cena opce nová – Cena opce) a zjistil bych, jak jsem na opci vydělal/prodělal. Od této hodnoty bych odečetl, kolik vydělaly/prodělaly mé Short akcie (∂Cena opce/∂Cena podkladu * změna Ceny podkladu), když výraz „∂Cena opce/∂Cena podkladu“ reprezentuje výše uvedený matematický zápis pro Delta a potažmo tedy počet pořízených Short akcií JPM.

   Pokud bych tedy aplikoval tento jednoduchý vzorec na můj případ, tak bych mohl zjistit, že se cena akcie JPM výrazně pohnula směrem nahoru a v mezidenním srovnání přidala +3.32 bodu, aby vystoupala do Close druhého dne od pořízení celé pozice na cenu 117.62 USD.

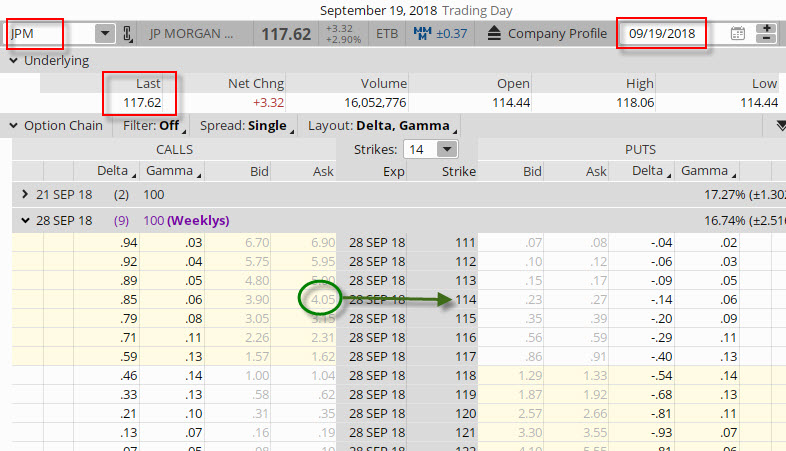
   Uptrend ceny akcie JPM ze 114.30 USD na cenu 117.62 USD způsobil zvýšení ceny Long Call 114 opčního kontraktu z pořizovací ceny 145 USD na cenu 405 USD. Aplikací vzorce pro výpočet profitu při tomto jednodenním pohybu tak mohu zjistit, že „Cena opce nová – Cena opce“ činí 405 USD – 145 USD = +260 USD, což reprezentuje profit na nakoupeném Long Call 114 opčním kontraktu. Akcie však na své hodnotě ztratily, „∂Cena opce/∂Cena podkladu * změna Ceny podkladu“ mohu nahradit „Delta (vlastně počet Short akcií) * změna ceny podkladu“, tedy (-55*3,32 USD) = -182.60 USD a tato hodnota pak reprezentuje ztrátu na držených Short akciích. Můj celkový profit z této jednodenní transakce je pak (+260 USD – 182.60 USD) ve výši +77.40 USD.

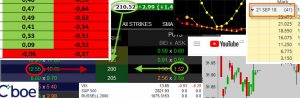
   Toto je ale již konkrétní a pochopitelný výpočet pro konkrétní obchodní situaci s nakoupenou Long Call opcí, která nastala. Od profitu na opci odečtu ztrátu na akciích (pokud cena akcie vzrostla) nebo ke ztráty na opci přičtu profit na akciích (pokud cena klesla), nic složitého k pochopení. Já ale budu chtít demonstrovat obecný matematický příklad výpočtu profitu mého Delta Neutral portfolia a budu chtít ukázat, jakou v něm hraje roli Gamma. Pro tuto matematickou interpretaci budu vycházet ze stejné úvahy jednoduchého výpočtu celkového profitu portfolia a bude mě zajímat, jaká bude hodnota mého profitu, pokud se cena podkladové akcie pohne o nějaký obecně definovaný kousek. Například to bude znamenat, že jsem si své portfolio podle obrázku z platformy TOS pořídil při ceně akcie na úrovni 114.30 USD a bude mě zajímat, jaké budu mít profity nebo ztráty, pokud se cena akcie JPM bude pohybovat v nějakých cenových pásmech. Abych mohl takovou věc vyřešit a vypočítat, musím znát, jakou bude mít při těchto změněných cenách akcie JPM, novou hodnotu můj opční kontrakt Long Call 114, pokud jej budu schopen stanovit, budu pak schopen použít jednoduchý výpočet profitu mé pozice (od profitu na opci odečtu ztrátu na akciích a je vypočítáno). Problémem ovšem je stanovit právě novou cenu opčního kontraktu Long Call při změně její ceny, sice jsem naznačil, že existuje jakási funkce změny ceny v závislosti na ceně podkladové akcie, ale její průběh jsem načrtl víceméně naslepo a nemohu z něj cokoliv přesného odvozovat. Mohl bych si tento problém zobrazit graficky jako na níže uvedeném obrázku.

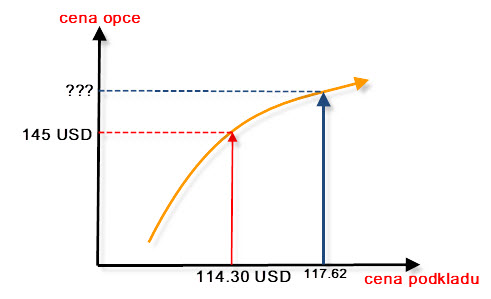
    Obrázek ukazuje, že nyní přesně vím, jaká je hodnota Long Call opce na strike 114, když cena podkladu je 114.30 USD, nevím ale, jaká bude cena této opce při teoretickém uptrendu například na cenu 117.62 USD. Nevím totiž, jestli jsem oranžový průběh cenové křivky zakreslil správně, jestli cenovou změnu nevykresluje jen přibližně nebo je věcí pouze náhodného a intuitivního nákresu. Přestože ale nemám k dispozici přesný průběh této cenové křivky, tak mám čísla, které jsou její první a druhou parciální derivací – Delta a Gamma.

   Matematika si s takovou situací umí poradit. Pokud existuje jakási funkce závislosti ceny opce na pohybu podkladu (a ona existuje, pokud cena podkladu roste, tak cena opci taktéž a naopak), pak mohu pomocí derivací určit, jaká bude přibližná hodnota této funkce ceny na jiné úrovni ceny podkladového aktiva. Pomocí Taylorovy řady (ne, nemá to s Taylor z Billions nic společného, pouze je mou asociací pro tento článek) mohu nahradit průběh této cenové funkce  pomocí mocninné řady a stanovit tak cenu opčního kontraktu na jiné cenové úrovni po pohybu podkladu s určitou přesností. Taylorův rozvoj pomáhá nahradit cenovou funkci a svou konstrukcí (podle svého řádu) umí přibližovat průběh funkce co nejblíže hledanému výsledku, a protože jsem Delta a Gamma interpretoval pomocí první a druhé parciální derivace, vytvořím Taylorův polynom druhého řádu právě za využitím známé první a druhé derivace funkce ceny opce. Má tento tvar:

   No, vypadá pravděpodobně hrozně, ale není tomu ve skutečnosti tak. Mohu totiž vypozorovat, že hodnoty s derivacemi jsou vlastně již známé hodnoty Delta a Gamma  a „změna Ceny“ je hodnota cenového pohybu, pro který chci vypočítat novou hodnotu ceny opčního kontraktu. Tento složitý vzorec pak mohu zjednodušit náhradou zlomků s derivacemi hodnotami Delta a Gamma, abych vypozoroval toto zjednodušení níže.

  To se mi to pěkně zjednodušilo, jenom co je pravda. K provedené úpravě pak jen dodám, že „reziduum“, které jsem z původního vzorce vypustil je malé číslo, které nehraje v této abstrakci významnou roli. Nová hodnota opčního kontraktu po „nějakém pohybu“ reprezentovaném ve vzorci hodnotou „změna Ceny“ se pak vlastně vypočítá jako původní (pořizovací) „Cena opce“, ke které připočítám hodnotu Delta vynásobenou změnou ceny podkladové akcie a dále připočítám jednu polovinu hodnoty Gamma vynásobenou druhou mocninou změny ceny podkladové akcie. Toto je již velmi elegantní řešení, při kterém nemusím nic derivovat, jedná se pouze o základní matematické operace sčítání, odčítání, násobení a dělení.

   Pokud bych nasadil tento jednoduchý vzorec na můj konkrétní případ z 18.9.2019 na akcii JPM, mohl bych vyjít z toho, že v tento den měla Long Call opce na strike 114 hodnotu 145 USD, Delta +55 a Gamma +13. Akcie JPM se obchodovala za 114.30 USD. Do druhého dne (19.9.2018) posílila na hodnotu 117.62 USD. Do vzorce bych pak dosadil původní pořizovací hodnotu opčního kontraktu Long Call 114, Delta, Gamma a změnu Ceny podkladové akcie JPM, tedy konkrétně: Cena opce = 145, Delta = +55, Gamma = +13 a změna Ceny = +3.32 USD (117.62 USD – 114.30 USD), potom, podle výše uvedeného zjednodušeného vzorce pro výpočet nové ceny opce:

   Cena opce nová = 145 + (55*3.32) + (13*(3.32)² /2)  = 399.24 USD

   Z obrázku z platformy TOS výše vyplývá, že nová cena opčního kontraktu po pohybu o +3.32 USD na akcii JPM činí 405.00 USD, což jé téměř identická hodnota, jako podle mého výpočtu za pomoci Taylorova polynomu, rozdíl je způsoben Ask/Bid spreadem a působením dalších cenotvorných okolností.

   Nyní jsem tedy schopen, pomocí matematických operací, zjistit hodnotu ceny opčního kontraktu na libovolné jiné ceně, tedy určit závislost ceny opce na pohybu podkladového aktiva, stačí k tomu znát aktuální hodnotu Delta a Gamma. Mě však ale stále zajímá, jakým způsobem se změní hodnota profitu mého portfolia, které je nyní Delta Neutrální, při jakékoliv teoretické cenové změně ceny podkladové akcie JPM a co mi těchto profitech říká Gamma. Sumarizace této úvahy je pak na níže uvedeném obrázku.

   1/ První vzorec je původním vzorcem výpočtu profitu pro Delta Neutrální portfolio, kde znám cenu opce původní a také cenu opce po změně ceny podkladového aktiva, tedy od změny ceny opce odečtu změnu ceny hodnoty podkladů a mám jednoduše vypočtený profit, toto je vcelku jasná formule.

   2/ V předcházejícím původním vzorci pro výpočet profitu jsem nahradil zlomek s derivacemi hodnotou Delta. Nyní se chci ale nacházet ve fázi čisté matematické úvahy, kde neznám novou hodnotu opce po změně ceny podkladu, ale již jsem zjistil, pomocí Taylorova rozvoje, jak takovou novou hodnotu opce vypočítám, je totiž uvedena na následujícím řádku obrázku (č.3).

   3/ Výpočet ceny opčního kontraktu po pohybu ceny podkladu pomocí Taylorova polynomu a následném zjednodušení, které jsem prováděl podle obrázku výše, tedy za zlomky s derivacemi jsem dosadil výrazy Delta a Gamma.

   4/ Nejdůležitější část úvahy. Dosadil jsem celý výraz „Cena opce nová“ z předchozího řádku (č.3) do vzorce výpočtu profitu Delta Neutral portfolia z řádku č.2. Vznikl složitější algebraický útvar, který však nabízí stejné členy ke krácení, protože se objevují s opačnými znaménky.

   Výsledkem takových matematických úprav, náhražek výrazů a následného krácení je pozoruhodný závěr, ke kterému jsem se chtěl dobrat.

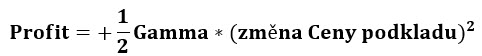
   Profit Delta Neutral portfolia je odvozen od jeho celkové Gamma podle tohoto vztahu. Mohu si jeho správnost ověřit na konkrétním případu s akcií JPM z 18.9.2019, kdy v tento den měla Long Call opce na strike 114 hodnotu 145 USD, Delta +55 a Gamma +13. Akcie JPM se obchodovala za 114.30 USD. Do druhého dne (19.9.2018) posílila na hodnotu 117.62 USD, posílila tak o +3.32 USD. V článku výše jsem vypočítal, za pomocí znalosti nové ceny opčního kontraktu Long Call 114, že po tomto uptrendu budu mít profit +77.40 USD (od výdělku na opcích jsem odečetl prodělek na akciích), to jsem ale mohl provést za předpokladu, že vím i novou cenu opčního kontraktu po uptrendu ceny, mě však bude zajímat kontrola výpočtu profitu bez této znalosti budoucí ceny opce, abych případně mohl dosazovat změny ceny podkladu podle libosti. Dosadím proto do nyní zjištěného vzorce aproximace profitu Delta Neutral portfolia podle Gamma konkrétní hodnoty:

Profit = (13*(3.32)² /2) = +71.64 USD

  Vypočítaný profit se od výpočtu profitu zjištěného podle skutečně nastalého pohybu a známých cen opcí před a po pohybu liší nepatrně o necelých šest dolarů, a to je skvělé zjištění. Mohu nyní modelovat dopady celkové Gamma portfolia na nejrůznější tržní situace a vypočítávat profity nebo ztráty, které to pro mé portfolio přinese. 

  Proč?

   Proč jsem se tímto problémem vůbec tak obšírně zabýval? Proč mi stálo za to se prodírat nějakými vzorci a sledovat obecný vliv Gamma na Delta Neutral portfolio? Protože jeho tvar dává odpověď na otázku, co mohu od takového portfolia vlastně očekávat a stačí mi k němu prozatím znát opět pouze hodnotu Gamma. Ďábel se totiž skrývá v mocninném tvaru změny ceny podkladu konečného vzorce. Můj profil profitu totiž nebude s profilem pohybu podkladu v lineárním vztahu ale právě naopak. Mohu si představit, že při této Gamma +13 mého velmi malého a jednoduchého portfolia Long Call 114 a -55x Short akcií se cena podkladu pohne do zítřejšího dne o jeden dolar. Potom bude celkový profit:  

   Profit = (13*(1.00)² /2) = +6.5 USD

   Malá změna ceny podkladu nebude mít na hodnotu portfolia valný vliv a portfolio bude stále dobře chráněno proti pohybu podkladového aktiva, bude samozřejmě trpět jinými riziky plynoucími s běhu času a změny Implied Volatility, ale proti pohybu bude stále slušně zajištěno. Pokud se však cena podkladu pohne výrazně, například o pět dolarů, bude hodnota profitu následující:

Profit = (13*(5.00)² /2) = +162.50 USD

   Profit roste nelineárně a je podstatný, pětinásobně vyšší pohyb ceny podkladu přinesl dvacetipětinásobný vyšší profit. Tento matematický zápis výpočtu profitu a schopnost interpolace profitu podle celkové Gamma portfolia by mělo být základním stavebním kamenem úvahy, proč vlastně vytvářet Delta Neutral portfolia a co mohu od takových portfolií čekat. Tento matematický zápis samozřejmě funguje také pro zápornou Gamma a vytváření Delta Neutral portfolií se zápornou Gamma nebo obecně Gamma negativních portfolií a měl by tak být mementem, že pokud se cena podkladu nepohybuje valně, působí na takové portfolia příjemné vlivy rozpadu časové složky nebo změny Implied Volatilty, pokud se ovšem cena značně změní, může být „nelineární vliv“ hodnoty Gamma na takto Gamma negativní portfolio devastující …:c)  

Sleduj facebook, napiš e-mail nebo tweet