Poznání principů Delta Neutral obchodování ve všech nuancích není jednoduché, přestože se to tak může na první pohled zdát. V předchozích článcích jsem popisoval, jak lze od sebe odlišit takové obchody například podle hodnoty znaménka u parametru Gamma a se zaslouženou pozorností jsem v několika dalších článcích popisoval obchodování na bázi pouze kladné Gamma. V článku Delta Neutral – VI. jsem se chtěl matematicky dobrat k demonstraci, že obchody se zápornou Gamma mohou být velmi špatně „řiditelné“ a mohou být zdrojem nemalého rizika vyplývajícího s neočekávaně velkého pohybu podkladu. Téměř všechny tyto články se pak nesly v duchu Delta Neutrality založené na pozorování, jak může mé portfolio ohrozit případný pohyb podkladového aktiva, v případě opčního portfolia s kladnou Gamma pak demonstrace pokusů, jak z těchto pohybů naopak těžit, protože toto je těmto obchodům vlastní a svou podstatou se k tomu takové úpravy vybízejí. V duchu mírného připomenutí základních poznaných principů Delta Neutrality a chování poznaných řeckých písmen jsem pak popsal, jak mohu pomocí práce s podkladem „regulovat“ Delta mé opční pozice a dodávat tak potřebné množství Delta k zabezpečení chtěné a požadované neutralizace. Bylo popsáno, že pokud má portfolio kladnou Gamma, bude každá taková úprava a manipulace s podkladem znamenat pro opční portfolio vždy nějaký částečný profit, v případě opčního portfolia se zápornou Gamma pak bude taková transakce znamenat vždy potvrzení nějaké částečné ztráty. Vypořádal jsem se tak nějakým způsobem s pochopením těchto transakcí a zejména s poznáním, jak pohyb podkladu působí na mé opční pozice. Pohyb podkladu ale není to jediné, co má na mnou pořízené opční kontrakty bezprostřední vliv a vytváří další risk. Existují další „externí vlivy“, které na mé opční portfolio působí současně s pohybem a jsou možným zdrojem dalšího rizika. Pochopení Delta a Gamma pak bylo rozvinuto do vykreslení základní souvislosti rizika vyplývajícího z pohybu podkladu a rizika způsobovaného plynutím času v tomto článku. V obecném shrnutí pak bylo konstatováno, že pokud mám opční portfolio s kladnou Gamma a z tohoto titulu vyplývajícím luxusem vydělávat na pohybu podkladu, tak mi toto přidělené štěstí kazí záporná Théta, tedy nutnost čelit riziku vyplývajícího z plynutí času, které každým dnem rozkládá hodnotu mého portfolia. V opačném principu pak záporná Gamma mého portfolia sice trpí značným rizikem vyplývajícím z pohybu podkladu, ale je okořeněno výhodou vyplývajícím z plynutím času – kladnou Théta, kdy takto koncipované portfolio získává na své hodnotě uplynutím každého dne jeho života. Tento poznatek je pak přenesen do skutečnosti, že hodnota znaménka Gamma u opčního kontraktu je vždy opačná než hodnota její Théta, mohu se tak pomocí tohoto opačného vztahu znamének Gamma a Théta pokoušet současně eliminovat také riziko plynutí času, toto není žádný nadlidský výkon. Každý velký pohyb a následná úprava portfolia do stavu Delta Neutrality s kladnou Gamma pak znamená také eliminaci záporné Théta tohoto portfolia, každý uběhlý den bez úpravy do stavu Delta Neutrality pro portfolio se zápornou Gamma znamená prospěch z kladné Théta tohoto portfolia.
V úvodu do tématu Delta Neutrality jsem uvedl, že opční portfolio na mém účtu trpí nejméně trojrozměrným riskem a tento je tvořen a vyplývá z pohybu podkladu (Delta, Gamma), plynutí času (Théta) a změny Impĺied Volatility (Vega). Každý tento risk nebo jejich kombinace může mít na mé portfolio blahodárný nebo devastující vliv, záleží, jaké má vlastnosti. Také jsem podotkl, že pokud poznám principy obrany proti těmto rizikům, mohly by z nich vyplynout nějaké smysluplné obchodní konsekvence. Mohu tak například chtít své portfolio mít zajištěno proti pohybu podkladu a nechat pracovat čas a Implied Volatilitu, mohu mít pokryto riziko vyplývající z plynutí času a nechat pracovat pohyb a Implied Volatilitu. Toto vše pak mohu povýšit na snahu kombinovat pokusy o hedžování dvou rizik a nechat pracovat riziko třetí v můj prospěch.
Logickým vyvrcholením článků o Delta Neutralitě by pak mohl být pokus o kombinaci současného zajištění portfolia proti riziku vyplývajícího z pohybu podkladu a rizika plynutí času za současného otevření se pokusu zobchodovat riziko vyplývající z pohybu Implied Volatility. Musím hned v úvodu tohoto zajímavého přístupu sdělit, že je to velmi nelehký úkol a úplně ideálně toto obchodovat jednoduše nejde, byť by to mohla být opravdu fantastická myšlenka.
Jak je to možné, že to nejde? No, možná to někomu jde, já to ale nedokážu a mám proto své velmi praktické důvody. Z předcházejících článků zejména vyplynulo, že Delta Neutralita je věcí mnohdy prchavého okamžiku, protože podklady se jednoduše pořád nějak pohybují a pokud bych byl extrémista, tak bych takovým pohybům mohl přisoudit vlastnosti Brownova pohybu, tedy neřešitelnost tyto pohyby nějak smysluplně kvantifikovat. Rovněž čas plyne pořád, na rozdíl od nepohybu podkladu ve chvílích, kdy se s ním neobchoduje, je plynutí času trvalé a nezastavitelné (i o víkendech – škoda…:c). Z této neuchopitelnosti času a dialektiky neustále změny ceny tak není možné obě tyto rizika zcela pevně „ukotvit“ a zajistit se v pozicích tak, abych mohl zcela jednoznačně spoléhat na to, že třetí riziko bude pracovat v můj prospěch. Pokud jsem nakoupil ATM Long Call opci na strike 120 při ceně akcie 115 USD a Delta mé opce je +35, tak mohu prodat -35x Short akcie a budu Delta Neutrální. Cena akcie ale zítra vystoupá na 120 a Delta mé Long Call 120 opce bude +50 a já již nebudu Delta Neutrální, ale budu muset prodat dalších -15x Short akcií. Jestliže tato Long Call 120 opce ztratila na své hodnotě od včerejška -7 USD vlivem plynutí času, tak se mohu spolehnout, že do zítřka ztratí další část své hodnoty. V minulých článcích bylo popsáno, jak tyto rizika poznat a také částečně řešit v naznačených ukázkách a obchodech. Nic ale není dokonalé a také obchodování touto technikou není záruka profitability, mohu tak k těmto postupům ještě přidat pohrávání si s Implied Volatiltou? Pravděpodobně to možné je a základním předpokladem by pak mohlo být dokonalejší poznání chování samotné Implied Volatility a porozumění jejich základních vlastností. Nebudu k tomu používat žádné složité výpočty nebo rozebírat složité matematické vzorce, od toho tady jsou akademické studie a odborná literatura, budu se snažit využít to, co je mi nabízeno prostřednictvím dostupného software tak, abych si mohl o Implied Volatilitě udělat nějaký vlastní obrázek a tento náhled pak možná přenést do nějaké obchodní reality.
Volatility Skew
Výpočet ceny opce podle oceňovacího modelu je asi pochopitelná věc, musí se jednoduše výpočtem stanovit, jaká je cena opce a tuto cenu pak prezentovat jako nabídku pro uzavření nějakého obchodu s určitým typem opčního kontraktu. V článku Cena opce jsem popisoval, jakým způsobem se cena opčního kontraktu může vypočítat podle Black-Scholesova modelu a které veličiny do tohoto výpočtu vstupují. Pro oprášení znalostí je cena opce tvořena Cenou podkladu, Hodnotou Strike, Dobou do expirace, aktuální Úrokovou mírou, hodnotou vyplácené Dividendy a Implied Volatilitou. Tyto cenotvorné prvky vstupují do matematického modelu, aby jeho výstupem byla cena opčního kontraktu. V teoretickém světě by pak z tohoto jednoduchého popisku cenotvorby mělo vyplývat, že by ceny opcí měly být pro každý strike a v každé expiraci lehce vypočitatelné, protože by se jednalo o výlučně matematickou operaci. V reálném světě tomu tak samozřejmě není, protože na ceny opcí působí velmi mnoho tržních vlivů, které se formují do nabídky a poptávky po jednotlivých opčních kontraktech a tyto tržní tlaky způsobují deformaci cen jednotlivých opčních kontraktů. Jednoduše jsou někteří účastníci trhu ochotni za určitý opční kontrakt zaplatit více než za jiný a mohou pro to mít spoustu racionálních důvodů. Spekulativní nákupy, očekávané fundamentální události, negativní ekonomické a politické nálady, insider informace a já nevím co dalšího působí na cenu opčních kontraktů a způsobuje deformaci jejich cen. V principu opční cenotvorby pak musím vyhodnotit, že pokud jsou hodnoty položek – Cena podkladu, Hodnota Strike, Doba do expirace, aktuální Úroková míra a hodnota vyplácené Dividendy v každém okamžiku stálé, poznatelné a jednoznačně dané, tak se ceny opčních kontraktů, které mají jinou strukturu něž tu, kterou vypočítal nějaký matematický model, musí lišit o hodnotu Implied Volatility. Implied Volatilita je tak jedinou proměnnou, která bude, pod tlakem nabídky a poptávky po opcích na jednotlivých strike a v jednotlivých expiracích, mít odlišné hodnoty. Takto strukturovaná Implied Volatilita pak bude vytvářet nejrůznější stavy, které budou patrné v jednotlivých opčních řetězcích a v jednotlivých expiracích a tato struktura pak může mnoho napovídat o struktuře daného trhu, fundamentální náladě a samotné obchodní aktivitě. Pokud se liší cena opčních kontraktů na různých strike a v různých expiracích, bude patrně struktura Implied Volatility vytvářet podle těchto svých strike a expirací různě sešikmené a tvarované křivky – křivky znázorňující tzv. Volatility Skew (šikmost). Zkoumání tvarů těchto křivek pak může nabízet velmi dobré interpretace a zajímavé pohledy na konkrétní trhy.
Je velmi nepřehledné a nekomfortní vyhodnocovat aktuální hodnoty Implied Volatility na jednotlivých strike a v jednotlivých expiracích přímo z opčního řetězce v obchodní platformě. „Skewness“ (šikmost) Implied Volatility mohu u svého brokera vyhodnocovat graficky v nejrůznějších zobrazeních a bylo by s podivem, kdyby některý z opčních brokerů takové grafické interpretace nenabízel. Jsem klientem Interactive Brokers, předpokládám, že drtivá většina čtenářů také, proto se zaměřím na grafické znázornění Volatility Skew právě pomocí jeho obchodní platformy TWS. Předpokládám také, že pokud jiní opční brokeři nabízejí pohledy na křivky Implied Volatility, budou nabízet klientům obdobné pohledy sestavené na obdobných principech.
Volatility Smile a Volatility Smirk
Pokud se pohybuji na půdoryse představy, že pro výpočet opčních cen na jednotlivých strike a v jednotlivých expiracích použiji Black-Scholesův oceňovací model, tak mohu zjistit, že tak, jak jsem postupoval při výpočtu Historické Volatility v tomto článku, mohu aplikovat svůj teoretický pohled na ceny opcí na jednotlivých strike obdobným způsobem. Vztah mezi cenou podkladu a cenou jednotlivého strike mohu vyjádřit jako přirozený logaritmus (ln) podílu ceny strike a aktuální ceny a současně pohyb podkladu v čase si mohu nechat popsat (v intencích Black-Scholesova modelu) jeho druhou odmocninou. Mohu potom vyjádřit očekávání pohybu podkladu od aktuální ceny k ceně strike jako přirozený logaritmus podílu ceny strike a aktuální ceny vydělený druhou odmocninou času, pro který tento pohyb sleduji. Takový postup by pak mohl představovat velmi jednoduchou představu očekávání pohybu k jednotlivým strike v daném čase a zobrazoval by precizní údaje podle tohoto oceňovacího modelu očištěný o jakékoliv tržní vlivy. Na obrázku níže je příklad takového teoretického výpočtu pro jednotlivé strike na akcii AAPL, která se obchoduje v danou chvíli za 235,28 USD a představuje velmi zjednodušený pohled na tvar Volatility Skew na jednotlivých cenách podkladového aktiva.
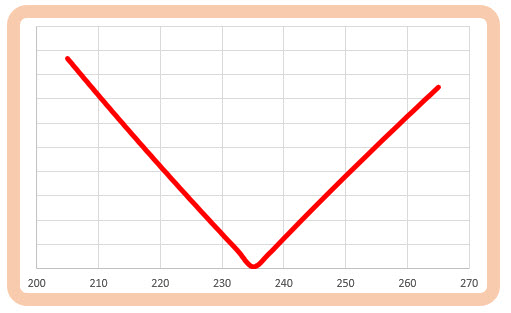
V „laboratorních podmínkách“ by pak křivka skew mohla vykazovat například takový ideální tvar. Svět ale není mexická telenovela, proto je samozřejmé, že na tyto ideální tvary budou působit tržní vlivy nabídky a poptávky a také je jasné, že tvůrci cen nebo obecně účastníci trhů disponují sofistikovanějšími modely než je ten klasický Black-Scholesův. Tvar této křivky tak bude zcela jistě nejméně z těchto důvodů deformován. Jak vypadá taková ideální křivka po deformaci vnějšími vlivy si mohu nechat zobrazit v nějakém jednoduchém analytickém nástroji. V mém případě, pro pochopení významu znázorňované struktury křivky Implied Volatility, mohu použít níže uvedený obrázek, který mohu vyvolat v platformě TWS mého brokera, a to z tohoto umístění TWS/Analytical Tools/Option Analysis/Volatility Skew, abych získal grafické zobrazení jako na níže uvedeném obrázku.
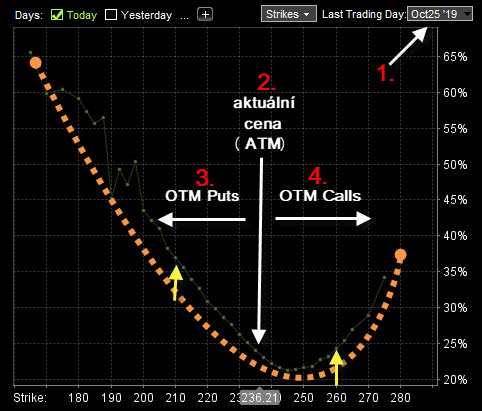
Na obrázku je vyobrazena aktuální křivka Implied Volatility na jednotlivých strike podkladové akcie AAPL pro opční řetězec expirující 25.10.2019 (tlustě tečkovanou křivku jsem dodal pro větší názornost). Volbu opčního řetězce (expirace) mohu vykonávat pomocí rolovacího menu označeného (1). Co tedy mohu z obrázku odezírat? Na ose „x“ mám možnost pozorovat jednotlivé strike podle ceny podkladu s vyznačením aktuální ceny podkladu v danou chvíli (2). Na ose „y“ jsou pak vyneseny hodnoty Implied Volatility pro jednotlivé opční strike, které jsou „mimo peníze“. Na grafu v jeho levé části jsou na ose „y“ vyneseny hodnoty Implied Volatility pro strike, které leží pod aktuální cenou, tedy OTM Put opční kontrakty (3) a na grafu v jeho pravé části jsou na ose „y“ vyneseny hodnoty Implied Volatility pro strike, které leží nad aktuální cenou, tedy OTM Call opční kontrakty (4). Jednoznačně mám možnost pozorovat, že křivka Implied Volatility se na mě „jaksi směje“ s „mírně přidrzlým“ povytaženým levým koutkem. Zkoumání „úsměvu“ a „míry jeho drzosti“ může nabízet zajímavé informace. Na obrázku výše jsem pak vyznačil dvě situace malými žlutými šipkami, které mohu vysvětlit obrázkem níže.
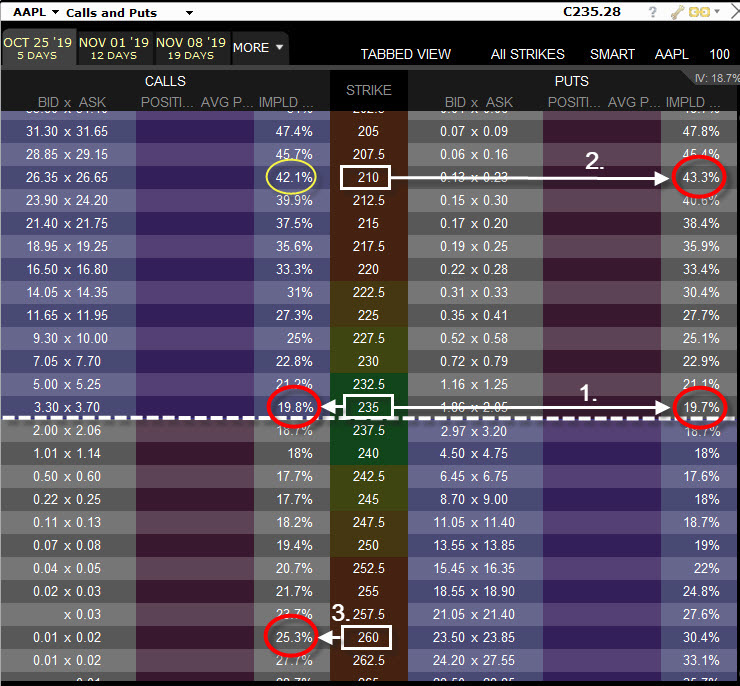
První patrná vlastnost Implied Volatility, která stojí za zaznamenání, je souvislost velikosti Implied Volatility na Call i Put opci na stejném strike, vyobrazená jako případ (1). Je patrné, že hodnoty Implied Volatility pro Call opci i Put opci na stejném strike jsou si velmi podobné a nevykazují zásadní odlišnosti, tyto se projevují (velmi vlažně), jak se opční strike ponořují „do peněz“, tedy vzdalují od aktuální ceny a od ATM strike (v obou směrech), bude mi tak nyní stačit konstatování, že hodnoty Implied Volatility pro Call i Put opce na stejném strike jsou přibližně stejné. Proč tomu tak je? Pokud by existoval zjevný nepoměr mezi hodnotou Implied Volatility na stejném strike pro opční kontrakt Call i Put, vytvářely by se bezrizikové obchodní příležitosti, jednoduše by to znamenalo, že opční kontrakt z vyšší Implied Volatilitou by měl vyšší cenu než stejný opční kontrakt na stejném strike a byl by tak výrazně předražen oproti ceně opčního kontraktu s Implied Volatilitou nižší. Stačilo by pouze dražší opční kontrakt prodat a nakoupit kontrakt levnější současně s pořízením podkladového aktiva (vytvořit Delta Neutral pozici) a uzamknout profit do Conversion nebo Reversal. Stejné a vyvážené hodnoty Implied Volatility pak udržují svými obchody tradeři, kteří se snaží z takových malých rozdílů opravdu těžit (například tvůrci trhů). Z důvodu této vytvořené rovnováhy hodnoty Implied Volatility na stejném strike pro Call i Put opční kontrakty, jsou na ose „y“ těchto grafů vyneseny hodnoty Implied Volatility pro opční kontrakty „mimo peníze“, protože se předpokládá, že hodnoty opčních kontraktů na stejném strike „v penězích“ by měly být stejné. Mohu tak pro potvrzení této skutečnosti z obrázku výše vypozorovat, že Implied Volatilita na strike Long Put 210 je na hodnotě 43,30% (2) a hodnota Implied Volatility opčního kontraktu Long Call 210 (žlutý kroužek) je na hodnotě 42,10%, když tato opce je silně ponořena „v penězích“ a neměla by tak být vůči stejnému opčnímu kontraktu na stejném strike „předražena“ a nenabízí proto žádnou příležitost k jednoduché arbitráži.
Je ale z obrázku patrné, že z tvaru křivky Volatility Skew vyplývá, že nejsou v žádném případě stejné hodnoty Implied Volatility na strike stejně vzdálených od aktuální ceny podkladového aktiva. Tato se při pořízení obrázku výše obchodovala okolo 235 USD, a proto jsem do grafu výše vyznačil žlutými šipkami hodnoty Implied Volatility pro strike ve vzdálenostech +/-25 USD od této současné ceny a také tyto hodnoty jsem vyznačil do obrázku opčního řetězce z platformy TWS. Je zřetelné, že na straně Put, na strike 210 vzdáleném -25 USD od aktuální ceny atakuje Implied Volatilita hodnotu 40% (2), kdežto na straně Call, na strike 260 vzdáleném +25 USD od aktuální ceny dosahuje hodnota Implied Volatility hodnotu kolem 25% (3), To je obrovský rozdíl a představuje značných 15%. Mohu tak pozorovat, že hodnoty Implied Volatility jsou daleko vyšší na levé straně grafu, proto se mi křivka „šikmosti“ Implied Volatility vytvoří právě ve tvaru úsměvu s povytaženým levým koutkem.
Tato formace křivky je typická například pro akciové tituly. Způsobuje ji vyšší poptávka po Put opcích „mimo peníze“, které slouží k zajišťování držených akciových pozic, jako odraz existence obecného pocitu bolesti z pádů akciových trhů a snahy být na takové poklesy připraven. Pokud bych vyšel z interpretace, že hodnota Implied Volatility je stejná na Call i Put straně, pak se zdá, že jsou vyšší také ceny Call opcí, které jsou svými strike aktuálně „v penězích“ a mohlo by to také znamenat, že substituovat akciové pozice hluboce ITM Call opcemi se nyní opravdu může dít. Simulovat držení podkladu Long Call opcemi hluboce „v penězích“ má výhodu v omezeném risku (nemohu prodělat více než její pořizovací cenu) a také „pákový efekt“ vyplývající z výhody držení takové opce namísto přímé akciové pozice. Obrázek s křivkou „úsměvu“ tak odhaluje míru vyšších tržních tlaků vyplývající z nabídky a poptávky po určitých typech opčních kontraktů (zejména na Put straně na strike „mimo peníze“), které se projevují do růstu hodnot Implied Volatility na těchto jednotlivých strike, které takovými tržními nápory trpí (tedy levá strana křivky). Tento tvar také mohu jednodušeji interpretovat jako obecný názor opčních obchodníků na pohled na akciové trhy, na kterých se se svými opčními kontrakty pohybují, a sice, že tyto akciové trhy rády rychleji spadnou, než by se stejnou rychlostí rostly.
Zobrazování křivek Implied Volatility Skew může být užitečným pomocníkem, jak pohlížet na nálady držitelů opčních kontraktů ve spojitosti s očekáváním trhů. Mohu se pak zabývat pozorováním deformací této křivky a z nich vytvářet vlastní obchodní úsudky nebo vytvářet obecné i konkrétní náhledy na konkrétní trhy. Toto mi může u mého brokera umožnit volba analytické aplikace Multi-Expiry Skew z umístění TWS/Analytical Tools/Option Analysis/Volatility Skew/Multi-Expiry Skew.
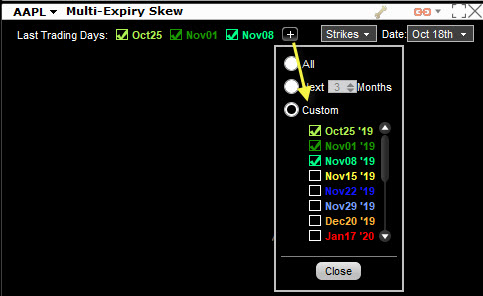
Po zadání výběru tickeru podkladového aktiva (například AAPL) si mohu z rozbalovacího menu vybrat, které opční řetězce si podle své expirace mohu nechat zobrazit, abych si mohl prohlédnout, jak vypadá rozložení Implied Volatility například (podle obrázku výše) v nejbližších třech expiracích. Proč bych měl takové „multiexpirační“ zobrazení vlastně zadávat? Stejně jako se vytváří „šikmost“ díky nestejným hodnotám Implied Volatility na různých strike ve stejné expiraci – Vertical Skew, tak mohu také pozorovat „“šikmost“ Implied Volatility na stejných strike, ale v různých expiracích – Horizontal Skew. Na obrázku níže je obrázek s nejbližšími dvěma expiracemi pro titul KSU.
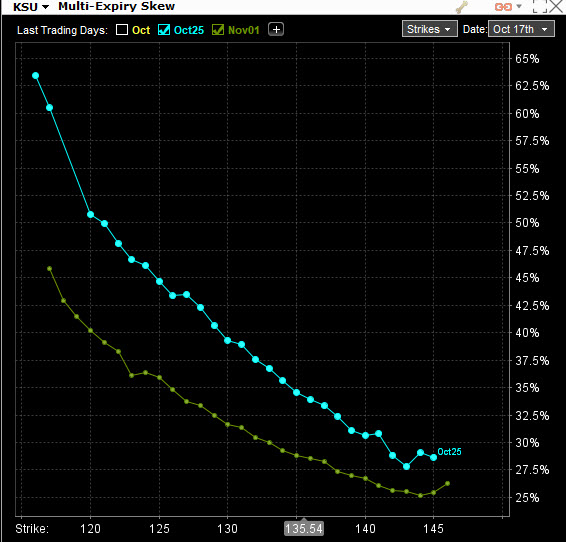
V pátek 18.10.2019 vyhlašovala společnost KSU hospodářské výsledky a je více než patrné, jaké byly obavy investorů do akcií KSU prostřednictvím pořizování opčních kontraktů. Tlak na strike na levé straně grafu způsobený poptávkou po OTM Put opcích zdeformoval hodnoty Implied Volatility tak, že se „úsměv“ nakonec změnil v „úšklebek“ (Smirk). Není ale jednoduché dělat z pohledu na takto tvarované skew nějaké jednoznačné závěry, protože to také může jednoduše jen znamenat, že tento akciový titul jenom nemá vysokou opční likviditu a investoři do akciových titulů se pouze zajišťují proti propadu před Earnings a nemají v danou chvíli zájem na tomto titulu vytvářet opční struktury participujících na případném uptrendu vytvořené z Call opčních kontraktů. KSU je akciový titul, kde velké podíly drží institucionální investoři a velké investiční fondy s Long akciovými pozicemi, což by mohlo takové tvarování skew vysvětlovat. Pozoruhodný je ale také pohled na rozdíly mezi hodnotami Implied Volatility na stejných strike, ale v těchto dvou zobrazených rozdílných expiracích (Horizontal Skew). Je patrné, že obě křivky jsou od sebe výrazně odděleny, když křivka Skew s nejbližší expirací je výrazně výše na všech cenových úrovních pro všechny strike. Pro ilustraci a srovnání je na dalším obrázku zobrazeno „předEarnings“ očekávání obchodníků na akciovém titulu TSLA.
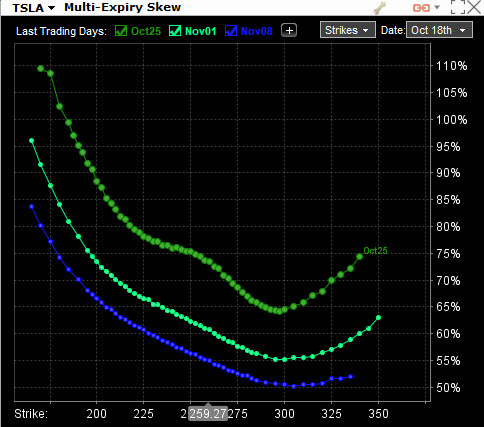
Tesla reportuje své výsledky 23.10.2019, tedy v expiraci opčního řetězce, který je nejvýše položenou křivkou a která odpovídá nejvyšším hodnotám Implied Volatility. Na nějaký velký smích to tedy rozhodně nevypadá… :c). Přestože je patrné, že na křivce skew pro tuto nejbližší expiraci je velký tlak na Put opce „mimo peníze“ a křivka vykazuje protažení a sešikmení na levé straně grafu, je patrné, že zcela pozadu nezůstali ani obchodníci, kteří se rozhodli spekulovat na pravé straně obrázku, tedy s Call opčními kontrakty. TSLA je samozřejmě předmětem daleko větší pozornosti opčních obchodníků než nudná železniční akcie KSU s velmi malým opčním Volume a Open Interest, proto je rozložení pozornosti na jednotlivé strike také výrazně pestřejší. Opět je také patrné značně široké Horizontal Skew, kde křivky pro jednotlivé za sebou jdoucí expirace jsou poskládány od nejvýše položené k nižší. To u Goldmanů (GS) mají již po významné fundamentální zprávě (vyhlášení hospodářských výsledků), proto se může Implied Volatilita na jednotlivých strike uvolnit do svých běžnějších hodnot, aby vykreslovala běžný pohled na její rozložení v jednotlivých opčních expiracích, které jsem do aplikace zadal a nechal si zobrazit podle níže uvedeného obrázku.
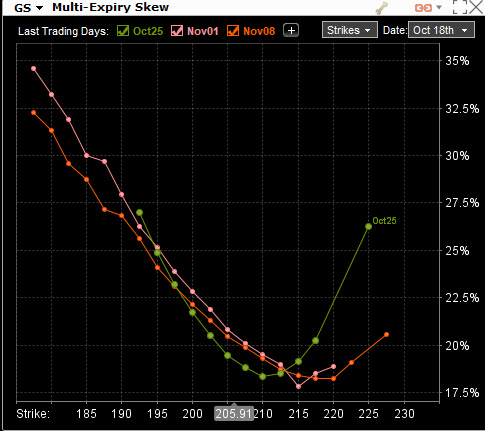
Mohu pozorovat běžný a ničím neobvyklý tvar Volatility Smile pro Vertical Skew, tedy pro opce se stejnou expirací. Pro akciové tituly vyšší poptávka po Put opcích tvořících úsměv s povytaženým koutkem na levé straně grafu. Co je ale výrazně jiné, než na předchozích obrázcích se značně diferencovanou Implied Volatilitou v jednotlivých expiracích, je téměř vymizení pozorovatelně významnějšího Horizontal Skew. GS nemá před sebou žádnou významnou fundamentální zprávu, která by se projevila zvýšením hodnoty Implied Volatility na strike s expirací nejblíže po jejím vyhlášení a mohu pozorovat, že ve třech po sobě jdoucích expiracích, které reprezentují zobrazené křivky, jsou hodnoty Implied Volatility na stejných strike v těchto různých expiracích (zejména na levé straně obrázku) výrazně podobné.
Co je vlastní akciovým titulům, neplatí pro jiné třídy aktiv, které mohu obchodovat a používat přitom opční kontrakty. Volatility Skew a tvary její křivky, které mohu odůvodnit náladami opčních investorů, vyplývají ze samotné podstaty těchto podkladových aktiv. V minulém příspěvku jsem popisoval Delta Neutral obchod na prosincové kukuřici a zmínil se přitom, že Implied Volatilita se mění za jiných podmínek a jiným způsobem, než jsem zvyklý u akciových titulů, toto pak obecně platí pro všechny zrninové kontrakty. Na obrázku níže je vyobrazeno rozložení Implied Volatility na jednotlivých strike pro opční kontrakty s prosincovou a únorovou expirací pro podkladové futures – pšenici s dodáním v březnu 2020.
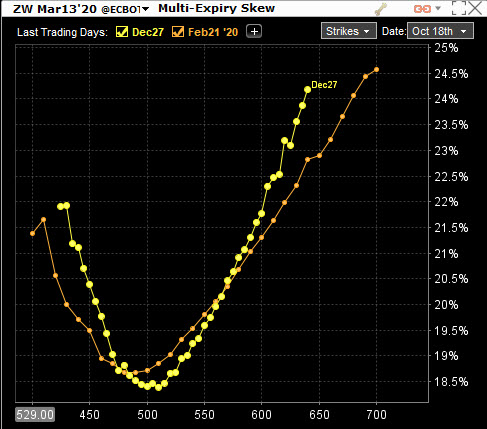
Úsměv ano, přidrzlost také, ale drzost je nyní znázorněna naopak povytažením pravého koutku pomyslného úsměvu Volatility Skew. Tento typický pohled je vlastní zrninám z důvodu obav o explozi ceny podkladové komodity, způsobené například nepřízní počasí, nízkými výnosy sklizně, ohrožením export/importu, klesajícími zásobami…. Hledání zajištění se tak přesouvá na Call stranu a zvyšuje poptávku po Call opcích jako participaci na uptrendu vyplývajícího z těchto nepříjemných fundamentů.
Zajímavý pohled by se mohl také naskýtat na tvar Volatility Skew pro opční řetězce VIX.
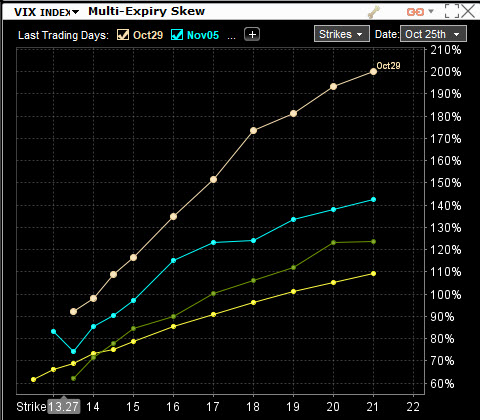
Není asi zapotřebí velkého komentáře k obavám, které formují nabídku a poptávku po VIX opčních kontraktech, veškerá pozornost se soustřeďuje na Call stranu grafu zcela jasného „úšklebku“ Volatility Skew a může popisovat základní vlastnost chování VX futures – raketově nabývat na své ceně při tržních otřesech na trzích měřených indexem S&P 500. Za povšimnutí stojí popisky na ose „y“, které reprezentují Volatilitu Volatility popisovanou v tomto článku. Spekulace s VIX opcemi se tak dějí převážně na Call straně opčních řetězců a z tvarů křivek Implied Volatility na jednotlivých strike tak jednoznačně vyplývá, že Call opční kontrakty v určité vzdálenosti od současné ceny podkladu mají daleko vyšší hodnotu než stejně vzdálené Put opční kontrakty. Pokud již vím, že hodnota VIX Indexu má obvyklou hodnotu neklesající pod 10 bodů a v obrázku pak mohu pozorovat, že aktuální hodnota spotové ceny se nachází okolo třinácti bodů, nebudou Put opční kontrakty, které jsou „mimo peníze“, stát nějaké dramatické peníze a nebudou patrně předmětem nějaké zvýšené obchodní pozornosti. Za upozornění stojí také výrazně vykreslené Horizontal Skew, kdy jednotlivé křivky jsou podle expirací od sebe velmi zřetelně odděleny.
Volatility Skew – zobrazení v čase
Přestože si každý z analytiků, traderů, autorů nebo mentorů nazve pozorované tvary jednotlivých křivek šikmosti Implied Volatility na různých strike a v různých expiracích po svém (Positive Skew, Negative Skew, Reverse Skew…), pro všechno názvosloví existují dva společné jmenovatele. Hodnoty Implied Volatility se liší na jednotlivých strike pro opční řetězec ve stejné expiraci (Vertikální Skew) a také se liší na stejných strike pro různé expirace (Horizontal Skew). To, že se Implied Volatilita mění v dané expiraci podle svých strike a co ji způsobuje je již popsáno výše. Pozorování křivky Implied Volatility na jednotlivých strike pak vykreslí její tvar pro daný strike a danou cenu v aktuální chvíli a mohu pak pozorovat její konkrétní tvar. Tento Vertical Skew a Horizontal Skew se však v čase neustále vyvíjí a mění. Je to proto, současně s běžícím časem se mění tržní vlivy a z něj vyplývající změny nabídky a poptávky. Tyto jednotlivé změny by patrně nebylo špatné pozorovat a také podrobit nějakému zevrubnému vyhodnocování. Takovou možnost mi analytická část aplikace TWS také nabízí pro pozorování časového vývoje Vertical Skew. Na obrázku níže je možnost takové volby například pro e-mini S&P 500 prosincové futures (ES).
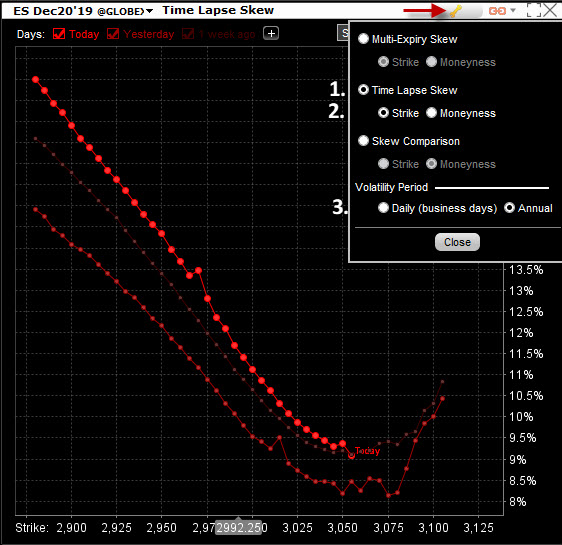
V analytické platformě TWS/Analytical Tools/Option Anylysis/Volatility Skew vyberu možnost „Time Lapse Skew“. Poté si vyvolám nabídku úpravy skrytou pod ikonou klíče (červená šipka). Potvrdím tlačítkem volbu „Time Lapse Skew“ (1) a vyberu možnost „Strike“ (2). Tímto zadám zobrazování jednotlivých strike na ose „x“ namísto procentního údaje, nakolik je daná cena na ose „x“ v penězích (alternativní volba „Moneyness“). Dále potvrdím volbu „Annual“ (3), kterou si na ose „y“ navolím hodnoty Implied Volatility v ročním procentním tvaru namísto jejího denního vyjádření (přepínání je ale skvělý pomocník, jak roční Implied Volatilitu „odannualizovat“ na denní bázi). Takto připravený graf mohu dále upravit o znázornění jednotlivých křivek průběhů Implied Volatility v historii.
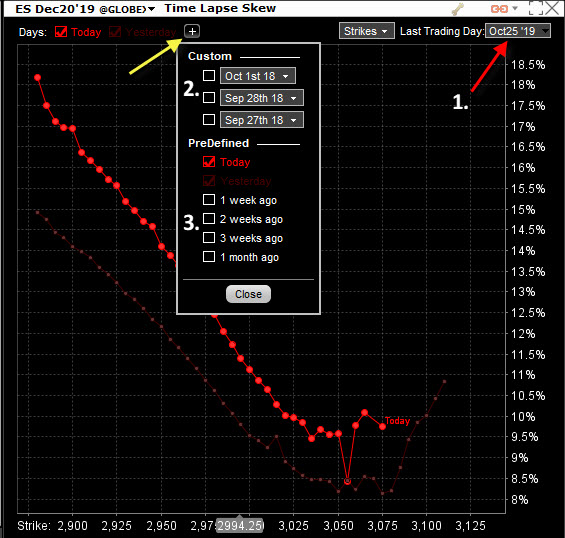
Z nabídky označené červenou šipkou (1) si vyberu, která opční série (podle data expirace) mě bude při zobrazení zajímat, v mém konkrétním případě si chci nechat zobrazovat tvar křivky Implied Volatility pro jednotlivé strike v opčním řetězci s expirací 25. října 2019. Kliknutí na rozbalovací menu označené žlutou šipkou mohu vybírat z historie, který okamžik bych si k současnému zobrazení křivky mohl přidat a vypozorovat pohyb Implied Volatility. Mohu vybírat z přesně stanovených termínů podle mé volby (2) nebo mohu využít předdefinované historické časy volbou podle (3). V mém případě jsem chtěl k dnešnímu aktuálnímu pohledu přidat včerejší křivku hodnot Implied Volatility na jednotlivých strike.
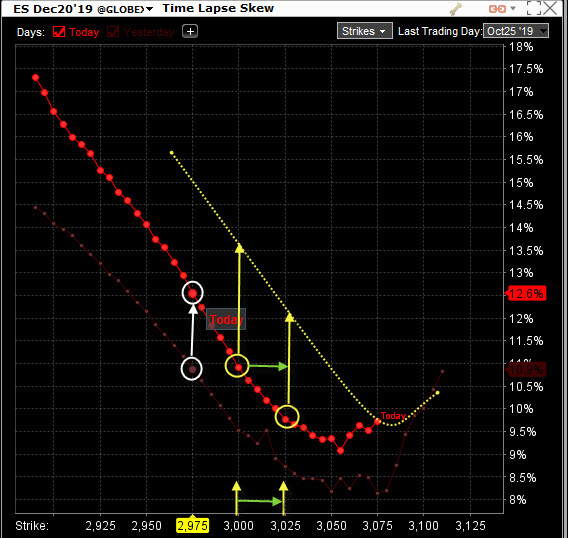
Mohu vypozorovat, že se křivka s dnešním průběhem nepohnula (podle svého dna) ani doprava ani doleva oproti průběhu minulého obchodního dne (grafické znázornění včerejšího průběhu ve formě níže položené velmi mdlé červené slabší křivky je výplodem analytického nástroje a nemůžu jej ovlivnit), toto je způsobeno zejména situací, že se nezměnila cena podkladového futures, protože se nyní obchoduje za téměř stejnou cenu jako k předcházejícímu Close. Křivka dnešního průběhu se však posunula zřetelněji výše a znamená to zvýšení Implied Volatility na jednotlivých strike oproti včerejšku. Také mohu pozorovat větší „sevření křivky“ a zvýšení „šikmosti“ na levé straně grafu, což mohu interpretovat, že zvýšení Implied Volatility je vyšší na vzdálenějších než na bližších strike vzhledem k aktuální ceně obchodovaného futures. Velikost Implied Volatility se na těchto vzdálenějších strike zvětšila a „více roztáhla“ a vytvořila sice velmi nepatrné, ale větší vzdálenosti mezi sousedními OTM Put strike. Pro srovnání jsem v obrázku křivek označil hodnoty na strike 2975 bílými kroužky a bílou šipkou, kdy pro opční kontrakty na tento strike s expirací 25.10.2019 vystoupala mezidenně hodnota Implied Volatility z úrovně 10.90% na hladinu 12.60%.
Tento efekt zachování přibližného tvaru křivky včerejšího skew a dnešního skew mohu také využít k extrapolaci hodnoty Implied Volatility při určitém pohybu podkladového aktiva. Do obrázku jsem přidal žlutě tečkovanou fiktivní křivku, která by mohla znázorňovat uptrend podkladového futures, který jsem znázornil zelenými vodorovnými šipkami. Mohu pak pozorovat, jak se velmi výrazně změní Implied Volatilita na jednotlivých vybraných strike 3000 a 3025, pokud připustím, že tvar křivky zůstane víceméně zachován.
Pro analytické pozorování křivky Volatility Skew mohu v aplikaci TWS vyvolat také nabídku 3D zobrazení pro vybraný titul a pozorovat současně tvary jednotlivých křivek Volatility Skew pro jednotlivé expirace na jednotlivých strike. Mohu tak současně nahlížet na Vertical Skew a Horizontal Skew. V platformě TWS pak mohu k otevření 3D zobrazení využít tuto cestu TWS/Analytical Tools/Option Anylysis/Interactive Analytics/3D Volatility Surface. Zvolením podkladového aktiva je incializováno otevření stránky prohlížeče s vyobrazením 3D Volatility Skew. Na obrázku níže například pro titul GS.
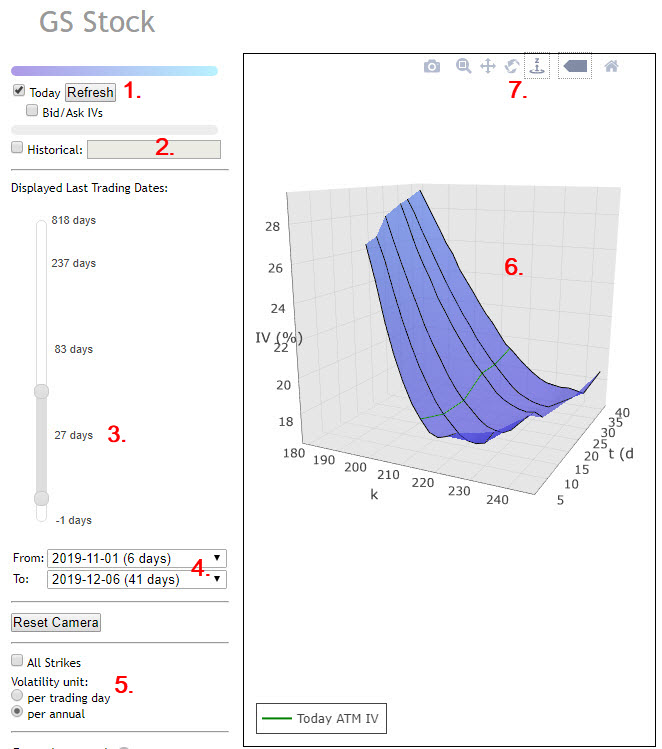
Zobrazení poskytuje nejrůznější volby. Mohu si nechat zobrazovat aktuální situaci (1) nebo se také podívat do nějakého časového bodu v historii (2). Na posuvníku (3) mohu tažením vybírat zobrazování jednotlivých expirací, stejně tak mohu toto časové rozpětí zadat výběrem (4). Mohu také přepínat mezi zobrazením hodnoty denní Implied Volatility nebo roční Implied Volatility (5). Na ploše grafu (6) pak mohu na jednotlivých osách 3D modelu pozorovat jednotlivé hodnoty Na ose „x“ jsou jednotlivé strike, na ose „y“ je znázorněná Implied Volatilita na těchto strike a na ose „z“ jsou jednotlivé expirace a k nim odpovídající Implied Volatilita na jednotlivých strike. Svisle vedené černé čáry v modré ploše grafu pak ukazují na jednotlivé expirace, tenká zelená čára vedoucí napříč grafem zobrazuje aktuální Implied Volatilitu na ATM strike pro každou ze zobrazovaných expirací. K dispozici jsou pak další zobrazovací nástroje (7). Mohu pak vypozorovat, jak se Implied Volatilita na jednotlivých strike „rozlévá“ do budoucnosti jako rozšiřující se koryto řeky se stále mělčí hladinou vody v něm, což zobrazuje nejběžnější stav průběhu Implied Volatility na jednotlivých strike pro akciový titul ve smyslu Vertical Skew a Horizontal Skew. Pomyslné koryto řeky Implied Volatility pak má patrný vyšší levý břeh (větší zájem o Put opční kontrakty) a mírnou svažitost po jejím pomyslném proudu směrem do budoucnosti. Obrázek je silně zmenšený pro potřeby tohoto článku, při jeho zobrazení na celé ploše displeje počítače jsou pak tyto vlastnosti velmi plasticky vyvedeny a dobře pozorovatelné.
Pro srovnání na obrázku níže aktuální 3D model Implied Volatility Skew pro akcii Facebook (FB).
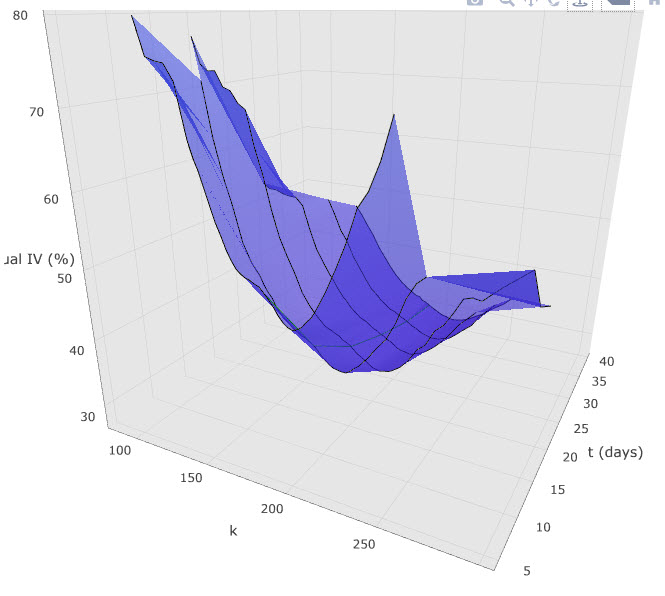
Pomyslná řeka vytvořená 3D projekcí Implied Volatility Skew vyhloubila směrem do budoucnosti zatraceně hluboké koryto, které u „svého pramene“ (dnešní den) má opravdu hluboký průběh. Není to způsobeno ničím jiným než skutečností, že v době do expirace prvního opčního řetězce v pořadí (1.11.2019) probíhá vyhlašování hospodářských výsledků (30.10.2019). Kromě hloubky jednotlivých křivek vytvarované pomocí Vertical Skew pak mohu také pozorovat značnou šířku jednotlivých podélných modrých pásů grafu (zejména prvních dvou) oddělených černými hraničními křivkami jednotlivých expirací, které zobrazují značně veliké (široké) Horizontal Skew, vytvořené vysokými hodnotami Implied Volatility na obdobných strike v prvních dvou expiracích. Další modré pásy více v budoucnosti pak již mají tyto své šířky menší a do budoucnosti se tak zužují a zobrazují předpoklad, že se očekávaná volatilita na vzdálenějších expiracích bude vracet do normálu. Pro lepší vyhodnocení tohoto Horizontal Skew mohu provádět natáčení grafu podle své potřeby přichycením a tažením myší v ploše grafu. Mohu si tak tento 3D model otočit „více zboku“ a pozorovat například právě zmiňované Horizontal Skew.
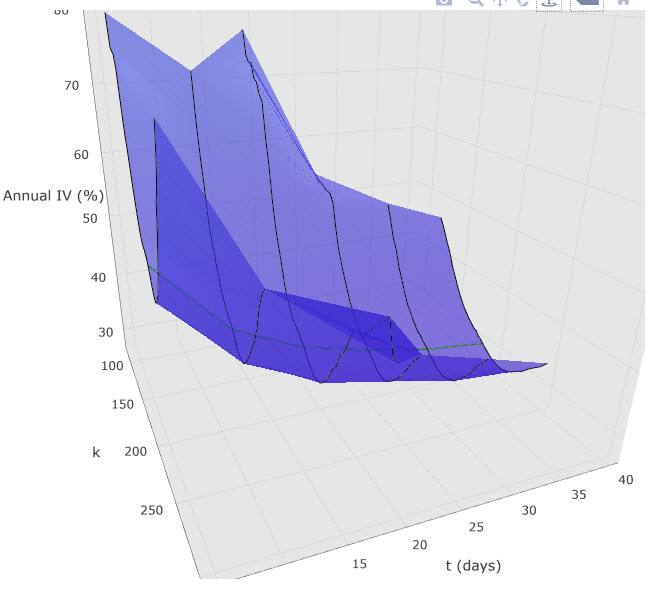
Každý si může interpretovat pohled na Volatility Skew svým způsobem, patrně jinak se na něj bude dívat tvůrce trhu, jinou optikou na něj bude nahlížet multimilionový investiční fond a zcela jiný úsudek si vytvoří běžný opční trader. Bez pohledu na křivku Volatility Skew se dá určitě v běžném obchodním životě existovat a nemusím se jejím nepochopením výrazně trápit. Mě osobně zajímá, jak si můžu takovou vlastnost Implied Volatility převést do reálného obchodního rozhodnutí a řečeno velmi zjednodušeně – jak ji „přetavit na peníze“. Zdálo by se, že pokud by se mi to nedařilo, je toto poznání pravděpodobně k ničemu. Nemusí to být ale pravda, právě toto poznání může být významným střípkem do mozaiky celkového názoru na nějaký skvělý obchod nebo může podpořit jiné argumenty pro chystané obchodní rozhodnutí. Článek byl malým teoretickým vhledem do problematiky Implied Volatility a pozorování její úrovně na různých strike a v různých expiracích pomocí jednoduchých a dostupných grafických pomůcek. Na tento článek se pak pokusím navázat zcela praktickou ukázkou obchodů, které ve své podstatě využívají poznané vlastnosti Implied Volatility a vycházejí z principů Delta Neutrality :c)
Komentáře a příspěvky prosím směrujte do Diskuzního fóra do tohoto vlákna :c)
Sleduj facebook, napiš e-mail nebo tweet

Ahoj,
stává se někdy, že se tvar těch křivek otočí, tedy že akciový skew vypadá jako zrninový nebo obráceně?
Ahoj,
na akciových trzích převažuje obava s prudkých poklesů více než obava s růstů ceny. V kombinaci s potřebou zajištění pomocí Put opcí je pak tlak na ceny Put opcí vyšší než na ceny Call opcí, takže IV vykresluje tvar skew takový, jak je popsán v článku. Mohou ale určitě nastat situace, kdy se při nějakých významných fundamentech tvar této křivky volatilit na jednotlivých strike může změnit (například nějaká dočasná vyšší poptávka po Call opcích). Stejně tak se dá na nějakých nelikvidních trzích vypozorovat, že ceny opcí jsou jakoby zcela mimo realitu, takže je možné pozorovat změnu tvaru křivky skew také z těchto důvodů…:c)